3.1.1 椭圆的简单几何性质(3)(共20张PPT)
文档属性
| 名称 | 3.1.1 椭圆的简单几何性质(3)(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
3.1.1椭圆的几何性质(3)
直线与椭圆的位置关系
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a,b,c的关系
|x|≤ a,|y|≤ b
关于x轴、y轴成轴对称;关于原点成中心对称
(a,0)、(-a,0)、(0,b)、(0,-b)
(c,0)、(-c,0)
长半轴长为a,短半轴长为b. a>b
a2=b2+c2
|x|≤ b,|y|≤ a
(b,0)、(-b,0)、(0,a)、(0,-a)
(0 , c)、(0, -c)
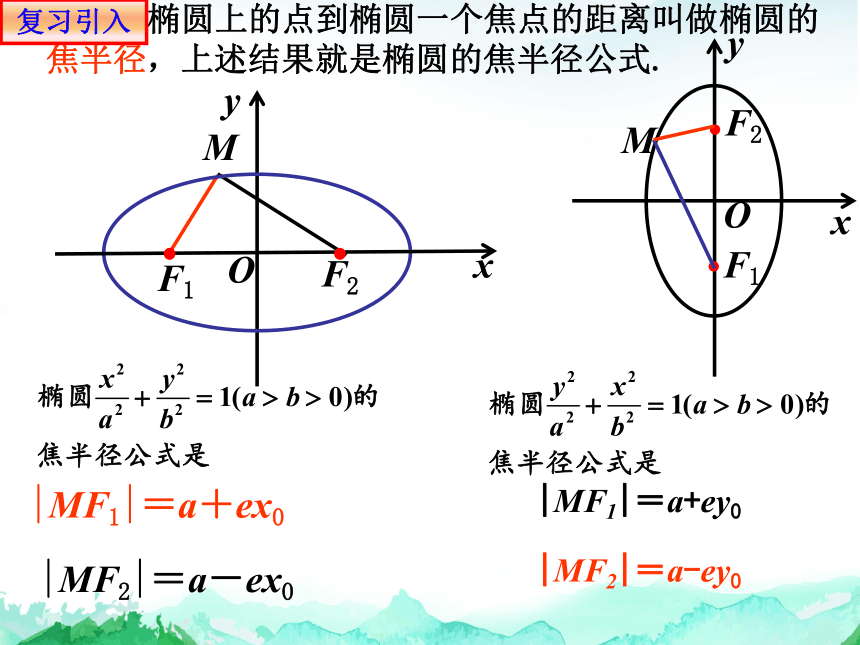
复习引入
F1
O
F2
x
y
M
椭圆上的点到椭圆一个焦点的距离叫做椭圆的焦半径,上述结果就是椭圆的焦半径公式.
|MF1|=a+ex0
|MF2|=a-ex0
|MF2|=a-ey0
|MF1|=a+ey0
x
F1
F2
y
O
M
复习引入
复习练习
复习练习
复习练习
题意:直线l:x+y-6=0到两定点的距离之和最小.
能力练习
例题讲评
典型例题
例题讲评
典型例题
课本第114页练习第1题
例2.已知椭圆5x2+9y2=45,椭圆的右焦点为F,求过点F且斜率为1的直线被椭圆截得的弦长.
典型例题
课本第114页练习第2题
韦达定理→斜率
韦达定理法:利用韦达定理及中点坐标公式来构造
椭圆中的中点弦问题
例题讲评
例题讲评
点
作差
点差法:利用端点在曲线上,坐标满足方程,作差构造出中点坐标和斜率.
例题讲评
解法三:利用对称性
弦中点问题的三种处理方法
(1)联立方程组,消去一个未知数,利用韦达定理;
(2)设两端点坐标,代入曲线方程相减可求出弦的斜率.
(3)利用对称性和中点坐标表示两端点坐标,代入方程相减.
方法小 结
1.判断直线与椭圆位置关系的方法:
解方程组消去其中一元得一元二次型方程
△< 0 相离
△= 0 相切
△> 0 相交
3 .处理弦中点问题:“点差法”、“韦达定理”
课堂小结
o
x
y
A
B
M
作业
谢谢大家
再见!
3.1.1椭圆的几何性质(3)
直线与椭圆的位置关系
标准方程
范围
对称性
顶点坐标
焦点坐标
半轴长
离心率
a,b,c的关系
|x|≤ a,|y|≤ b
关于x轴、y轴成轴对称;关于原点成中心对称
(a,0)、(-a,0)、(0,b)、(0,-b)
(c,0)、(-c,0)
长半轴长为a,短半轴长为b. a>b
a2=b2+c2
|x|≤ b,|y|≤ a
(b,0)、(-b,0)、(0,a)、(0,-a)
(0 , c)、(0, -c)
复习引入
F1
O
F2
x
y
M
椭圆上的点到椭圆一个焦点的距离叫做椭圆的焦半径,上述结果就是椭圆的焦半径公式.
|MF1|=a+ex0
|MF2|=a-ex0
|MF2|=a-ey0
|MF1|=a+ey0
x
F1
F2
y
O
M
复习引入
复习练习
复习练习
复习练习
题意:直线l:x+y-6=0到两定点的距离之和最小.
能力练习
例题讲评
典型例题
例题讲评
典型例题
课本第114页练习第1题
例2.已知椭圆5x2+9y2=45,椭圆的右焦点为F,求过点F且斜率为1的直线被椭圆截得的弦长.
典型例题
课本第114页练习第2题
韦达定理→斜率
韦达定理法:利用韦达定理及中点坐标公式来构造
椭圆中的中点弦问题
例题讲评
例题讲评
点
作差
点差法:利用端点在曲线上,坐标满足方程,作差构造出中点坐标和斜率.
例题讲评
解法三:利用对称性
弦中点问题的三种处理方法
(1)联立方程组,消去一个未知数,利用韦达定理;
(2)设两端点坐标,代入曲线方程相减可求出弦的斜率.
(3)利用对称性和中点坐标表示两端点坐标,代入方程相减.
方法小 结
1.判断直线与椭圆位置关系的方法:
解方程组消去其中一元得一元二次型方程
△< 0 相离
△= 0 相切
△> 0 相交
3 .处理弦中点问题:“点差法”、“韦达定理”
课堂小结
o
x
y
A
B
M
作业
谢谢大家
再见!
