3.2双曲线及标准方程课件(共15张PPT)
文档属性
| 名称 | 3.2双曲线及标准方程课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 11:43:22 | ||
图片预览




文档简介
(共15张PPT)
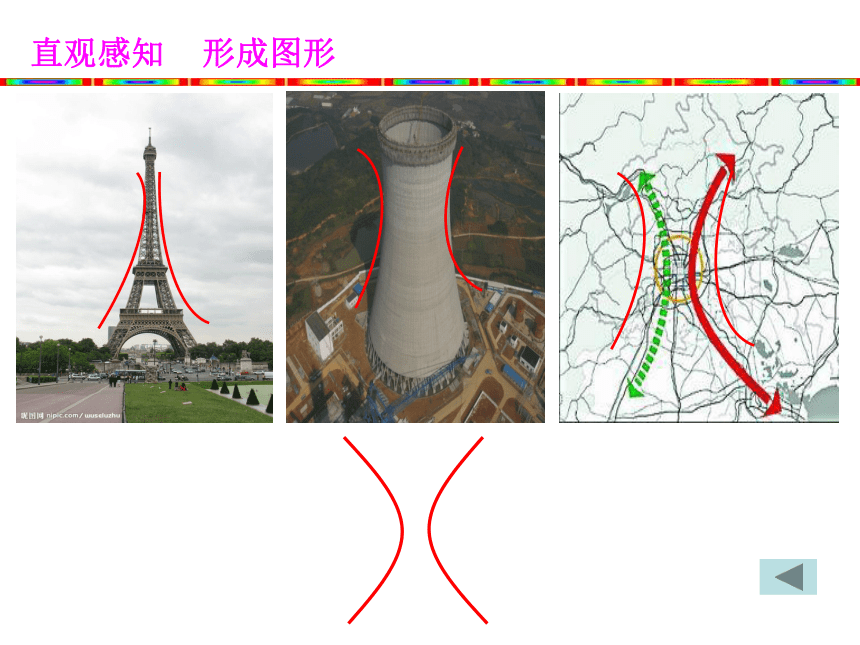
直观感知 形成图形
1、掌握双曲线的定义;
2、体验双曲线标准方程的推导过程;
3、会用待定系数法求双曲线的标准方程。
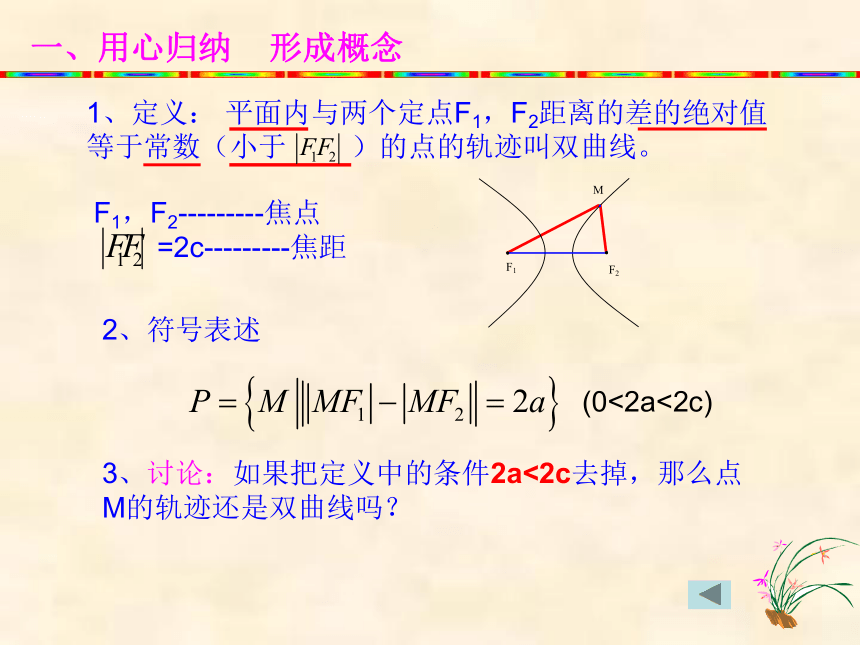
一、用心归纳 形成概念
3、讨论:如果把定义中的条件2a<2c去掉,那么点M的轨迹还是双曲线吗?
2、符号表述
(0<2a<2c)
1、定义: 平面内与两个定点F1,F2距离的差的绝对值等于常数(小于 )的点的轨迹叫双曲线。
F1,F2---------焦点
=2c---------焦距
F1
F2
M
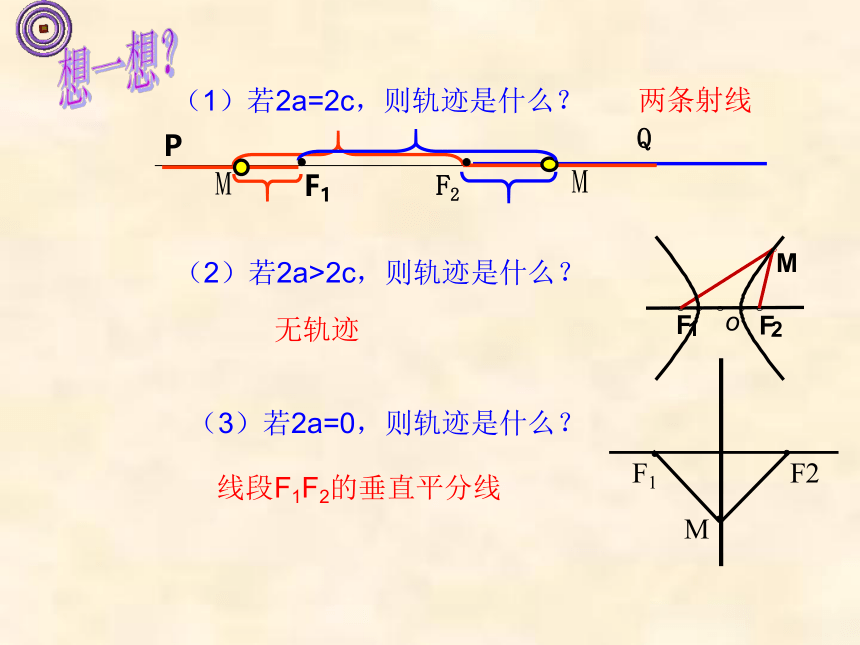
无轨迹
线段F1F2的垂直平分线
F
两条射线
F
(1)若2a=2c,则轨迹是什么?
(2)若2a>2c,则轨迹是什么?
(3)若2a=0,则轨迹是什么?
o
2
1
M
F1
F2
M
M
F2
F1
P
Q
M
口答下列各条件中点P(x,y)对应曲线的名称:
1、 F1(-2,0) F2(2,0)
2、
3、
双曲线的右支
双曲线
两条射线
当堂检测一
二、类比椭圆,推导方程
以F1、F2所在的直线为x轴,线段F1F2的中点为原点建立直角坐标系,设M(x,y),则F1(-c,0), F2(c,0),|MF1|-|MF2|=±2a
求:点M的轨迹方程
简洁,对称
1、建系 2.设点 3、列式 4、化简
三、提炼精华 总结方程
方程 叫双曲线的标准方程,
它表示的双曲线焦点在x轴上,F1(-c,0)F2(c,0),
c2=a2+b2.
F2
F1
o
x
y
思考:
当双曲线的焦点在y轴上时,它的标准方程
是怎样的呢?
x
F1
F2
o
y
双曲线 椭圆
差的绝对值 (2a<2c) 和 (2a>2c)
a>0,b>0,
但a不一定大于b a>b>0
看系数正负,右边等于1时,哪个系数正,焦点就在对应坐标轴上 通过比较分母大小来判定焦点在哪一坐标轴上
c2=a2+b2 c2=a2-b2
对比差异 深化记忆
四、典题示范,学以致用
例1 已知双曲线两个焦点分别为F1(-5,0)F2(5,0),双曲线上一点P到F1,F2距离差的绝对值等于6,求双曲线的标准方程.
解:因为双曲线的焦点在x轴上,所以设它的标准
方程为
因为2a=6,2c=10,所以a=3,c=5,所以b2=52-32=16
因此,双曲线的标准方程为
X
待定系数法
口答1、判断下列双曲线的焦点在哪个轴上,并写出焦点坐标?
口答2、已知a=4,c=5,焦点在x轴上,求双曲线的方程;
3、已知两个焦点分别为F1(0,-2)F2(0,2),且经过点
,求双曲线的方程。
(±5,0)
(0,±5 )
当堂检测二
定义
图象
方程
焦点
a.b.c 的关系
确定焦点位置
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
F ( ±c, 0) F(0, ± c)
看系数正负,右边等于1时,哪个系数正,焦点就在对应坐标轴上
五、知识入网 本节聚焦
1、知识方面:
我学到了
2、能力方面:
我学会了
3、数学方法:
我感受到了
4、还有哪些疑问
1、作业:课本P61 A组 第2题
2、探究:类比椭圆的性质探究双曲线的性质
直观感知 形成图形
1、掌握双曲线的定义;
2、体验双曲线标准方程的推导过程;
3、会用待定系数法求双曲线的标准方程。
一、用心归纳 形成概念
3、讨论:如果把定义中的条件2a<2c去掉,那么点M的轨迹还是双曲线吗?
2、符号表述
(0<2a<2c)
1、定义: 平面内与两个定点F1,F2距离的差的绝对值等于常数(小于 )的点的轨迹叫双曲线。
F1,F2---------焦点
=2c---------焦距
F1
F2
M
无轨迹
线段F1F2的垂直平分线
F
两条射线
F
(1)若2a=2c,则轨迹是什么?
(2)若2a>2c,则轨迹是什么?
(3)若2a=0,则轨迹是什么?
o
2
1
M
F1
F2
M
M
F2
F1
P
Q
M
口答下列各条件中点P(x,y)对应曲线的名称:
1、 F1(-2,0) F2(2,0)
2、
3、
双曲线的右支
双曲线
两条射线
当堂检测一
二、类比椭圆,推导方程
以F1、F2所在的直线为x轴,线段F1F2的中点为原点建立直角坐标系,设M(x,y),则F1(-c,0), F2(c,0),|MF1|-|MF2|=±2a
求:点M的轨迹方程
简洁,对称
1、建系 2.设点 3、列式 4、化简
三、提炼精华 总结方程
方程 叫双曲线的标准方程,
它表示的双曲线焦点在x轴上,F1(-c,0)F2(c,0),
c2=a2+b2.
F2
F1
o
x
y
思考:
当双曲线的焦点在y轴上时,它的标准方程
是怎样的呢?
x
F1
F2
o
y
双曲线 椭圆
差的绝对值 (2a<2c) 和 (2a>2c)
a>0,b>0,
但a不一定大于b a>b>0
看系数正负,右边等于1时,哪个系数正,焦点就在对应坐标轴上 通过比较分母大小来判定焦点在哪一坐标轴上
c2=a2+b2 c2=a2-b2
对比差异 深化记忆
四、典题示范,学以致用
例1 已知双曲线两个焦点分别为F1(-5,0)F2(5,0),双曲线上一点P到F1,F2距离差的绝对值等于6,求双曲线的标准方程.
解:因为双曲线的焦点在x轴上,所以设它的标准
方程为
因为2a=6,2c=10,所以a=3,c=5,所以b2=52-32=16
因此,双曲线的标准方程为
X
待定系数法
口答1、判断下列双曲线的焦点在哪个轴上,并写出焦点坐标?
口答2、已知a=4,c=5,焦点在x轴上,求双曲线的方程;
3、已知两个焦点分别为F1(0,-2)F2(0,2),且经过点
,求双曲线的方程。
(±5,0)
(0,±5 )
当堂检测二
定义
图象
方程
焦点
a.b.c 的关系
确定焦点位置
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
F ( ±c, 0) F(0, ± c)
看系数正负,右边等于1时,哪个系数正,焦点就在对应坐标轴上
五、知识入网 本节聚焦
1、知识方面:
我学到了
2、能力方面:
我学会了
3、数学方法:
我感受到了
4、还有哪些疑问
1、作业:课本P61 A组 第2题
2、探究:类比椭圆的性质探究双曲线的性质
