3.2双曲线及其标准方程(2)(共22张PPT)
文档属性
| 名称 | 3.2双曲线及其标准方程(2)(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 11:44:30 | ||
图片预览







文档简介
(共22张PPT)
双曲线及其标准方程(2)
古希腊数学家阿波罗尼采用一个平面去截一个圆锥面,得到的截口曲线就称为圆锥曲线 ,通常提到的圆锥曲线包括椭圆,双曲线和抛物线.
椭圆
双曲线
抛物线
圆锥曲线名字的由来:
冷却塔
巴西利亚大教堂
花瓶
广州塔
F1
F2
y
x
o
y
o
x
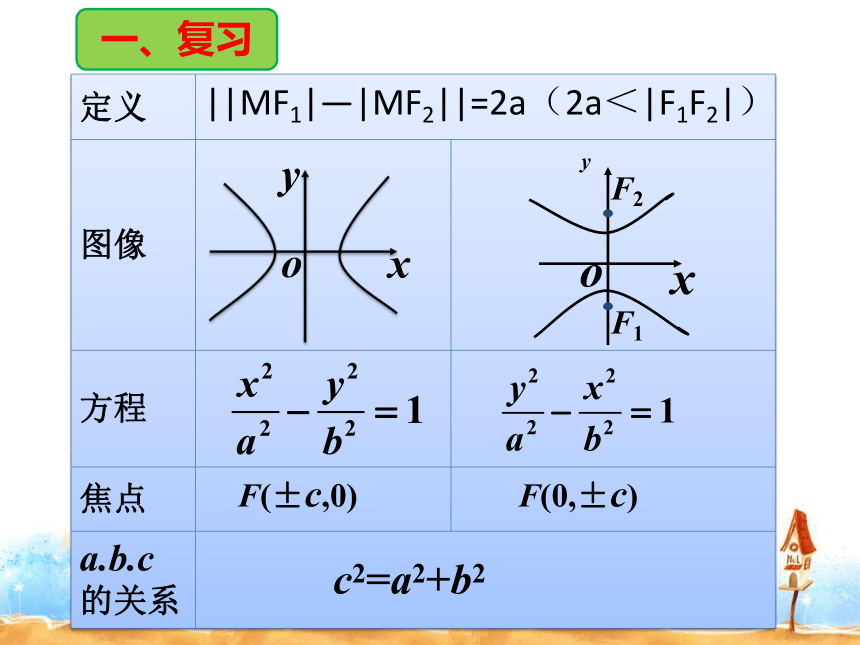
一、复习
椭圆与双曲线的比较:
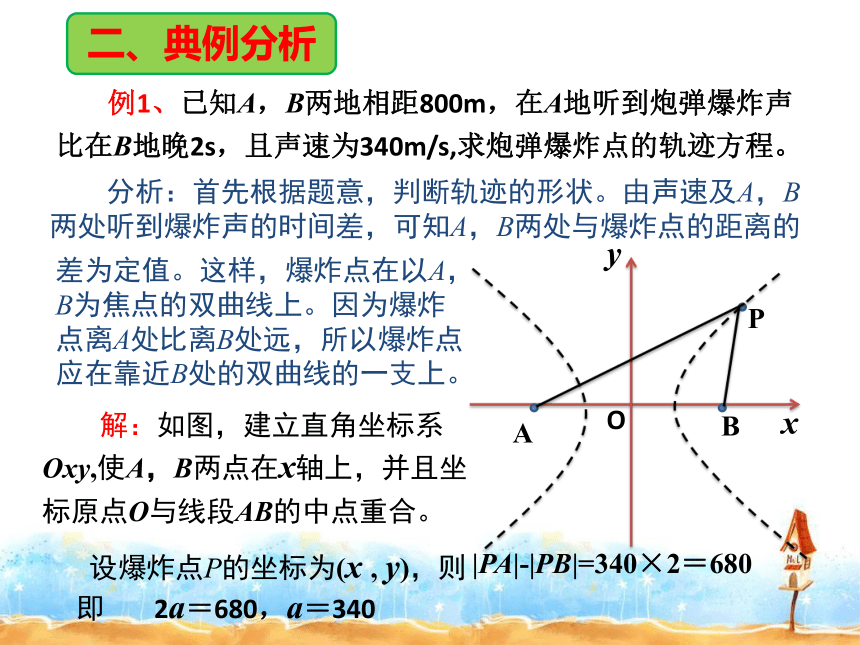
例1、已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程。
A
O
B
P
y
x
分析:首先根据题意,判断轨迹的形状。由声速及A,B两处听到爆炸声的时间差,可知A,B两处与爆炸点的距离的
解:如图,建立直角坐标系Oxy,使A,B两点在x轴上,并且坐标原点O与线段AB的中点重合。
设爆炸点P的坐标为(x , y),则
|PA|-|PB|=340×2=680
即 2a=680,a=340
二、典例分析
差为定值。这样,爆炸点在以A,B为焦点的双曲线上。因为爆炸点离A处比离B处远,所以爆炸点应在靠近B处的双曲线的一支上。
又 |AB|=800
所以 2c =800 c=400.
b2 = c2 –a2 =44400
因为|PA|-|PB|=340×2=680>0 , 所以x>0
因此炮弹爆炸点的轨迹(双曲线)的方程为:
利用两个不同的观测点A , B测得同一点P发出信号的时间差,可以确定点P所在双曲线的方程.如果再增设一个观测点C,利用B , C(或A , C)两处测得的点P 发出的信号的时间差,就可以求出另一个双曲线的方程.解这两个方程组成的方程组 ,就能确定点P的准确位置,这是双曲线的一个重要应用.
例2. 已知双曲线过P1 (-2 , )和P2 ( , 4)两点,求双曲线的标准方程.
解: 法一. (1)当双曲线的焦点在x轴上时,设双曲线方程
为:
因为 P1 ,P2 在双曲线上, 所以
(2)当双曲线的焦点在y轴上时,设双曲线方程为:
解之得
(不合题意,舍去)
因为 P1 ,P2 在双曲线上, 所以
解之得
即 a2 = 9 . b2 = 16.
故所求双曲线的方程为 :
法二. 因为双曲线的焦点位置不确定,所以设双曲线方程为:
因为 P1 ,P2 在双曲线上, 所以
解之得
故,所求双曲线的方程为 :
解法一采用了通法求解,因无法判断双曲线的焦点所在的位置,
分别设为:
两种情况,运用了分类讨论的思想,分别求解.解法二将双曲线的方程设为:
运算比较简便,但与椭圆设法不同,在解题时应注意方法技巧的灵活运用.
待定系数法
求椭圆与双曲线标准方程时,
可分别设为
如:焦点在y轴上,且过点
例3. 当 时 , 方程
表示的曲线怎么样变化
解 : (1) 当α =0o 时,方程为x2 =1 ,它表示两条平行直线
(2)当0 o< α <90o时,方程为
当0 o< α <45o时, .它表示焦点在y轴上的椭圆.
(3)当α =90o 时,方程为 y 2=1,它表示两条平行直线
(4)当90o < α < 180o 时.方程为
它表示焦点在y轴上的双曲线.
(5)当α =180o 时,方程为x2 =-1 ,它不表示任何曲线.
说明:解决这类题目的基本方法时分类讨论,在分类讨论的过程中应做到不重不漏,选择适当的分界点.
在讨论的过程中,方程表示的哪种曲线应说出该曲线的特征.
例4 , 设双曲线与椭圆 有共同的焦点,且与椭圆相交,一个交点的纵坐标为4,求双曲线的方程.
解法一. 由椭圆方程 得椭圆的焦点为
F 1(0 , -3) , F2(0 , 3) , A( ,4)是它与双曲线的一个交点.
设双曲线的方程为
解法二. 因为双曲线与椭圆 有相同的焦点,
故可设其方程为
将交点A( ,4)代入,得
例5、已知 B(-5,0),C(5,0)是三角形ABC的两个顶点,
求顶点A的轨迹方程。
解:在△ABC中,|BC|=10,
故顶点A的轨迹是以B、C为焦点的双曲线的左支,
又因 c=5,a=3,则 b=4
则顶点A的轨迹方程为
注意:若将 x<-3 写成 x<0 行吗?为什么?
1.已知椭圆 与双曲线
有相同的焦点F1、F2 , P为两条曲线的交点, 求|PF1| |PF2|的值.
F1
F2
P
解:由椭圆、双曲线的定义,得
上两式两边平方,得
上两式两边相减,得
三、巩固训练
小结
2、已知F1、F2为双曲线
的焦点,弦MN过F1且M、 N在同一支上,若 |MN|=7, 求△MF2N的周长.
M
N
F2
F1
x
o
y
解: ∵ 双曲线方程是
∴a2=16 , a=4 .
由双曲线的定义知,
上面两式相加,得
3、已知双曲线 16x2-9y2=144
①求焦点的坐标;
②设P为双曲线上一点,且|PF1| |PF2|=32,求:
③设P为双曲线上一点,且 F1PF2=120 ,求:
解: 双曲线方程化为
①、焦点的坐标为
P
F2
F1
x
o
y
② ∵ P为双曲线上一点,
③、
由余弦定理知
四、小结
本节巩固双曲线的定义及标准方程,主要研究了四种题型:
1、判断曲线类型;
2、求双曲线的标准方程:
①、定义法; ②、待定系数法。
3、双曲线的实际应用;
4、与双曲线的焦点三角形有关问题。
五、作业
1 、已知F1、F2为双曲线
的焦点,弦MN过F1且M、 N在同一支上,若 |MN|=7, 求△MF2N的周长.
2、已知双曲线 16x2-9y2=144
①求焦点的坐标;
②设P为双曲线上一点,且|PF1| |PF2|=32,求:
③设P为双曲线上一点,且 F1PF2=120 ,求:
多谢合作!
双曲线及其标准方程(2)
古希腊数学家阿波罗尼采用一个平面去截一个圆锥面,得到的截口曲线就称为圆锥曲线 ,通常提到的圆锥曲线包括椭圆,双曲线和抛物线.
椭圆
双曲线
抛物线
圆锥曲线名字的由来:
冷却塔
巴西利亚大教堂
花瓶
广州塔
F1
F2
y
x
o
y
o
x
一、复习
椭圆与双曲线的比较:
例1、已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程。
A
O
B
P
y
x
分析:首先根据题意,判断轨迹的形状。由声速及A,B两处听到爆炸声的时间差,可知A,B两处与爆炸点的距离的
解:如图,建立直角坐标系Oxy,使A,B两点在x轴上,并且坐标原点O与线段AB的中点重合。
设爆炸点P的坐标为(x , y),则
|PA|-|PB|=340×2=680
即 2a=680,a=340
二、典例分析
差为定值。这样,爆炸点在以A,B为焦点的双曲线上。因为爆炸点离A处比离B处远,所以爆炸点应在靠近B处的双曲线的一支上。
又 |AB|=800
所以 2c =800 c=400.
b2 = c2 –a2 =44400
因为|PA|-|PB|=340×2=680>0 , 所以x>0
因此炮弹爆炸点的轨迹(双曲线)的方程为:
利用两个不同的观测点A , B测得同一点P发出信号的时间差,可以确定点P所在双曲线的方程.如果再增设一个观测点C,利用B , C(或A , C)两处测得的点P 发出的信号的时间差,就可以求出另一个双曲线的方程.解这两个方程组成的方程组 ,就能确定点P的准确位置,这是双曲线的一个重要应用.
例2. 已知双曲线过P1 (-2 , )和P2 ( , 4)两点,求双曲线的标准方程.
解: 法一. (1)当双曲线的焦点在x轴上时,设双曲线方程
为:
因为 P1 ,P2 在双曲线上, 所以
(2)当双曲线的焦点在y轴上时,设双曲线方程为:
解之得
(不合题意,舍去)
因为 P1 ,P2 在双曲线上, 所以
解之得
即 a2 = 9 . b2 = 16.
故所求双曲线的方程为 :
法二. 因为双曲线的焦点位置不确定,所以设双曲线方程为:
因为 P1 ,P2 在双曲线上, 所以
解之得
故,所求双曲线的方程为 :
解法一采用了通法求解,因无法判断双曲线的焦点所在的位置,
分别设为:
两种情况,运用了分类讨论的思想,分别求解.解法二将双曲线的方程设为:
运算比较简便,但与椭圆设法不同,在解题时应注意方法技巧的灵活运用.
待定系数法
求椭圆与双曲线标准方程时,
可分别设为
如:焦点在y轴上,且过点
例3. 当 时 , 方程
表示的曲线怎么样变化
解 : (1) 当α =0o 时,方程为x2 =1 ,它表示两条平行直线
(2)当0 o< α <90o时,方程为
当0 o< α <45o时, .它表示焦点在y轴上的椭圆.
(3)当α =90o 时,方程为 y 2=1,它表示两条平行直线
(4)当90o < α < 180o 时.方程为
它表示焦点在y轴上的双曲线.
(5)当α =180o 时,方程为x2 =-1 ,它不表示任何曲线.
说明:解决这类题目的基本方法时分类讨论,在分类讨论的过程中应做到不重不漏,选择适当的分界点.
在讨论的过程中,方程表示的哪种曲线应说出该曲线的特征.
例4 , 设双曲线与椭圆 有共同的焦点,且与椭圆相交,一个交点的纵坐标为4,求双曲线的方程.
解法一. 由椭圆方程 得椭圆的焦点为
F 1(0 , -3) , F2(0 , 3) , A( ,4)是它与双曲线的一个交点.
设双曲线的方程为
解法二. 因为双曲线与椭圆 有相同的焦点,
故可设其方程为
将交点A( ,4)代入,得
例5、已知 B(-5,0),C(5,0)是三角形ABC的两个顶点,
求顶点A的轨迹方程。
解:在△ABC中,|BC|=10,
故顶点A的轨迹是以B、C为焦点的双曲线的左支,
又因 c=5,a=3,则 b=4
则顶点A的轨迹方程为
注意:若将 x<-3 写成 x<0 行吗?为什么?
1.已知椭圆 与双曲线
有相同的焦点F1、F2 , P为两条曲线的交点, 求|PF1| |PF2|的值.
F1
F2
P
解:由椭圆、双曲线的定义,得
上两式两边平方,得
上两式两边相减,得
三、巩固训练
小结
2、已知F1、F2为双曲线
的焦点,弦MN过F1且M、 N在同一支上,若 |MN|=7, 求△MF2N的周长.
M
N
F2
F1
x
o
y
解: ∵ 双曲线方程是
∴a2=16 , a=4 .
由双曲线的定义知,
上面两式相加,得
3、已知双曲线 16x2-9y2=144
①求焦点的坐标;
②设P为双曲线上一点,且|PF1| |PF2|=32,求:
③设P为双曲线上一点,且 F1PF2=120 ,求:
解: 双曲线方程化为
①、焦点的坐标为
P
F2
F1
x
o
y
② ∵ P为双曲线上一点,
③、
由余弦定理知
四、小结
本节巩固双曲线的定义及标准方程,主要研究了四种题型:
1、判断曲线类型;
2、求双曲线的标准方程:
①、定义法; ②、待定系数法。
3、双曲线的实际应用;
4、与双曲线的焦点三角形有关问题。
五、作业
1 、已知F1、F2为双曲线
的焦点,弦MN过F1且M、 N在同一支上,若 |MN|=7, 求△MF2N的周长.
2、已知双曲线 16x2-9y2=144
①求焦点的坐标;
②设P为双曲线上一点,且|PF1| |PF2|=32,求:
③设P为双曲线上一点,且 F1PF2=120 ,求:
多谢合作!
