3.3.2 抛物线的简单几何性质(第1课时)课件(共18张PPT)
文档属性
| 名称 | 3.3.2 抛物线的简单几何性质(第1课时)课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 363.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 11:52:12 | ||
图片预览




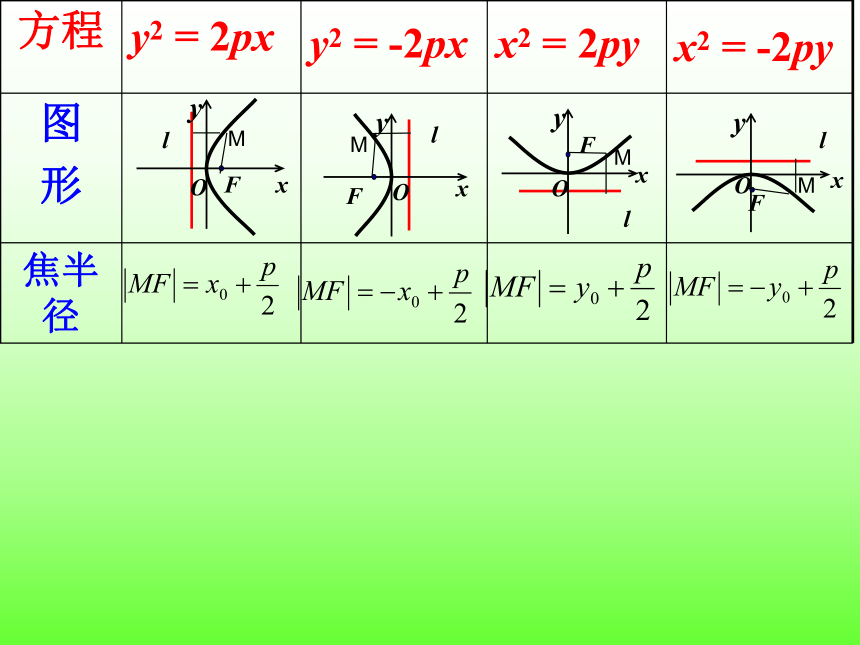


文档简介
(共18张PPT)
3.3.2
抛物线的简单几何性质
(第一课时)
高二数学选择性必修第一册 第三章 圆锥曲线的方程
平面内与一个定点F和一条定直线l(l不
经过点F)的距离相等的点的轨迹叫做抛物线
其中 定点F叫做抛物线的焦点
定直线 l 叫做抛物线的准线
一、知识回顾,温故知新
1.抛物线的定义
2.抛物线的图象与标准方程
l
H
F
M
·
·
图 象 方 程 焦 点 准 线
连接抛物线任意一点与焦点的线段
叫做抛物线的焦半径.
焦半径公式:
3.焦半径
(x0,y0)
H
d
y2 = 2px
方程
图 形
焦半径
y2 = 2px
y2 = -2px
x2 = 2py
x2 = -2py
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
M
M
M
M
由抛物线y2 =2px(p>0)
有
所以抛物线的范围为
如何研究抛物线y2 =2px(p>0)的几何性质
二、探究新知
1.范围
关于x轴
对称
即点(x,-y) 也在抛物线上,
故抛物线y2 = 2px(p>0)关于x轴对称.
则 (-y)2 = 2px
若点(x,y)在抛物线上, 即满足y2 = 2px,
2.对称性
定义:抛物线与它的对称轴的交点叫做抛物线的顶点.
y2 = 2px (p>0)中,
令x=0,则y=0.
即:抛物线y2 = 2px (p>0)的顶点(0,0).
3.顶点
抛物线上的点M与焦点F的距离和它到准线的距离之比,叫做抛物线的离心率.
由定义知, 抛物线y2 = 2px (p>0)的
离心率为e=1.
4.离心率
解:
设方程为:
又因为点M在抛物线上:
所以:
因此所求抛物线标准方程为:
三、巩固新知
例3.已知抛物线关于x轴对称,它的顶点在坐标
原点,并且经过点M(2, )求它的标准方程.
由题意
变式1
2).求顶点在坐标原点,对称轴为坐标轴,且
经过点 的抛物线的标准方程;
1).求顶点在坐标原点,对称轴为y轴,且经
过点 的抛物线的标准方程;
例4.斜率为1的直线 经过抛物线 的焦点,
且与抛物线相交于A、B两点,求线段AB的长.
例4.斜率为1的直线 经过抛物线 的焦点,
且与抛物线相交于A、B两点,求线段AB的长.
例4.斜率为1的直线 经过抛物线 的焦点,
且与抛物线相交于A、B两点,求线段AB的长.
解:F(1,0),∴直线 :y=x-1
变式2
2).已知抛物线 ,斜率为1的直线 经过的点P(0,1), 且与抛物线相交于A、B两点,求线段AB的长.
1).斜率为2的直线 经过抛物线 的焦点,
且与抛物线相交于A、B两点,求线段AB的长.
5
8
图 形 方程 焦点 准线 范围 顶点 对称轴 e
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2 = 2px
(p>0)
y2 = -2px
(p>0)
x2 = 2py
(p>0)
x2 = -2py
(p>0)
x≥0
y∈R
x≤0
y∈R
y≥0
x∈R
y ≤ 0
x∈R
(0,0)
x轴
y轴
1
四、课堂小结
方程
图 形
焦半径
y2 = 2px
y2 = -2px
x2 = 2py
x2 = -2py
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
M
M
M
M
1.已知抛物线的顶点在坐标原点,并且经过点
M(2,-4 )求它的标准方程.
2. 已知抛物线y2=8x,斜率为1的直线 经过
点P(2,0), 直线 与抛物线相交于A、B两点,
求线段AB的长.
五、课后作业
3.3.2
抛物线的简单几何性质
(第一课时)
高二数学选择性必修第一册 第三章 圆锥曲线的方程
平面内与一个定点F和一条定直线l(l不
经过点F)的距离相等的点的轨迹叫做抛物线
其中 定点F叫做抛物线的焦点
定直线 l 叫做抛物线的准线
一、知识回顾,温故知新
1.抛物线的定义
2.抛物线的图象与标准方程
l
H
F
M
·
·
图 象 方 程 焦 点 准 线
连接抛物线任意一点与焦点的线段
叫做抛物线的焦半径.
焦半径公式:
3.焦半径
(x0,y0)
H
d
y2 = 2px
方程
图 形
焦半径
y2 = 2px
y2 = -2px
x2 = 2py
x2 = -2py
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
M
M
M
M
由抛物线y2 =2px(p>0)
有
所以抛物线的范围为
如何研究抛物线y2 =2px(p>0)的几何性质
二、探究新知
1.范围
关于x轴
对称
即点(x,-y) 也在抛物线上,
故抛物线y2 = 2px(p>0)关于x轴对称.
则 (-y)2 = 2px
若点(x,y)在抛物线上, 即满足y2 = 2px,
2.对称性
定义:抛物线与它的对称轴的交点叫做抛物线的顶点.
y2 = 2px (p>0)中,
令x=0,则y=0.
即:抛物线y2 = 2px (p>0)的顶点(0,0).
3.顶点
抛物线上的点M与焦点F的距离和它到准线的距离之比,叫做抛物线的离心率.
由定义知, 抛物线y2 = 2px (p>0)的
离心率为e=1.
4.离心率
解:
设方程为:
又因为点M在抛物线上:
所以:
因此所求抛物线标准方程为:
三、巩固新知
例3.已知抛物线关于x轴对称,它的顶点在坐标
原点,并且经过点M(2, )求它的标准方程.
由题意
变式1
2).求顶点在坐标原点,对称轴为坐标轴,且
经过点 的抛物线的标准方程;
1).求顶点在坐标原点,对称轴为y轴,且经
过点 的抛物线的标准方程;
例4.斜率为1的直线 经过抛物线 的焦点,
且与抛物线相交于A、B两点,求线段AB的长.
例4.斜率为1的直线 经过抛物线 的焦点,
且与抛物线相交于A、B两点,求线段AB的长.
例4.斜率为1的直线 经过抛物线 的焦点,
且与抛物线相交于A、B两点,求线段AB的长.
解:F(1,0),∴直线 :y=x-1
变式2
2).已知抛物线 ,斜率为1的直线 经过的点P(0,1), 且与抛物线相交于A、B两点,求线段AB的长.
1).斜率为2的直线 经过抛物线 的焦点,
且与抛物线相交于A、B两点,求线段AB的长.
5
8
图 形 方程 焦点 准线 范围 顶点 对称轴 e
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
y2 = 2px
(p>0)
y2 = -2px
(p>0)
x2 = 2py
(p>0)
x2 = -2py
(p>0)
x≥0
y∈R
x≤0
y∈R
y≥0
x∈R
y ≤ 0
x∈R
(0,0)
x轴
y轴
1
四、课堂小结
方程
图 形
焦半径
y2 = 2px
y2 = -2px
x2 = 2py
x2 = -2py
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
l
F
y
x
O
M
M
M
M
1.已知抛物线的顶点在坐标原点,并且经过点
M(2,-4 )求它的标准方程.
2. 已知抛物线y2=8x,斜率为1的直线 经过
点P(2,0), 直线 与抛物线相交于A、B两点,
求线段AB的长.
五、课后作业
