3.3抛物线及其标准方程(共17张PPT)
文档属性
| 名称 | 3.3抛物线及其标准方程(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
抛物线及其标准方程
生活中存在着各种形式的抛物线
赵州桥:距今1400多年
北京2008奥林匹克体育馆
抛物线的生活实例
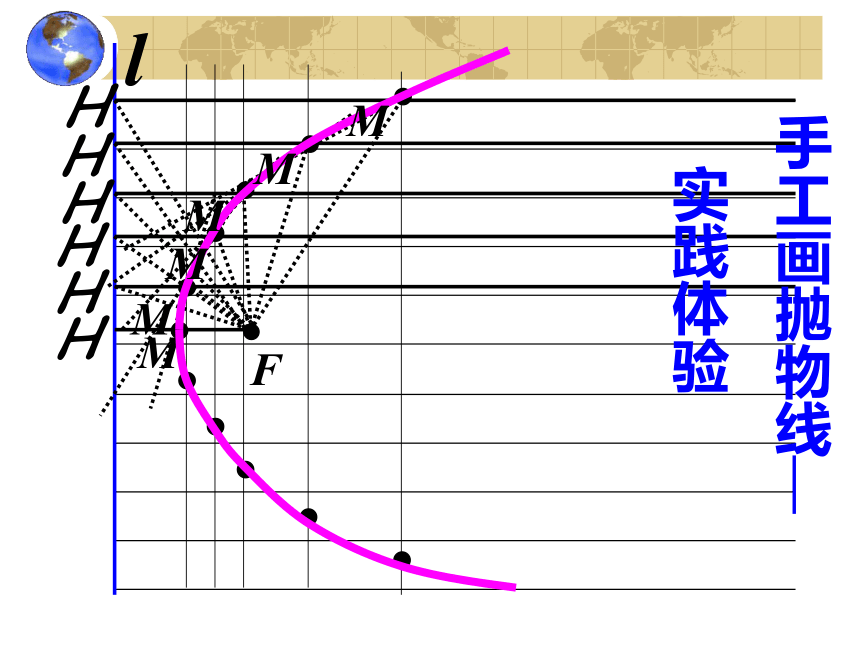
手工画抛物线—
实践体验
H
H
H
H
H
H
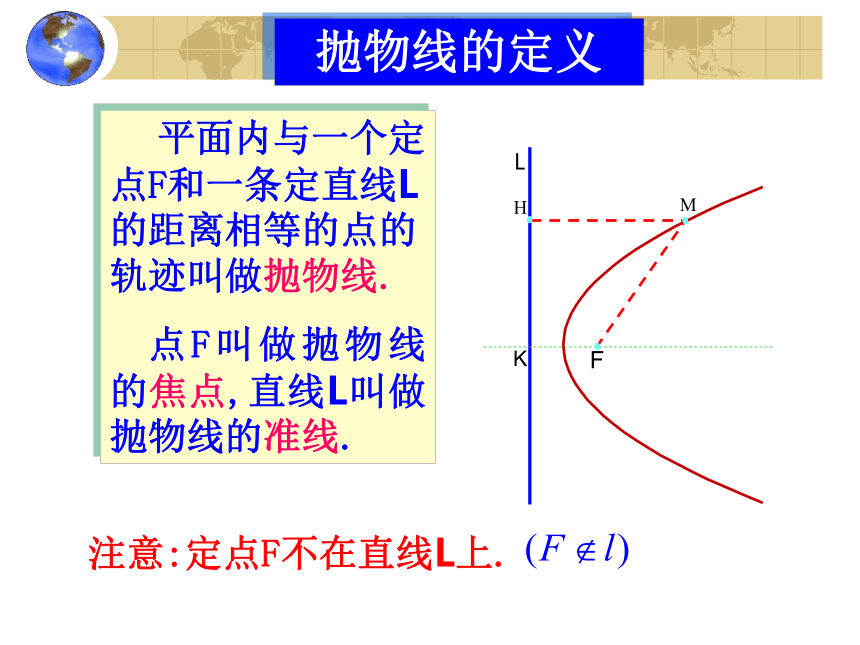
抛物线的定义
L
F
K
M
H
平面内与一个定点F和一条定直线L的距离相等的点的轨迹叫做抛物线.
点F叫做抛物线的焦点,直线L叫做抛物线的准线.
注意:定点F不在直线L上.
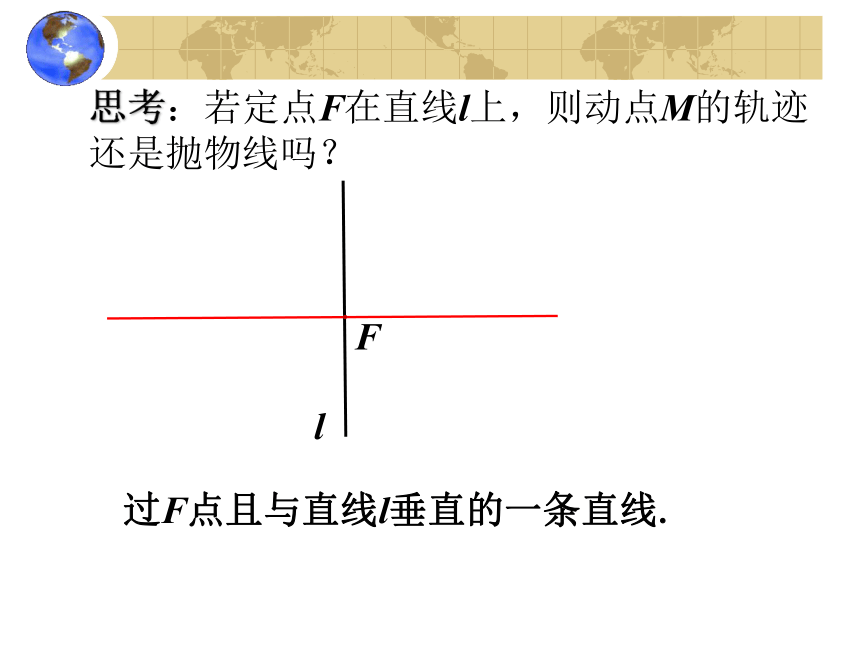
过F点且与直线l垂直的一条直线.
思考:若定点F在直线l上,则动点M的轨迹还是抛物线吗?
l
F
·
·
·
F
M
l
H
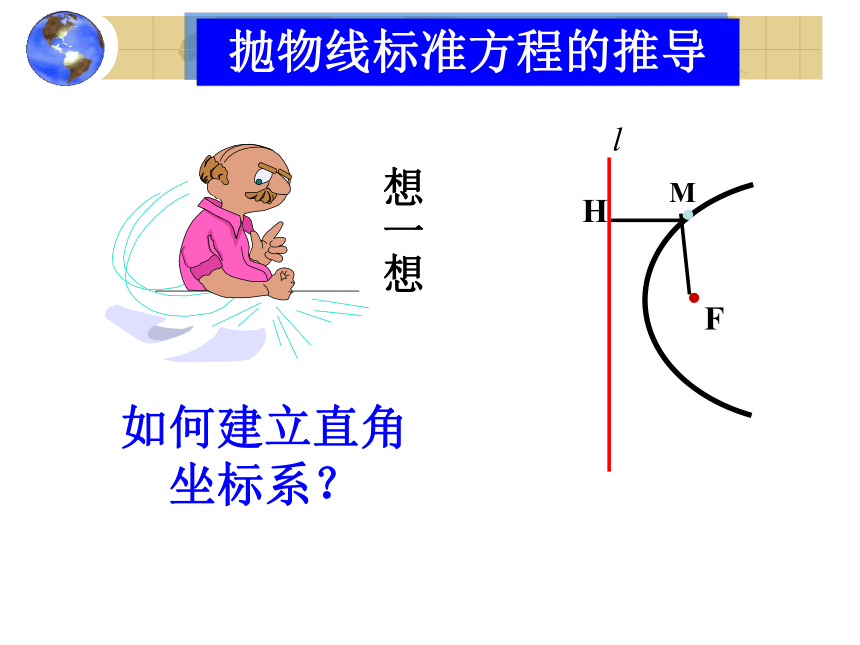
如何建立直角
坐标系?
想一想
抛物线标准方程的推导
L
F
K
M
H
(1)
L
F
K
M
H
L
F
K
M
H
(3)
(2)
设|KF|=p
化
限、代
设
建
解:以过F且垂直于直线 l 的直线为x轴,垂足为K.以FK的中点O为原点建立直角坐标系.
两边平方,整理得
x
K
y
O
F
M
l
·
·
·
(x,y)
H
d
由抛物线的定义知,抛物线就是点的集合
设M(x,y)是抛物线上任意一点,
点M到l的距离为d,
所以
直线l 的方程为
焦点
抛物线标准方程的推导
方程
叫做抛物线的标准方程.
焦点坐标是 ,它的准线方程是 。
其中p为正常数,它的几何意义是:
焦点到准线的距离。
抛物线的标准方程
L
F
K
M
H
抛物线的标准方程还有哪些形式
想一想?
其它形式的抛物线的焦点与准线呢?
抛物线的标准方程
物线的标准方程
如何确定抛物线焦点位置及开口方向
一次变量定焦点
开口方向看正负
图形
标准方程
焦点坐标
准线方程
x
H
F
O
M
l
y
x
y
H
F
O
M
l
x
y
H
F
O
M
l
x
y
H
F
O
M
l
例2: 求过点A(-3,2)的抛物线的标准方程。
.
A
O
y
x
思考题:M是抛物线y2 = 2px(P>0)上一点,若点
M 的横坐标为X0,则点M到焦点的距离是:
X0 + —
2
p
O
y
x
F
M
.
4.注重数形结合的思想;
注重分类讨论的思想.
1.抛物线的定义;
2.抛物线的标准方程有四种不同的形式,
每一对焦点和准线对应一种形式;
3.p的几何意义是:
焦点到准线的距离;
课堂小结
课后作业
1.课后练习:课本P67页 1,2,3题;
2.课后思考: 习题2.4A组 2,3题.
谢谢指导
抛物线及其标准方程
生活中存在着各种形式的抛物线
赵州桥:距今1400多年
北京2008奥林匹克体育馆
抛物线的生活实例
手工画抛物线—
实践体验
H
H
H
H
H
H
抛物线的定义
L
F
K
M
H
平面内与一个定点F和一条定直线L的距离相等的点的轨迹叫做抛物线.
点F叫做抛物线的焦点,直线L叫做抛物线的准线.
注意:定点F不在直线L上.
过F点且与直线l垂直的一条直线.
思考:若定点F在直线l上,则动点M的轨迹还是抛物线吗?
l
F
·
·
·
F
M
l
H
如何建立直角
坐标系?
想一想
抛物线标准方程的推导
L
F
K
M
H
(1)
L
F
K
M
H
L
F
K
M
H
(3)
(2)
设|KF|=p
化
限、代
设
建
解:以过F且垂直于直线 l 的直线为x轴,垂足为K.以FK的中点O为原点建立直角坐标系.
两边平方,整理得
x
K
y
O
F
M
l
·
·
·
(x,y)
H
d
由抛物线的定义知,抛物线就是点的集合
设M(x,y)是抛物线上任意一点,
点M到l的距离为d,
所以
直线l 的方程为
焦点
抛物线标准方程的推导
方程
叫做抛物线的标准方程.
焦点坐标是 ,它的准线方程是 。
其中p为正常数,它的几何意义是:
焦点到准线的距离。
抛物线的标准方程
L
F
K
M
H
抛物线的标准方程还有哪些形式
想一想?
其它形式的抛物线的焦点与准线呢?
抛物线的标准方程
物线的标准方程
如何确定抛物线焦点位置及开口方向
一次变量定焦点
开口方向看正负
图形
标准方程
焦点坐标
准线方程
x
H
F
O
M
l
y
x
y
H
F
O
M
l
x
y
H
F
O
M
l
x
y
H
F
O
M
l
例2: 求过点A(-3,2)的抛物线的标准方程。
.
A
O
y
x
思考题:M是抛物线y2 = 2px(P>0)上一点,若点
M 的横坐标为X0,则点M到焦点的距离是:
X0 + —
2
p
O
y
x
F
M
.
4.注重数形结合的思想;
注重分类讨论的思想.
1.抛物线的定义;
2.抛物线的标准方程有四种不同的形式,
每一对焦点和准线对应一种形式;
3.p的几何意义是:
焦点到准线的距离;
课堂小结
课后作业
1.课后练习:课本P67页 1,2,3题;
2.课后思考: 习题2.4A组 2,3题.
谢谢指导
