3.2双曲线的简单几何性质 (2)(共24张PPT)
文档属性
| 名称 | 3.2双曲线的简单几何性质 (2)(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 947.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 11:52:54 | ||
图片预览






文档简介
(共24张PPT)
双曲线的简单几何性质(2)
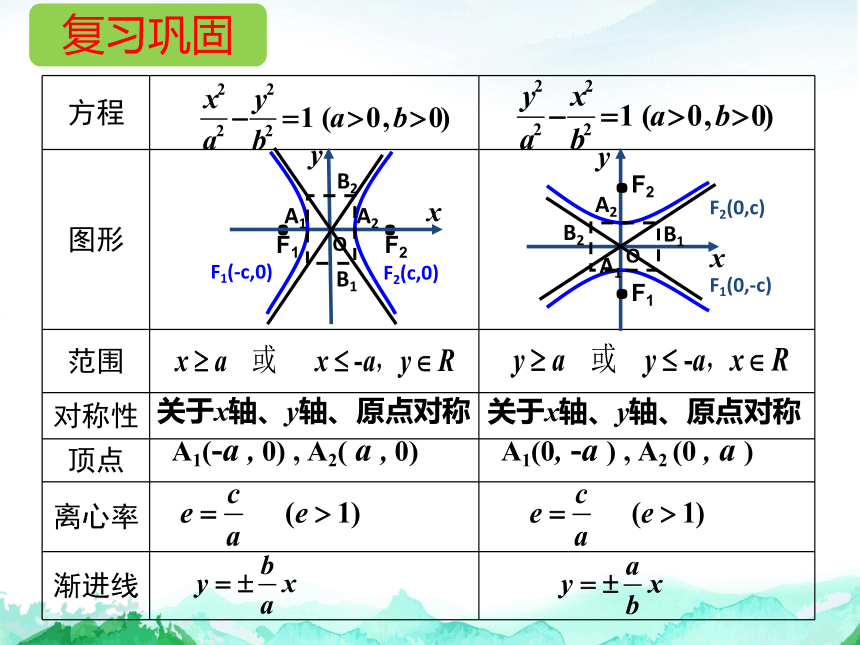
方程
图形
范围
对称性
顶点
离心率
渐进线
.
.
y
B2
A1
A2
B1
x
O
F2
F1
F1(-c,0)
F2(c,0)
x
B1
y
O
.
F2
F1
B2
A1
A2
.
F2(0,c)
F1(0,-c)
关于x轴、y轴、原点对称
关于x轴、y轴、原点对称
A1(-a , 0) , A2( a , 0)
A1(0, -a ) , A2 (0 , a )
复习巩固
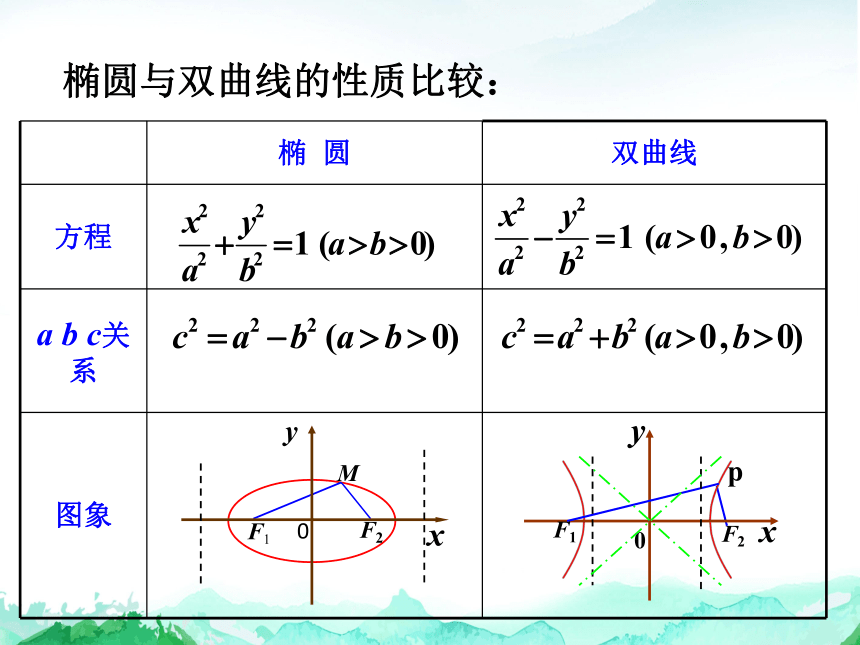
椭 圆 双曲线
方程
a b c关系
图象
y
x
F1
0
F2
M
x
y
0
F1
F2
p
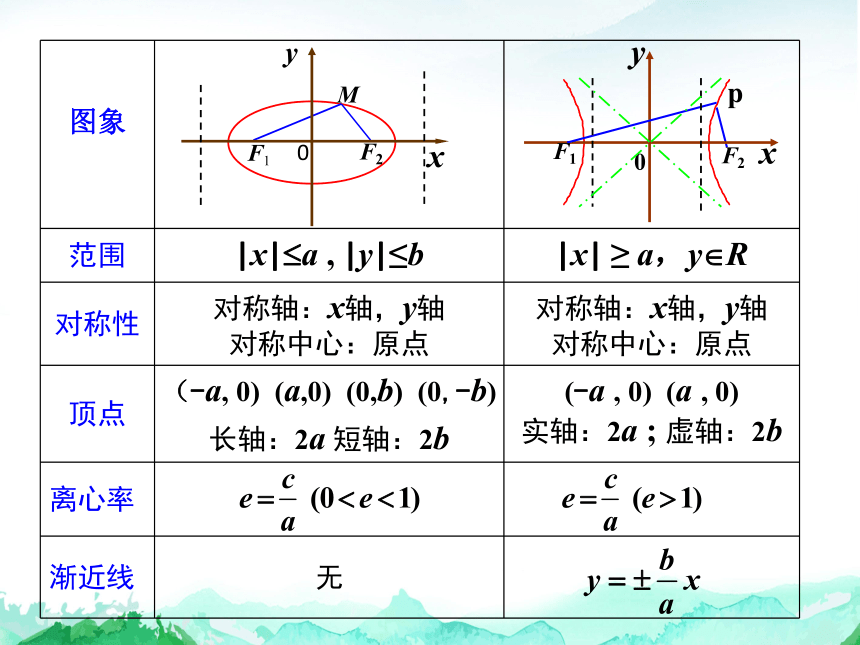
椭圆与双曲线的性质比较:
图象
范围 |x| a , |y|≤b |x| ≥ a,y R
对称性 对称轴:x轴,y轴 对称中心:原点 对称轴:x轴,y轴
对称中心:原点
顶点 (-a, 0) (a,0) (0,b) (0,-b) 长轴:2a 短轴:2b (-a , 0) (a , 0)
实轴:2a ; 虚轴:2b
离心率
渐近线 无
y
x
F1
0
F2
M
x
y
0
F1
F2
p
例1.求下列双曲线的渐近线方程,并画出图像:
0
x
y
如何记忆双曲线的渐进线方程?
解:
典例分析
能不能直接由双曲线方程推出渐近线方程?
结论:
双曲线方程
中,把1改为0,得
说明:
的渐进线相同,都是直线
和
即
归纳
(1)
(2)
例2.已知双曲线的渐近线是 ,并且双曲线过点
求双曲线方程。
说明:设双曲线方程为
若求得λ>0,则双曲线的焦点在x轴上;
若求得λ<0,则双曲线的焦点在y轴上。
例3.求下列双曲线的标准方程:
例题讲解
法二:设双曲线方程为
∴ 双曲线方程为
∴ ,
解之得k=4,
1、“共渐近线”的双曲线的应用
λ>0表示焦点在x轴上的双曲线;
λ<0表示焦点在y轴上的双曲线。
我们知道,电能是现代生活不可缺少的能源,目前我国主要靠火力发电,而火力发电主要是在火力发电厂中进行,火力发电厂简称“火电厂”,其形状就像照片中“粗烟囱”.那么这些“粗烟囱”是怎样建成的呢?
冷却通风塔
例题讲解
例2、双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面,它的最小半径为12m,上口半径为13m,下口半径为25m,高55m.试选择适当的坐标系,求出此双曲线的方程(精确到1m).
A′
A
0
x
C′
C
B′
B
y
13
12
25
解:如图,
在冷却塔的轴截面所在的平面上建立直角坐标系xoy,使小圆的直径AA′
在x轴上,圆心与原点重合。这时,
A′
A
0
x
C′
C
B′
B
y
13
12
25
令点C的坐标为(13,y),则点B的坐标为(25,y-55)。
因为点B、 C在双曲线上,所以
设双曲线的方程为
②
①
由方程② ,得
(负值舍去),
代入方程①,得
用计数器解方程③ ,得
化简得
③
所以,所求双曲线的方程为
小结
【总结提升】
已知双曲线的几何性质,求其标准方程的方法步骤:
(1)确定焦点所在的位置,以确定双曲线方程的形式;
(2)确立关于a,b,c的方程(组),求出参数a,b,c;
(3)写出标准方程.
定位
定量
H
F
d
y
x
o
M
l
双曲线的第二定义:
y
.
.
F2
F1
O
M
.
x
对双曲线
右焦点F2(c,0),对应的右准线方程是
左焦点F1(-c,0),对应的左准线方程是
对双曲线
上焦点F2(0, c),对应的上准线方程是
下焦点F1(0,-c),对应的下准线方程是
动画
叙述为:若M ( x , y )与定点 F (c , 0) 的距离和它到定直
线 l: 的距离的比是常数 ,则
点 M 的轨迹是一个双曲线,其方程为
例4、
证明:
P
说明:|PF1|, |PF2|称为双曲线的焦半径.
y
.
.
F2
F1
O
.
x
双曲线中应注意的几个问题:
(1)双曲线是两支曲线,而椭圆是一条封闭的曲线;
(2)双曲线的两条渐近线是区别于其他圆锥曲线所特有的;
(3)双曲线只有两个顶点,离心率e>1;
(4)注意双曲线中a,b,c,e的等量关系与椭圆中a,b,c,e的不同.
课堂总结
回顾直线与椭圆的位置关系及判断方法,思考直线与双曲线有何位置关系,如何判断?
知识要点:
技法要点:
2、双曲线的第二定义:
双曲线的准线方程是
3、双曲线的焦半径。对方程
小结
的渐进线是
的渐进线是
双曲线的简单几何性质(2)
方程
图形
范围
对称性
顶点
离心率
渐进线
.
.
y
B2
A1
A2
B1
x
O
F2
F1
F1(-c,0)
F2(c,0)
x
B1
y
O
.
F2
F1
B2
A1
A2
.
F2(0,c)
F1(0,-c)
关于x轴、y轴、原点对称
关于x轴、y轴、原点对称
A1(-a , 0) , A2( a , 0)
A1(0, -a ) , A2 (0 , a )
复习巩固
椭 圆 双曲线
方程
a b c关系
图象
y
x
F1
0
F2
M
x
y
0
F1
F2
p
椭圆与双曲线的性质比较:
图象
范围 |x| a , |y|≤b |x| ≥ a,y R
对称性 对称轴:x轴,y轴 对称中心:原点 对称轴:x轴,y轴
对称中心:原点
顶点 (-a, 0) (a,0) (0,b) (0,-b) 长轴:2a 短轴:2b (-a , 0) (a , 0)
实轴:2a ; 虚轴:2b
离心率
渐近线 无
y
x
F1
0
F2
M
x
y
0
F1
F2
p
例1.求下列双曲线的渐近线方程,并画出图像:
0
x
y
如何记忆双曲线的渐进线方程?
解:
典例分析
能不能直接由双曲线方程推出渐近线方程?
结论:
双曲线方程
中,把1改为0,得
说明:
的渐进线相同,都是直线
和
即
归纳
(1)
(2)
例2.已知双曲线的渐近线是 ,并且双曲线过点
求双曲线方程。
说明:设双曲线方程为
若求得λ>0,则双曲线的焦点在x轴上;
若求得λ<0,则双曲线的焦点在y轴上。
例3.求下列双曲线的标准方程:
例题讲解
法二:设双曲线方程为
∴ 双曲线方程为
∴ ,
解之得k=4,
1、“共渐近线”的双曲线的应用
λ>0表示焦点在x轴上的双曲线;
λ<0表示焦点在y轴上的双曲线。
我们知道,电能是现代生活不可缺少的能源,目前我国主要靠火力发电,而火力发电主要是在火力发电厂中进行,火力发电厂简称“火电厂”,其形状就像照片中“粗烟囱”.那么这些“粗烟囱”是怎样建成的呢?
冷却通风塔
例题讲解
例2、双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面,它的最小半径为12m,上口半径为13m,下口半径为25m,高55m.试选择适当的坐标系,求出此双曲线的方程(精确到1m).
A′
A
0
x
C′
C
B′
B
y
13
12
25
解:如图,
在冷却塔的轴截面所在的平面上建立直角坐标系xoy,使小圆的直径AA′
在x轴上,圆心与原点重合。这时,
A′
A
0
x
C′
C
B′
B
y
13
12
25
令点C的坐标为(13,y),则点B的坐标为(25,y-55)。
因为点B、 C在双曲线上,所以
设双曲线的方程为
②
①
由方程② ,得
(负值舍去),
代入方程①,得
用计数器解方程③ ,得
化简得
③
所以,所求双曲线的方程为
小结
【总结提升】
已知双曲线的几何性质,求其标准方程的方法步骤:
(1)确定焦点所在的位置,以确定双曲线方程的形式;
(2)确立关于a,b,c的方程(组),求出参数a,b,c;
(3)写出标准方程.
定位
定量
H
F
d
y
x
o
M
l
双曲线的第二定义:
y
.
.
F2
F1
O
M
.
x
对双曲线
右焦点F2(c,0),对应的右准线方程是
左焦点F1(-c,0),对应的左准线方程是
对双曲线
上焦点F2(0, c),对应的上准线方程是
下焦点F1(0,-c),对应的下准线方程是
动画
叙述为:若M ( x , y )与定点 F (c , 0) 的距离和它到定直
线 l: 的距离的比是常数 ,则
点 M 的轨迹是一个双曲线,其方程为
例4、
证明:
P
说明:|PF1|, |PF2|称为双曲线的焦半径.
y
.
.
F2
F1
O
.
x
双曲线中应注意的几个问题:
(1)双曲线是两支曲线,而椭圆是一条封闭的曲线;
(2)双曲线的两条渐近线是区别于其他圆锥曲线所特有的;
(3)双曲线只有两个顶点,离心率e>1;
(4)注意双曲线中a,b,c,e的等量关系与椭圆中a,b,c,e的不同.
课堂总结
回顾直线与椭圆的位置关系及判断方法,思考直线与双曲线有何位置关系,如何判断?
知识要点:
技法要点:
2、双曲线的第二定义:
双曲线的准线方程是
3、双曲线的焦半径。对方程
小结
的渐进线是
的渐进线是
