解直角三角形单元测试
图片预览

文档简介
解直角三角形 单元测试
一、填空题
1.若直角三角形两条直角边长分别为5和12,则斜边上的中线长为________.
2.若等腰直角三角形的一边长是2,则它的面积为___________.
3.△ABC中,∠C=90°,a=6,b=8,则sinA=_____________.
4.在△ABC中,∠C=90°,,则cosB=___________.
5.若,则锐角a=__________度.
6.Rt△ABC中,∠C=90°,,则∠B=_________度.
7.△ABC中,∠C=90°,,则AC=_________.
8.在离大楼15m的地面上看大楼顶部仰角为65°,则大楼高约__________m(精确到lm).
9.在电线杆离地面8m的地方向地面拉一条缆绳以固定电线杆,如果缆绳与地面成
60°角,那么需要缆绳__________m(忽略打结部分).
10.一个斜坡的坡度是1:3,高度是4m,则他从坡底到坡顶部所走的路程大约是___________m(精确到0.1m).
11.=
12.在△ABC中,∠A=30o,tan B= ,BC=,则AB的长为 .
13.锐角A满足2 sin(A-15)=,则∠A= .
14.已知tan B=,则sin= .
15.某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为米,则这个破面的坡度为 .
16.如图所示,小明在家里楼顶上的点A处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A处看电梯楼顶部点B处的仰角为60°,在点A处看这栋电梯楼底部点C处的俯角为45°,两栋楼之间的距离为30m,则电梯楼的高BC为______米(保留根号).
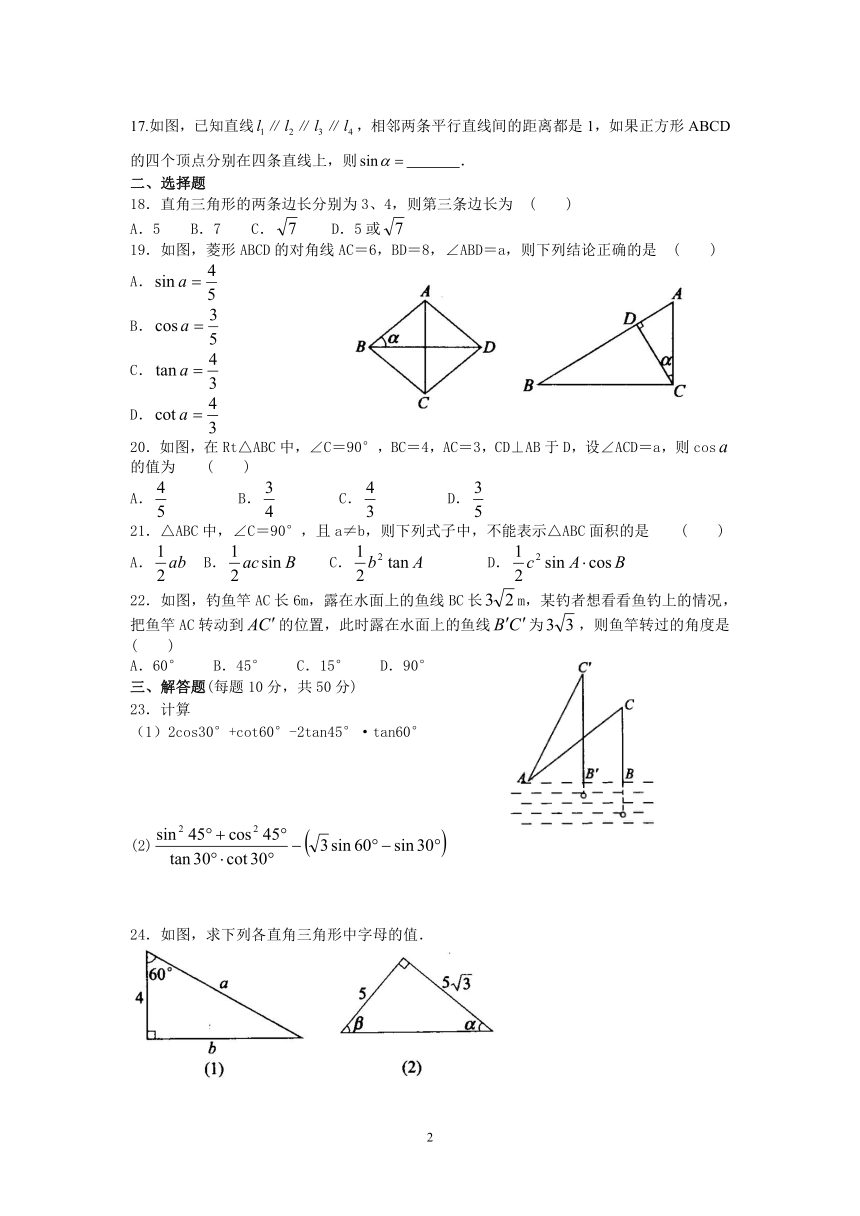
17.如图,已知直线∥∥∥,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则 .
二、选择题
18.直角三角形的两条边长分别为3、4,则第三条边长为 ( )
A.5 B.7 C. D.5或
19.如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=a,则下列结论正确的是 ( )
A.
B.
C.
D.
20.如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,CD⊥AB于D,设∠ACD=a,则cos的值为 ( )
A. B. C. D.
21.△ABC中,∠C=90°,且a≠b,则下列式子中,不能表示△ABC面积的是 ( )
A. B. C. D.
22.如图,钓鱼竿AC长6m,露在水面上的鱼线BC长m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到的位置,此时露在水面上的鱼线为,则鱼竿转过的角度是 ( )
A.60° B.45° C.15° D.90°
三、解答题(每题10分,共50分)
23.计算
(1)2cos30°+cot60°-2tan45°·tan60°
(2)
24.如图,求下列各直角三角形中字母的值.
25.如图是直线y=-2x+5的图象,求锐角a的四个三角函数值,并求角a。
26.如图,梯形ABCD中,AB⊥BC,∠BAC=60°,∠ADC=135°,,求梯形的面积和周长.
27.某兴趣小组用高为1.2米的仪器测量建筑物CD的高度.如示意图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为.测得A,B之间的距离为4米,,,试求建筑物CD的高度.
28.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°, ∠E=45°,∠A=60°,AC=10,试求CD的长.
29.(2012山西)如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A.B的距离,飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,求岛屿两端A.B的距离(结果精确到0.1米,参考数据:)
30.如图,台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力,据气象观测,距沿海某城市A的正南方向220km的B处有一台风中心,其中心最大风力为12级,每远离台风中心20km,风力就会减弱一级,该台风中心现正以15km/h的速度沿北偏东30°方向往C处移动,且台风中心风力不变.若城市所受风力达到或超过四级,则称为受台风影响.
(1)该城市是否会受到这次台风的影响?请说明理由.
(2)若会受台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
一、填空题
1.若直角三角形两条直角边长分别为5和12,则斜边上的中线长为________.
2.若等腰直角三角形的一边长是2,则它的面积为___________.
3.△ABC中,∠C=90°,a=6,b=8,则sinA=_____________.
4.在△ABC中,∠C=90°,,则cosB=___________.
5.若,则锐角a=__________度.
6.Rt△ABC中,∠C=90°,,则∠B=_________度.
7.△ABC中,∠C=90°,,则AC=_________.
8.在离大楼15m的地面上看大楼顶部仰角为65°,则大楼高约__________m(精确到lm).
9.在电线杆离地面8m的地方向地面拉一条缆绳以固定电线杆,如果缆绳与地面成
60°角,那么需要缆绳__________m(忽略打结部分).
10.一个斜坡的坡度是1:3,高度是4m,则他从坡底到坡顶部所走的路程大约是___________m(精确到0.1m).
11.=
12.在△ABC中,∠A=30o,tan B= ,BC=,则AB的长为 .
13.锐角A满足2 sin(A-15)=,则∠A= .
14.已知tan B=,则sin= .
15.某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为米,则这个破面的坡度为 .
16.如图所示,小明在家里楼顶上的点A处,测量建在与小明家楼房同一水平线上相邻的电梯楼的高,在点A处看电梯楼顶部点B处的仰角为60°,在点A处看这栋电梯楼底部点C处的俯角为45°,两栋楼之间的距离为30m,则电梯楼的高BC为______米(保留根号).
17.如图,已知直线∥∥∥,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则 .
二、选择题
18.直角三角形的两条边长分别为3、4,则第三条边长为 ( )
A.5 B.7 C. D.5或
19.如图,菱形ABCD的对角线AC=6,BD=8,∠ABD=a,则下列结论正确的是 ( )
A.
B.
C.
D.
20.如图,在Rt△ABC中,∠C=90°,BC=4,AC=3,CD⊥AB于D,设∠ACD=a,则cos的值为 ( )
A. B. C. D.
21.△ABC中,∠C=90°,且a≠b,则下列式子中,不能表示△ABC面积的是 ( )
A. B. C. D.
22.如图,钓鱼竿AC长6m,露在水面上的鱼线BC长m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到的位置,此时露在水面上的鱼线为,则鱼竿转过的角度是 ( )
A.60° B.45° C.15° D.90°
三、解答题(每题10分,共50分)
23.计算
(1)2cos30°+cot60°-2tan45°·tan60°
(2)
24.如图,求下列各直角三角形中字母的值.
25.如图是直线y=-2x+5的图象,求锐角a的四个三角函数值,并求角a。
26.如图,梯形ABCD中,AB⊥BC,∠BAC=60°,∠ADC=135°,,求梯形的面积和周长.
27.某兴趣小组用高为1.2米的仪器测量建筑物CD的高度.如示意图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为.测得A,B之间的距离为4米,,,试求建筑物CD的高度.
28.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°, ∠E=45°,∠A=60°,AC=10,试求CD的长.
29.(2012山西)如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A.B的距离,飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,求岛屿两端A.B的距离(结果精确到0.1米,参考数据:)
30.如图,台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力,据气象观测,距沿海某城市A的正南方向220km的B处有一台风中心,其中心最大风力为12级,每远离台风中心20km,风力就会减弱一级,该台风中心现正以15km/h的速度沿北偏东30°方向往C处移动,且台风中心风力不变.若城市所受风力达到或超过四级,则称为受台风影响.
(1)该城市是否会受到这次台风的影响?请说明理由.
(2)若会受台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
