沪科版数学八年级下册19.3.2 第2课时 菱形的判定同步课件(共21张PPT)
文档属性
| 名称 | 沪科版数学八年级下册19.3.2 第2课时 菱形的判定同步课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 478.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 21:23:42 | ||
图片预览



文档简介
(共21张PPT)
第19章 四边形
19.3.2 第2课时 菱形的判定
知识回顾
菱形的定义是什么?性质有哪些?
一组邻边相等
有一组邻边相等的平行四边形叫做菱形
平行四边形
菱形
菱形的性质
菱形的四条边都相等
菱形的两组对边分别平行
菱形的两条对角线互相平分
边
对角线
角
菱形的两组对角分别相等
菱形的邻角分别互补
菱形的两条对角线互相垂直
菱形的每一条对角线平分一组对角
菱形
获取新知
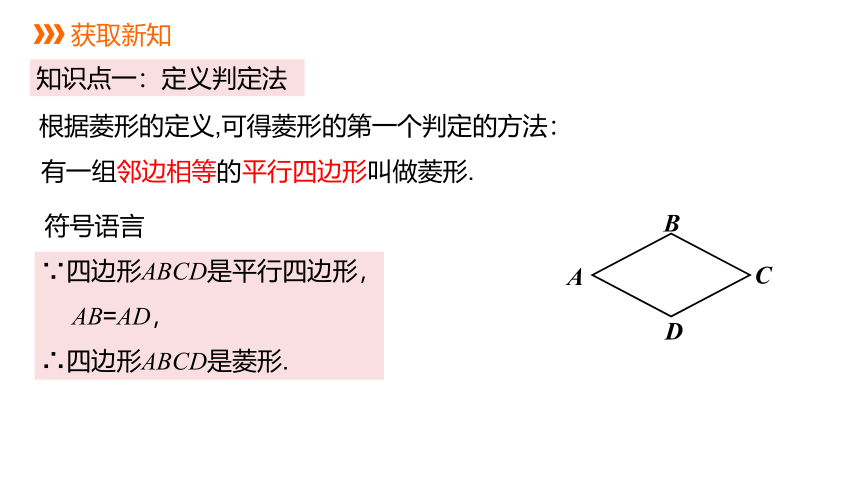
知识点一:定义判定法
根据菱形的定义,可得菱形的第一个判定的方法:
∵四边形ABCD是平行四边形,
AB=AD,
∴四边形ABCD是菱形.
符号语言
有一组邻边相等的平行四边形叫做菱形.
A
B
C
D
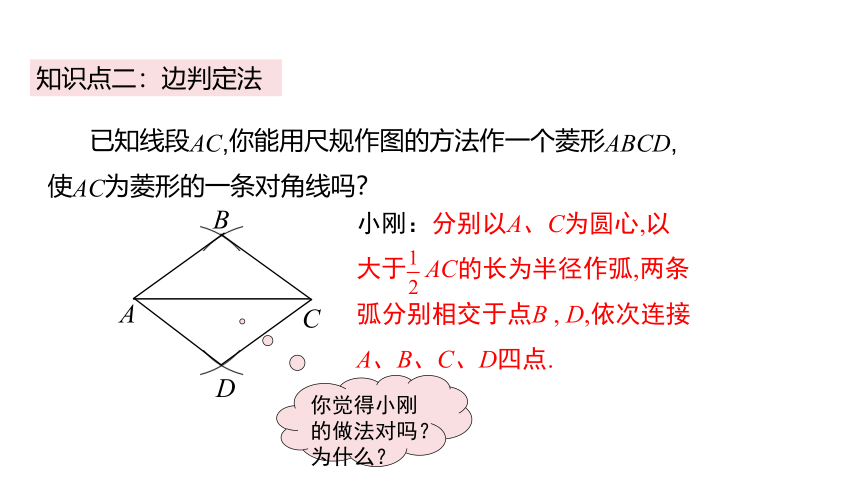
知识点二:边判定法
已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗?
C
A
B
D
小刚:分别以A、C为圆心,以大于 AC的长为半径作弧,两条 弧分别相交于点B , D,依次连接A、B、C、D四点.
你觉得小刚的做法对吗?为什么?
判定定理1:四边都相等的四边形是菱形
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
A
B
C
D
证明:∵AB=BC=CD=AD;
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
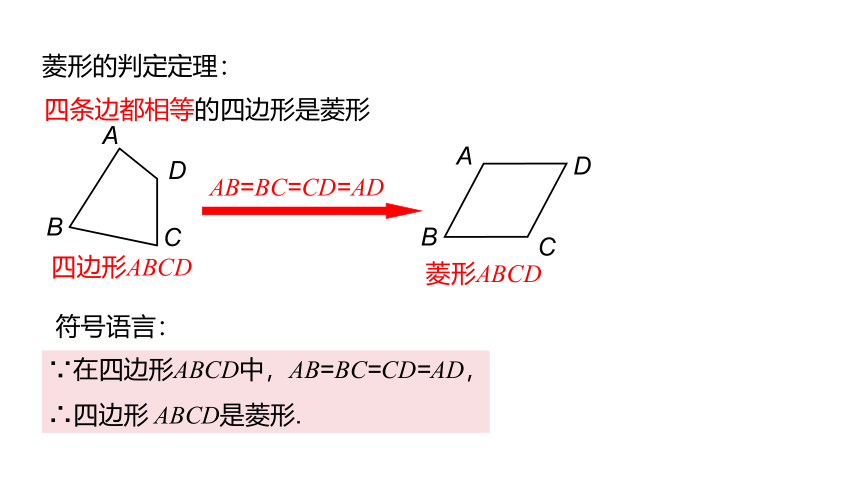
四条边都相等的四边形是菱形
AB=BC=CD=AD
∵在四边形ABCD中,AB=BC=CD=AD,
∴四边形 ABCD是菱形.
A
B
C
D
菱形ABCD
菱形的判定定理:
四边形ABCD
A
B
C
D
符号语言:
例题讲解
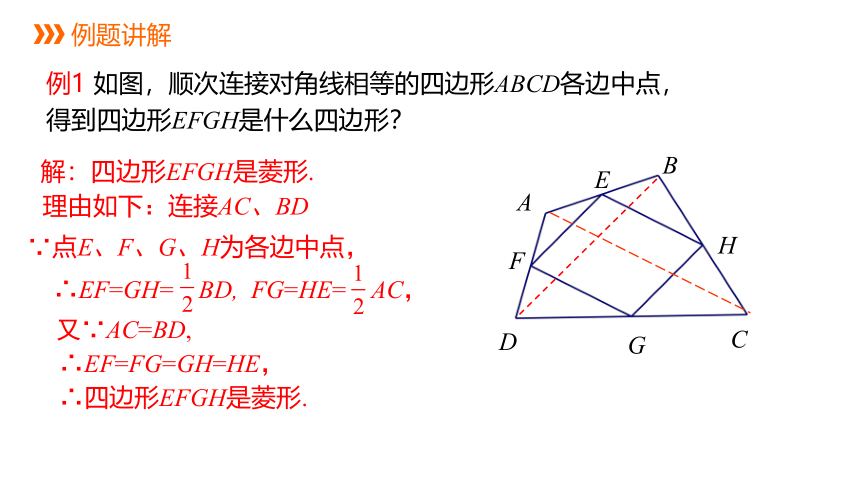
例1 如图,顺次连接对角线相等的四边形ABCD各边中点,得到四边形EFGH是什么四边形?
解:四边形EFGH是菱形.
又∵AC=BD,
∵点E、F、G、H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
理由如下:连接AC、BD
∴EF=GH= BD, FG=HE= AC,
C
A
B
D
E
F
G
H
知识点二:对角线判定法
前面我们用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形.那么转动木条,这个平行四边形什么时候变成菱形 对此你有什么猜想?
获取新知
判定定理2:对角线互相垂直的平行四边形是菱形.
已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O ,AC⊥BD.
求证:□ABCD是菱形.
A
B
C
O
D
证明: ∵四边形ABCD是平行四边形.
∴OA=OC.
又∵AC⊥BD,
∴BD是线段AC的垂直平分线.
∴BA=BC.
∴四边形ABCD是菱形(菱形的定义).
对角线互相垂直的平行四边形是菱形.
AC⊥BD
∵在□ABCD中,AC⊥BD,
∴ □ABCD是菱形.
符号语言:
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
菱形的判定定理:
例题讲解
例2 如图,在 ABCD中,AC=8,BD=6,AB=5,
求AD的长.
A
B
C
D
O
解:∵四边形ABCD是平行四边形,
∴OA= AC=4,OB= BD=3.
又∵AB=5,满足AB2=OA2+OB2,
∴△AOB为直角三角形,及OA⊥OB.
∴ ABCD是菱形,AD=AB=5.
归纳对比
随堂演练
1. 如图,要使 ABCD成为菱形,则需添加的一个条件可以是( )
A. AC=AD B. BA=BC
C. ∠ABC=90° D. AC=BD
B
2. 下列命题中,正确的是( )
A.对角线相等的四边形是菱形
B.对角线互相垂直的四边形是菱形
C.对角线相等的平行四边形是菱形
D.对角线互相垂直的平行四边形是菱形
D
3. 如图,已知△ABC,AB=AC,将△ABC沿边BC翻折,得到的△DBC与原△ABC拼成四边形ABDC,则能直接判定四边形ABDC是菱形的依据是( )
A.一组邻边相等的平行四边形是菱形
B.四条边相等的四边形是菱形
C.对角线互相垂直的平行四边形是菱形
D.对角线互相垂直平分的四边形是菱形
B
4. 如图所示,在 ABCD中,AB=13,AC=10,当BD= 时,四边形ABCD是菱形.
24
5.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的
平分线交BC于点E,连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.
(1)证明:由尺规作∠BAF的平分线的过程可得AB=AF,∠BAE=∠FAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠FAE=∠AEB,
∴∠BAE=∠AEB,∴AB=BE,
∴BE=FA,∴四边形ABEF为平行四边形,
∵AB=AF,
∴四边形ABEF为菱形.
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.
(2)∵四边形ABEF为菱形,
∴AE⊥BF,BO= FB=3,AE=2AO,
在Rt△AOB中,由勾股定理得AO =4,
∴AE=2AO=8.
6. 如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.
求证:四边形ACFD是菱形.
证明:由平移变换的性质得CF=AD=10cm,DF=AC.
∵∠B=90°,AB=6cm,BC=8cm,
∴AC=DF=AD=CF=10cm,
∴四边形ACFD是菱形.
课堂小结
一组邻边相等
对角线互相垂直
四条边相等
五种判定方法
四边形
平行四边形
菱形
菱形的判定方法:
第19章 四边形
19.3.2 第2课时 菱形的判定
知识回顾
菱形的定义是什么?性质有哪些?
一组邻边相等
有一组邻边相等的平行四边形叫做菱形
平行四边形
菱形
菱形的性质
菱形的四条边都相等
菱形的两组对边分别平行
菱形的两条对角线互相平分
边
对角线
角
菱形的两组对角分别相等
菱形的邻角分别互补
菱形的两条对角线互相垂直
菱形的每一条对角线平分一组对角
菱形
获取新知
知识点一:定义判定法
根据菱形的定义,可得菱形的第一个判定的方法:
∵四边形ABCD是平行四边形,
AB=AD,
∴四边形ABCD是菱形.
符号语言
有一组邻边相等的平行四边形叫做菱形.
A
B
C
D
知识点二:边判定法
已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗?
C
A
B
D
小刚:分别以A、C为圆心,以大于 AC的长为半径作弧,两条 弧分别相交于点B , D,依次连接A、B、C、D四点.
你觉得小刚的做法对吗?为什么?
判定定理1:四边都相等的四边形是菱形
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
A
B
C
D
证明:∵AB=BC=CD=AD;
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.
四条边都相等的四边形是菱形
AB=BC=CD=AD
∵在四边形ABCD中,AB=BC=CD=AD,
∴四边形 ABCD是菱形.
A
B
C
D
菱形ABCD
菱形的判定定理:
四边形ABCD
A
B
C
D
符号语言:
例题讲解
例1 如图,顺次连接对角线相等的四边形ABCD各边中点,得到四边形EFGH是什么四边形?
解:四边形EFGH是菱形.
又∵AC=BD,
∵点E、F、G、H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
理由如下:连接AC、BD
∴EF=GH= BD, FG=HE= AC,
C
A
B
D
E
F
G
H
知识点二:对角线判定法
前面我们用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形.那么转动木条,这个平行四边形什么时候变成菱形 对此你有什么猜想?
获取新知
判定定理2:对角线互相垂直的平行四边形是菱形.
已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O ,AC⊥BD.
求证:□ABCD是菱形.
A
B
C
O
D
证明: ∵四边形ABCD是平行四边形.
∴OA=OC.
又∵AC⊥BD,
∴BD是线段AC的垂直平分线.
∴BA=BC.
∴四边形ABCD是菱形(菱形的定义).
对角线互相垂直的平行四边形是菱形.
AC⊥BD
∵在□ABCD中,AC⊥BD,
∴ □ABCD是菱形.
符号语言:
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
菱形的判定定理:
例题讲解
例2 如图,在 ABCD中,AC=8,BD=6,AB=5,
求AD的长.
A
B
C
D
O
解:∵四边形ABCD是平行四边形,
∴OA= AC=4,OB= BD=3.
又∵AB=5,满足AB2=OA2+OB2,
∴△AOB为直角三角形,及OA⊥OB.
∴ ABCD是菱形,AD=AB=5.
归纳对比
随堂演练
1. 如图,要使 ABCD成为菱形,则需添加的一个条件可以是( )
A. AC=AD B. BA=BC
C. ∠ABC=90° D. AC=BD
B
2. 下列命题中,正确的是( )
A.对角线相等的四边形是菱形
B.对角线互相垂直的四边形是菱形
C.对角线相等的平行四边形是菱形
D.对角线互相垂直的平行四边形是菱形
D
3. 如图,已知△ABC,AB=AC,将△ABC沿边BC翻折,得到的△DBC与原△ABC拼成四边形ABDC,则能直接判定四边形ABDC是菱形的依据是( )
A.一组邻边相等的平行四边形是菱形
B.四条边相等的四边形是菱形
C.对角线互相垂直的平行四边形是菱形
D.对角线互相垂直平分的四边形是菱形
B
4. 如图所示,在 ABCD中,AB=13,AC=10,当BD= 时,四边形ABCD是菱形.
24
5.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的
平分线交BC于点E,连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.
(1)证明:由尺规作∠BAF的平分线的过程可得AB=AF,∠BAE=∠FAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠FAE=∠AEB,
∴∠BAE=∠AEB,∴AB=BE,
∴BE=FA,∴四边形ABEF为平行四边形,
∵AB=AF,
∴四边形ABEF为菱形.
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.
(2)∵四边形ABEF为菱形,
∴AE⊥BF,BO= FB=3,AE=2AO,
在Rt△AOB中,由勾股定理得AO =4,
∴AE=2AO=8.
6. 如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.
求证:四边形ACFD是菱形.
证明:由平移变换的性质得CF=AD=10cm,DF=AC.
∵∠B=90°,AB=6cm,BC=8cm,
∴AC=DF=AD=CF=10cm,
∴四边形ACFD是菱形.
课堂小结
一组邻边相等
对角线互相垂直
四条边相等
五种判定方法
四边形
平行四边形
菱形
菱形的判定方法:
