沪科版数学八年级下册 19.3.3 正方形 同步课件 (共25张PPT)
文档属性
| 名称 | 沪科版数学八年级下册 19.3.3 正方形 同步课件 (共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 947.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 07:06:30 | ||
图片预览





文档简介
(共25张PPT)
第19章 四边形
19.3.3 正方形
知识回顾
问题1 平行四边形、矩形、菱形都各有哪些性质?
平行四边形
边:
角:
对角线:
对边平行且相等
对角相等,邻角互补
对角线互相平分
矩形
角:
四个角是直角
对角线:
对角线相等
边:
同上
具有平行四边形所有性质
菱形的性质
菱形的性质
边:
四条边相等
对角线:
互相垂直平分
分别平分两组对角
同上
具有平行四边形一切性质
角:
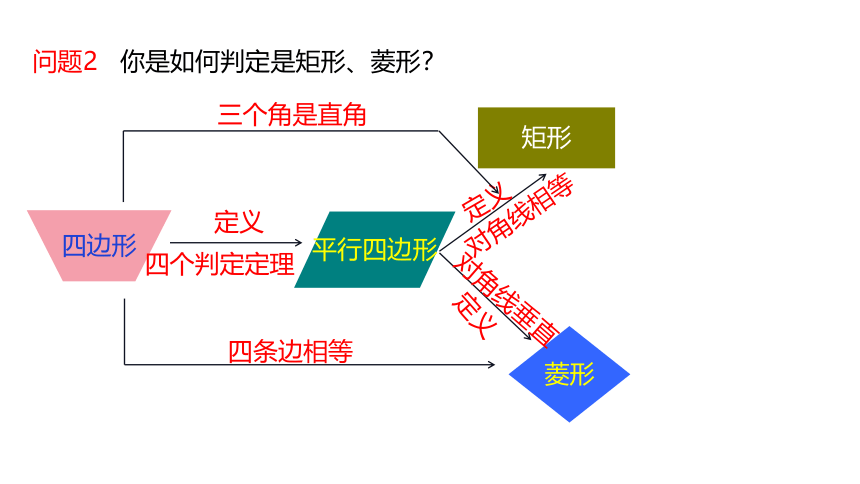
问题2 你是如何判定是矩形、菱形?
平行四边形
矩形
菱形
四边形
三个角是直角
四条边相等
定义
四个判定定理
定义
对角线相等
定义
对角线垂直
情景导入
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
你还能举出其他的例子吗?
获取新知
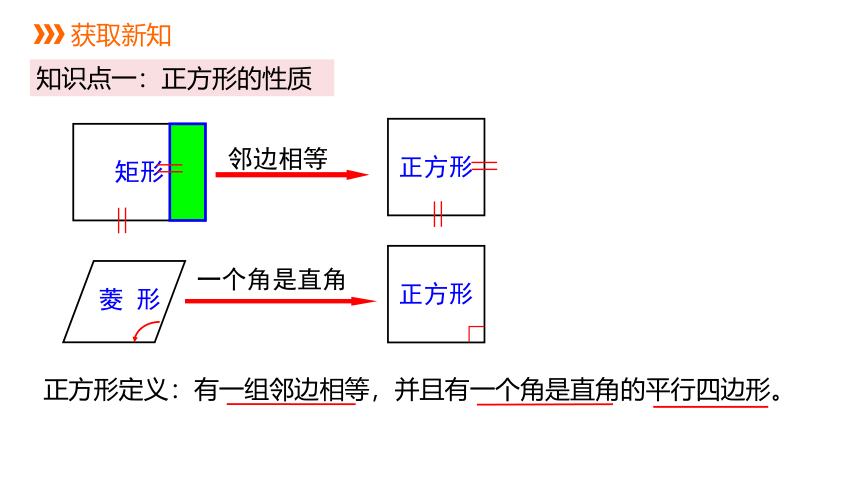
知识点一:正方形的性质
邻边相等
矩形
正方形
菱 形
一个角是直角
正方形
∟
正方形定义:有一组邻边相等,并且有一个角是直角的平行四边形。
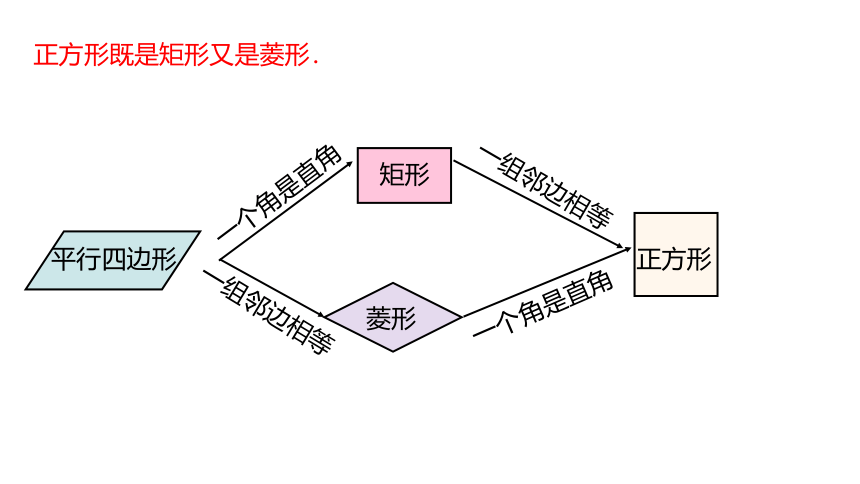
正方形既是矩形又是菱形.
一个角是直角
一组邻边相等
平行四边形
矩形
菱形
一组邻边相等
一个角是直角
正方形
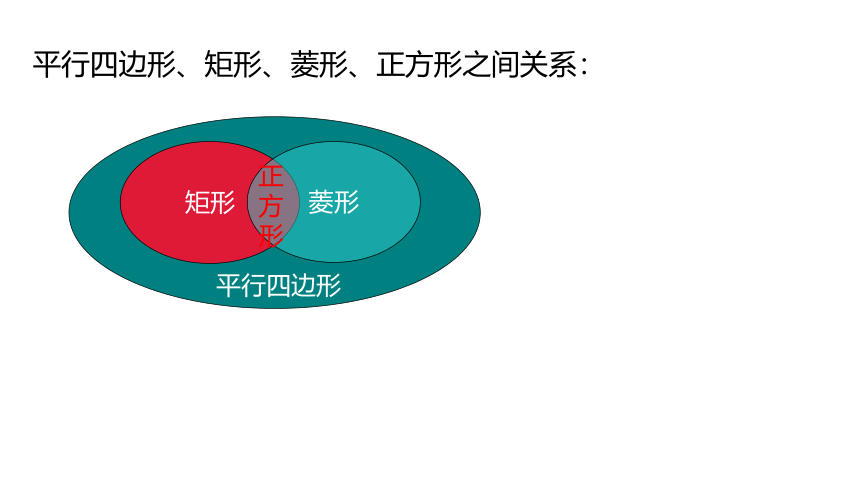
平行四边形、矩形、菱形、正方形之间关系:
矩形
菱形
正
方
形
平行四边形
正方形是特殊的矩形,也是特殊的菱形,更是特殊的平行四边形.所以矩形、菱形有的性质,正方形都有.
性质:1.正方形的四个角都是直角;
2.四条边相等,对边平行;
3.正方形的对角线相等且互相垂直平分.
例题讲解
例1 求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知: 如图,四边形ABCD是正方形,对角线AC、BD相交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
A
D
C
B
O
A
D
C
B
O
证明: ∵ 四边形ABCD是正方形,
∴ AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都
是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO.
知识点二:正方形的判定
正方形是特殊的矩形,也是特殊的菱形,更是特殊的平行四边形.所以有:
正方形
+
先判定菱形
矩形条件(二选一)
一个直角
对角线相等
正方形
+
先判定矩形
菱形条件(二选一)
一组邻边相等
对角线垂直
平行四边形
一组邻边相等
一内角是直角
正方形
例题讲解
例2 如图,点A′,B′,C′,D′分别是正方形ABCD
四条边上的点,并且AA′=BB′=CC′=DD′.
求证:四边形A′B′C′D′是正方形.
分析:由已知可证△AEN≌△BFE≌△CMF≌△DNM,得四边形EFMN是菱形,再证有一个角是直角即可.
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,
∴AN=BE=CF=DM.
∴△AEN≌△BFE≌△CMF≌△DNM(SAS),
∴EN=FE=MF=NM,∠ANE=∠BEF,
∴四边形EFMN是菱形,
∠NEF=180°-(∠AEN+∠BEF)
=180°-(∠AEN+∠ANE)
=180°-90°=90°.
∴四边形EFMN是正方形 .
随堂演练
1.正方形具有而矩形不一定具有的性质是 ( )
A.四个角相等
B.对角线互相垂直平分
C.对角互补
D.对角线相等
B
2. 平行四边形、矩形、菱形、正方形共有的性质是( )
A.对角线相等
B.对角线互相平分
C.对角线互相垂直
D.对角形互相垂直平分
B
3. 如图,已知P是正方形ABCD的对角线BD上一点,且BP=BC,则∠ACP的度数是( )
A.45° B.22.5°
C.67.5° D.75°
B
4.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,
③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,其中正确的是______________________(只填写序号).
①③或①②或④②或④③
5. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且BE=CF.
求证:(1)△ABE≌△BCF;
(2)AE⊥BF.
证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠C=90°.
在△ABE和△BCF中,AB=BC,∠ABE=∠C, BE=CF
∴△ABE≌△BCF.
(2)如图,设AE与BF交于点O.
∵△ABE≌△BCF,
∴∠BAE=∠CBF.
∵∠ABE=90°,
∴∠BAE+∠AEB=90°,
∴∠CBF+∠AEB=90°,
∴∠BOE=90°,即AE⊥BF.
6. 已知:如图,在△ABC中,AB=AC,D是BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
证明:(1)∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵AB=AC,∴∠B=∠C.
∵D是BC边的中点,
∴BD=CD,
∴△BED≌△CFD.
(2)∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
又∵∠A=90°,
∴四边形DFAE是矩形.
∵△BED≌△CFD,
∴DE=DF,∴矩形DFAE是正方形.
课堂小结
正方形的性质
四条边都相等
两组对边分别平行
两条对角线互相平分
边
对角线
角
两组对角分别相等,邻角分别互补
四个角都是直角
两条对角线互相垂直,每一条对角线平分一组对角
对角线相等
正方形
5种识别方法
三个角是直角
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
四边形
平行四边形
矩形
菱形
正方形
正方形的判定
四条边都相等
第19章 四边形
19.3.3 正方形
知识回顾
问题1 平行四边形、矩形、菱形都各有哪些性质?
平行四边形
边:
角:
对角线:
对边平行且相等
对角相等,邻角互补
对角线互相平分
矩形
角:
四个角是直角
对角线:
对角线相等
边:
同上
具有平行四边形所有性质
菱形的性质
菱形的性质
边:
四条边相等
对角线:
互相垂直平分
分别平分两组对角
同上
具有平行四边形一切性质
角:
问题2 你是如何判定是矩形、菱形?
平行四边形
矩形
菱形
四边形
三个角是直角
四条边相等
定义
四个判定定理
定义
对角线相等
定义
对角线垂直
情景导入
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
你还能举出其他的例子吗?
获取新知
知识点一:正方形的性质
邻边相等
矩形
正方形
菱 形
一个角是直角
正方形
∟
正方形定义:有一组邻边相等,并且有一个角是直角的平行四边形。
正方形既是矩形又是菱形.
一个角是直角
一组邻边相等
平行四边形
矩形
菱形
一组邻边相等
一个角是直角
正方形
平行四边形、矩形、菱形、正方形之间关系:
矩形
菱形
正
方
形
平行四边形
正方形是特殊的矩形,也是特殊的菱形,更是特殊的平行四边形.所以矩形、菱形有的性质,正方形都有.
性质:1.正方形的四个角都是直角;
2.四条边相等,对边平行;
3.正方形的对角线相等且互相垂直平分.
例题讲解
例1 求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
已知: 如图,四边形ABCD是正方形,对角线AC、BD相交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
A
D
C
B
O
A
D
C
B
O
证明: ∵ 四边形ABCD是正方形,
∴ AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都
是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO.
知识点二:正方形的判定
正方形是特殊的矩形,也是特殊的菱形,更是特殊的平行四边形.所以有:
正方形
+
先判定菱形
矩形条件(二选一)
一个直角
对角线相等
正方形
+
先判定矩形
菱形条件(二选一)
一组邻边相等
对角线垂直
平行四边形
一组邻边相等
一内角是直角
正方形
例题讲解
例2 如图,点A′,B′,C′,D′分别是正方形ABCD
四条边上的点,并且AA′=BB′=CC′=DD′.
求证:四边形A′B′C′D′是正方形.
分析:由已知可证△AEN≌△BFE≌△CMF≌△DNM,得四边形EFMN是菱形,再证有一个角是直角即可.
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠A=∠B=∠C=∠D=90°.
∵AE=BF=CM=DN,
∴AN=BE=CF=DM.
∴△AEN≌△BFE≌△CMF≌△DNM(SAS),
∴EN=FE=MF=NM,∠ANE=∠BEF,
∴四边形EFMN是菱形,
∠NEF=180°-(∠AEN+∠BEF)
=180°-(∠AEN+∠ANE)
=180°-90°=90°.
∴四边形EFMN是正方形 .
随堂演练
1.正方形具有而矩形不一定具有的性质是 ( )
A.四个角相等
B.对角线互相垂直平分
C.对角互补
D.对角线相等
B
2. 平行四边形、矩形、菱形、正方形共有的性质是( )
A.对角线相等
B.对角线互相平分
C.对角线互相垂直
D.对角形互相垂直平分
B
3. 如图,已知P是正方形ABCD的对角线BD上一点,且BP=BC,则∠ACP的度数是( )
A.45° B.22.5°
C.67.5° D.75°
B
4.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,
③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,其中正确的是______________________(只填写序号).
①③或①②或④②或④③
5. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且BE=CF.
求证:(1)△ABE≌△BCF;
(2)AE⊥BF.
证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠C=90°.
在△ABE和△BCF中,AB=BC,∠ABE=∠C, BE=CF
∴△ABE≌△BCF.
(2)如图,设AE与BF交于点O.
∵△ABE≌△BCF,
∴∠BAE=∠CBF.
∵∠ABE=90°,
∴∠BAE+∠AEB=90°,
∴∠CBF+∠AEB=90°,
∴∠BOE=90°,即AE⊥BF.
6. 已知:如图,在△ABC中,AB=AC,D是BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
证明:(1)∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°.
∵AB=AC,∴∠B=∠C.
∵D是BC边的中点,
∴BD=CD,
∴△BED≌△CFD.
(2)∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°.
又∵∠A=90°,
∴四边形DFAE是矩形.
∵△BED≌△CFD,
∴DE=DF,∴矩形DFAE是正方形.
课堂小结
正方形的性质
四条边都相等
两组对边分别平行
两条对角线互相平分
边
对角线
角
两组对角分别相等,邻角分别互补
四个角都是直角
两条对角线互相垂直,每一条对角线平分一组对角
对角线相等
正方形
5种识别方法
三个角是直角
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
四边形
平行四边形
矩形
菱形
正方形
正方形的判定
四条边都相等
