沪科版数学八年级下册20.2.2.1方差 同步课件 (共20张PPT)
文档属性
| 名称 | 沪科版数学八年级下册20.2.2.1方差 同步课件 (共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 07:07:29 | ||
图片预览






文档简介
(共20张PPT)
第20章 数据的初步分析
20.2.2 第1课时 方差
情景导入
2020年我校篮球联赛开始了
刘教练
选 我
选 我
教练的烦恼
?
观察对比两幅图片,哪个队站得更整齐?
我们常用平均数、中位数来刻画数据的“集中水平”,但在有些情况下只有“集中水平”是不够的,如评价选手的射击水平、机器的加工零件的精度、手表的日走时误差时,还需要用一新的数来刻画一组数据的波动情况.
获取新知
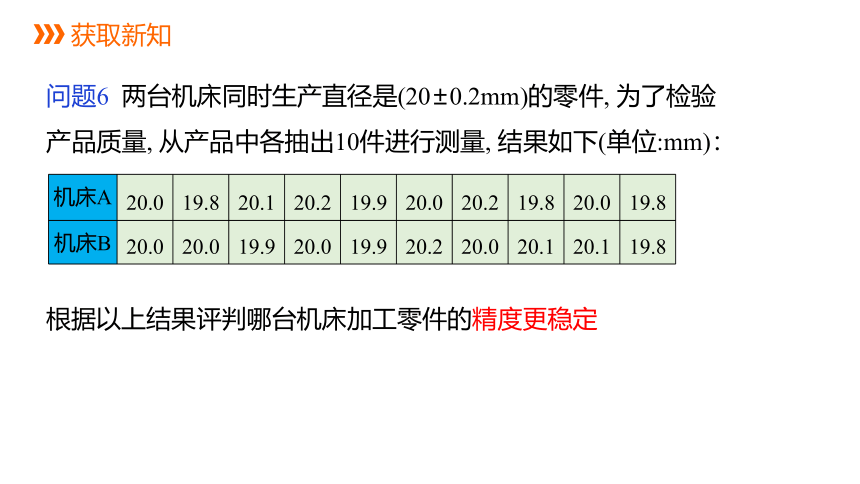
问题6 两台机床同时生产直径是(20±0.2mm)的零件, 为了检验产品质量, 从产品中各抽出10件进行测量, 结果如下(单位:mm):
机床A 20.0 19.8 20.1 20.2 19.9 20.0 20.2 19.8 20.0 19.8
机床B 20.0 20.0 19.9 20.0 19.9 20.2 20.0 20.1 20.1 19.8
根据以上结果评判哪台机床加工零件的精度更稳定
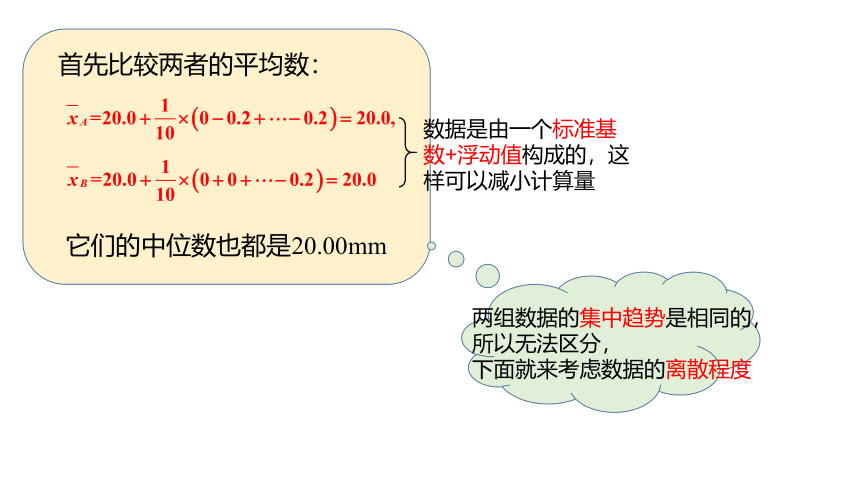
首先比较两者的平均数:
它们的中位数也都是20.00mm
数据是由一个标准基数+浮动值构成的,这样可以减小计算量
两组数据的集中趋势是相同的,所以无法区分,
下面就来考虑数据的离散程度
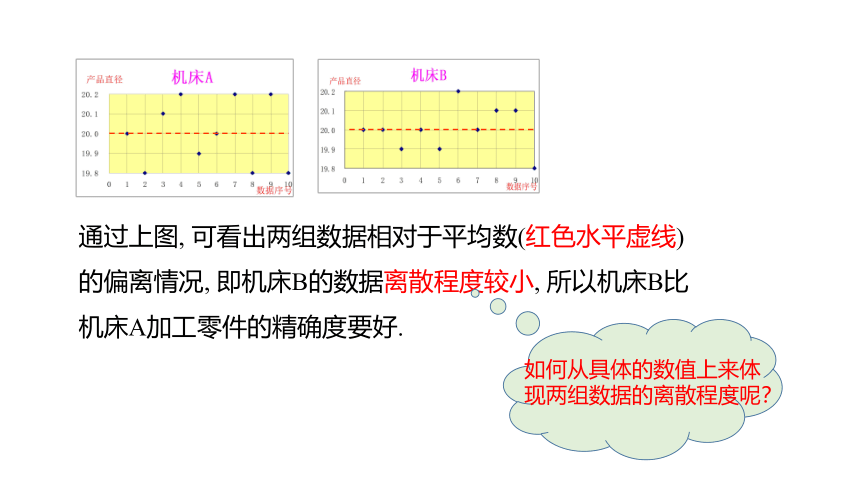
通过上图, 可看出两组数据相对于平均数(红色水平虚线)的偏离情况, 即机床B的数据离散程度较小, 所以机床B比机床A加工零件的精确度要好.
如何从具体的数值上来体现两组数据的离散程度呢?
1.统计中常采用下面的做法:设一组数据x1, x2 ,… ,xn,它们的平均数是各数是 ,我们用
来衡量这组数据的离散程度,并把它叫做这组数据的方差.
2.方差的意义:
方差越大,数据的波动越大,越离散,越不稳定;
方差越小,数据的波动越小,越集中,越稳定.
下面通过计算方差,来评判问题中机床A和机床B哪台生产的零件的精度更稳定:
两组数据的方差分别是:
显然 > ,即可知机床A生产的10个零件直径比机床B生产的10个零件直径波动要大
例题讲解
例 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》, 参加表演的女演员的身高(单位:cm)如表所示.
哪个芭蕾舞团女演员的身高更整齐?
甲 163 164 164 165 165 166 166 167
乙 163 165 165 166 166 167 168 168
解:甲、乙两团演员的身高平均数分别是
方差分别是
由s甲2 < s乙2 可知,甲芭蕾舞团女演员的身高更整齐.
原始数据x1, x2 ,… ,xn
构造数据x1±b, x2±b ,… ,xn±b
原始数据ax1,ax2 ,… ,axn
构造数据ax1±b, ax2±b ,… ,axn±b
平均数
方差
方差的变化规律
随堂演练
1. 在方差的计算公式 中,数10和20分别表示( )
A.数据的个数和方差
B.数据的个数和平均数
C.平均数和数据的个数
D.数据的方差和平均数
B
2. 某排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194.现用一名身高为186 cm的队员换下场上身高为192 cm的队员,与换人前相比,场上队员身高的( )
A.平均数变小,方差变小
B.平均数变小,方差变大
C.平均数变大,方差变小
D.平均数变大,方差变大
A
3.如图是一次射击训练中甲、乙两人的10次射击成绩的分布情况,则射击成绩的方差较小的是 .(填“甲”或“乙”)
甲
4. 已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是 ,那么另一组数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的平均数为 和方差为_____
4
3
5.为了从甲、乙两名学生中选择一人去参加电脑知识竞赛,在相同条件下对他们的电脑知识进行10次测验,成绩(单位:分)如下:
甲的成绩 76 84 90 84 81 87 88 81 85 84
乙的成绩 82 86 87 90 79 81 93 90 74 78
(1)填写下表:
同学 平均成绩 中位数 众数 方差 85分以上的频率
甲 84 84 0.3
乙 84 84 34
84
90
0.5
14.4
(2)利用以上信息,请从不同的角度对甲、乙两名同学的成绩进行评价.
解:从众数看,甲成绩的众数为84分,乙成绩的众数是90分,乙的成绩比甲好;
从方差看,s2甲=14.4, s2乙=34,甲的成绩比乙相对稳定;从甲、乙的中位数、平均数看,中位数、平均数都是84分,两人成绩一样好;
从频率看,甲85分以上的次数比乙少,乙的成绩比甲好.
课堂小结
方差
方差的统计学意义(判断数据的波动程度):
方差越大(小),数据的波动越大(小).
公式:
第20章 数据的初步分析
20.2.2 第1课时 方差
情景导入
2020年我校篮球联赛开始了
刘教练
选 我
选 我
教练的烦恼
?
观察对比两幅图片,哪个队站得更整齐?
我们常用平均数、中位数来刻画数据的“集中水平”,但在有些情况下只有“集中水平”是不够的,如评价选手的射击水平、机器的加工零件的精度、手表的日走时误差时,还需要用一新的数来刻画一组数据的波动情况.
获取新知
问题6 两台机床同时生产直径是(20±0.2mm)的零件, 为了检验产品质量, 从产品中各抽出10件进行测量, 结果如下(单位:mm):
机床A 20.0 19.8 20.1 20.2 19.9 20.0 20.2 19.8 20.0 19.8
机床B 20.0 20.0 19.9 20.0 19.9 20.2 20.0 20.1 20.1 19.8
根据以上结果评判哪台机床加工零件的精度更稳定
首先比较两者的平均数:
它们的中位数也都是20.00mm
数据是由一个标准基数+浮动值构成的,这样可以减小计算量
两组数据的集中趋势是相同的,所以无法区分,
下面就来考虑数据的离散程度
通过上图, 可看出两组数据相对于平均数(红色水平虚线)的偏离情况, 即机床B的数据离散程度较小, 所以机床B比机床A加工零件的精确度要好.
如何从具体的数值上来体现两组数据的离散程度呢?
1.统计中常采用下面的做法:设一组数据x1, x2 ,… ,xn,它们的平均数是各数是 ,我们用
来衡量这组数据的离散程度,并把它叫做这组数据的方差.
2.方差的意义:
方差越大,数据的波动越大,越离散,越不稳定;
方差越小,数据的波动越小,越集中,越稳定.
下面通过计算方差,来评判问题中机床A和机床B哪台生产的零件的精度更稳定:
两组数据的方差分别是:
显然 > ,即可知机床A生产的10个零件直径比机床B生产的10个零件直径波动要大
例题讲解
例 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》, 参加表演的女演员的身高(单位:cm)如表所示.
哪个芭蕾舞团女演员的身高更整齐?
甲 163 164 164 165 165 166 166 167
乙 163 165 165 166 166 167 168 168
解:甲、乙两团演员的身高平均数分别是
方差分别是
由s甲2 < s乙2 可知,甲芭蕾舞团女演员的身高更整齐.
原始数据x1, x2 ,… ,xn
构造数据x1±b, x2±b ,… ,xn±b
原始数据ax1,ax2 ,… ,axn
构造数据ax1±b, ax2±b ,… ,axn±b
平均数
方差
方差的变化规律
随堂演练
1. 在方差的计算公式 中,数10和20分别表示( )
A.数据的个数和方差
B.数据的个数和平均数
C.平均数和数据的个数
D.数据的方差和平均数
B
2. 某排球队6名场上队员的身高(单位:cm)是:180,184,188,190,192,194.现用一名身高为186 cm的队员换下场上身高为192 cm的队员,与换人前相比,场上队员身高的( )
A.平均数变小,方差变小
B.平均数变小,方差变大
C.平均数变大,方差变小
D.平均数变大,方差变大
A
3.如图是一次射击训练中甲、乙两人的10次射击成绩的分布情况,则射击成绩的方差较小的是 .(填“甲”或“乙”)
甲
4. 已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是 ,那么另一组数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的平均数为 和方差为_____
4
3
5.为了从甲、乙两名学生中选择一人去参加电脑知识竞赛,在相同条件下对他们的电脑知识进行10次测验,成绩(单位:分)如下:
甲的成绩 76 84 90 84 81 87 88 81 85 84
乙的成绩 82 86 87 90 79 81 93 90 74 78
(1)填写下表:
同学 平均成绩 中位数 众数 方差 85分以上的频率
甲 84 84 0.3
乙 84 84 34
84
90
0.5
14.4
(2)利用以上信息,请从不同的角度对甲、乙两名同学的成绩进行评价.
解:从众数看,甲成绩的众数为84分,乙成绩的众数是90分,乙的成绩比甲好;
从方差看,s2甲=14.4, s2乙=34,甲的成绩比乙相对稳定;从甲、乙的中位数、平均数看,中位数、平均数都是84分,两人成绩一样好;
从频率看,甲85分以上的次数比乙少,乙的成绩比甲好.
课堂小结
方差
方差的统计学意义(判断数据的波动程度):
方差越大(小),数据的波动越大(小).
公式:
