沪科版数学七年级下册 7.4 综合与实践 排队问题 课件(共16张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 7.4 综合与实践 排队问题 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 07:10:02 | ||
图片预览





文档简介
(共14张PPT)
7.4 综合与实践
———— 排队问题
大家见过这个标志吗?
它表示什么意思?
首都文明办主任——张慧光介绍,无论上车、办事,两人以上就应该像“11”一样顺序排队,有序进行,所以把每月的11日定为排队日,是对国民公共礼仪的一种善意提醒。
某服务机构开设了一个窗口办理业务,并按“先到达,先服务 ”的方式服务,该窗口每2min服务一名顾客,已知当窗口开始工作时,已有5名顾客在等待,在窗口开始工作1min后,又有一位"新顾客”到达,且预计以后每5min都有一位“新顾客”到达。
问题
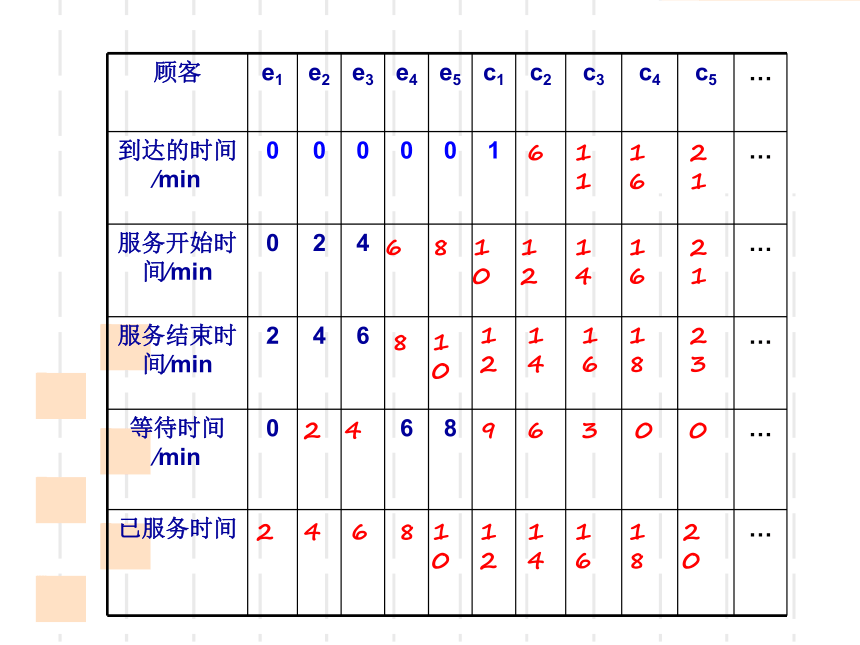
(1)设e1,e2,e3,…,e5表示当窗口开始工作时已经在等待的5位顾客,c1,c2,c3,…,cn表示在窗口开始工作后,按先后顺序到达的“新顾客 ”,请将下面表格补充完整(这里假设e1,e2,e3,…,e5的到达时间为0)
顾客 e1 e2 e3 e4 e5 c1 c2 c3 c4 c5 …
到达的时间∕min 0 0 0 0 0 1 …
服务开始时间∕min 0 2 4 …
服务结束时间∕min 2 4 6 …
等待时间∕min
0 6 8 …
已服务时间 …
6
11
16
21
6
8
10
12
14
16
21
8
10
12
14
16
18
23
2
4
9
6
3
0
0
2
4
6
8
10
12
14
16
18
20
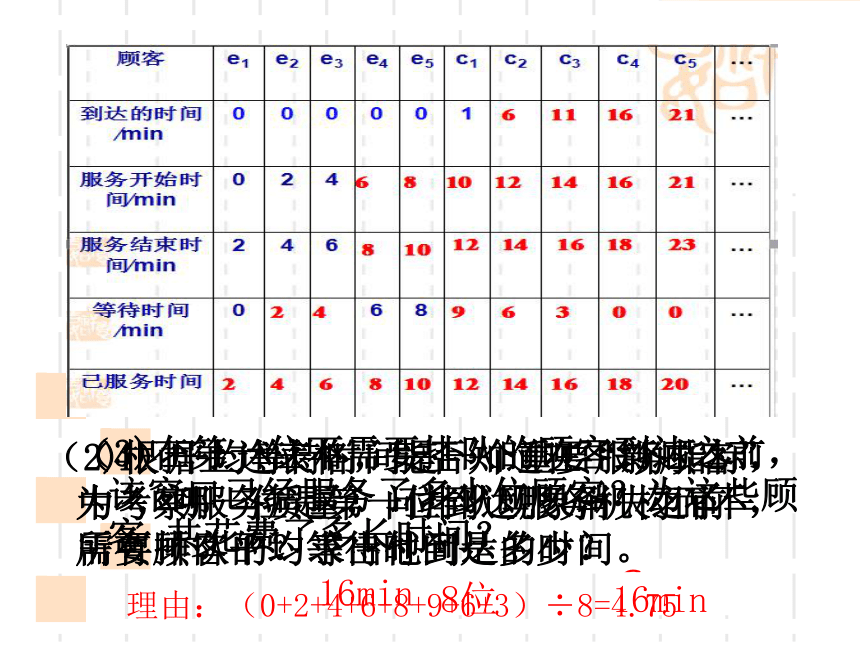
(2)根据上述表格,能否知道在“新顾客”中 ,哪一位是第一位到达服务机构而不需要排队的?求出他到达的时间。
16min
c4
(3)在第一位不需要排队的顾客到达之前,该窗口已经服务了多少位顾客?为这些顾客 共花费了多长时间?
8位
16min
(4)平均等待时间是一个重要服务指标,为考察服务质量,问排队现象消失之前 ,所有顾客平均等待时间是多少?
理由:(0+2+4+6+8+9+6+3)÷8=4.75
探究:
在上述问题中,如果问题的条件变复杂(例如:当窗口开始工作时已经在等待的顾客非常多),使用列表方法就很不方便,你能否用代数式表示上面的数量,总结上面表格中的数量关系,并根据这个关系来解决问题?
顾客 e1 e2 e3 e4 e5 c1 c2 c3 c4 c5 … cn Cn+1
到达的时间∕min 0 0 0 0 0 1 …
服务开始时间∕min 0 2 4 …
服务结束时间∕min 2 4 6 …
等待时间∕min
0 6 8 …
已服务时间 …
6
11
16
21
5n-4
5n+1
6
8
10
12
14
16
21
8
10
12
14
16
18
23
2
4
9
6
3
0
0
2
4
6
8
10
12
14
16
18
20
5n-4
5n+1
5n-2
5n+3
0
0
2(n+5)
2(n+6)
结论
在排队消失之前,该窗口为顾客服务花费的时间小于等于第一位到达后不需要排队的“新顾客”到达时间
2(n+5)≤ 5n+1
n≥3
所以 = 即从第4位“新顾客” 开始排队消失
在上述条件下,把已经有5位顾客在等待
改为已经有10位顾客在等待(其他条件不变)
且当“新顾客” 离去时,排队现象消失了,
即 为第一位到达后不需要排队 的新顾客
问:
探究:
某服务机构开设了一个窗口办理业务,并按“先到达,先服务 ”的方式服务,该窗口每2min服务一名顾客,已知当窗口开始工作时,已有5名顾客在等待,在窗口开始工作1min后,又有一位"新顾客”到达,且预计以后每5min都有一位“新顾客”到达。
(3)根据(1)和(2)得到的代数式以及它们的数量关系求n+1的值
n+1=8
(2)用关于n的代数式表示 的到达时间?
5n+1
(1)用关于n的代数式来表示,在第一位不
需要排队的新顾客 到达之前,该窗口
已经服务了多少位顾客?为这些顾客服务共
花费了多少时间?
10+n
2(n+10)
课后探究
改变问题中的条件:
第一组:将该服务窗口每2min服务一位顾客改为每 5min服务一位顾客 (其它条件不变)
第二组:在窗口开始工作1min后又有位“新顾客”到达 改为在窗口开始工作2min后又有位“新顾客”到达 (其它条件不变)
第三组:预计以后每5min都有一位“新顾客”到达改为预计以后每2min都有一位“新顾客”到达(其它条件不变)
小结
1、通过本节课的学习,你有什么收获?你 认为总结规律的一般方法是什么?
2、希望同学们在以后的学习中能积极参与数学实践活动中来,主动探索,积极思考,我相信同学们在参与活动的过程中一定会有所收获。
7.4 综合与实践
———— 排队问题
大家见过这个标志吗?
它表示什么意思?
首都文明办主任——张慧光介绍,无论上车、办事,两人以上就应该像“11”一样顺序排队,有序进行,所以把每月的11日定为排队日,是对国民公共礼仪的一种善意提醒。
某服务机构开设了一个窗口办理业务,并按“先到达,先服务 ”的方式服务,该窗口每2min服务一名顾客,已知当窗口开始工作时,已有5名顾客在等待,在窗口开始工作1min后,又有一位"新顾客”到达,且预计以后每5min都有一位“新顾客”到达。
问题
(1)设e1,e2,e3,…,e5表示当窗口开始工作时已经在等待的5位顾客,c1,c2,c3,…,cn表示在窗口开始工作后,按先后顺序到达的“新顾客 ”,请将下面表格补充完整(这里假设e1,e2,e3,…,e5的到达时间为0)
顾客 e1 e2 e3 e4 e5 c1 c2 c3 c4 c5 …
到达的时间∕min 0 0 0 0 0 1 …
服务开始时间∕min 0 2 4 …
服务结束时间∕min 2 4 6 …
等待时间∕min
0 6 8 …
已服务时间 …
6
11
16
21
6
8
10
12
14
16
21
8
10
12
14
16
18
23
2
4
9
6
3
0
0
2
4
6
8
10
12
14
16
18
20
(2)根据上述表格,能否知道在“新顾客”中 ,哪一位是第一位到达服务机构而不需要排队的?求出他到达的时间。
16min
c4
(3)在第一位不需要排队的顾客到达之前,该窗口已经服务了多少位顾客?为这些顾客 共花费了多长时间?
8位
16min
(4)平均等待时间是一个重要服务指标,为考察服务质量,问排队现象消失之前 ,所有顾客平均等待时间是多少?
理由:(0+2+4+6+8+9+6+3)÷8=4.75
探究:
在上述问题中,如果问题的条件变复杂(例如:当窗口开始工作时已经在等待的顾客非常多),使用列表方法就很不方便,你能否用代数式表示上面的数量,总结上面表格中的数量关系,并根据这个关系来解决问题?
顾客 e1 e2 e3 e4 e5 c1 c2 c3 c4 c5 … cn Cn+1
到达的时间∕min 0 0 0 0 0 1 …
服务开始时间∕min 0 2 4 …
服务结束时间∕min 2 4 6 …
等待时间∕min
0 6 8 …
已服务时间 …
6
11
16
21
5n-4
5n+1
6
8
10
12
14
16
21
8
10
12
14
16
18
23
2
4
9
6
3
0
0
2
4
6
8
10
12
14
16
18
20
5n-4
5n+1
5n-2
5n+3
0
0
2(n+5)
2(n+6)
结论
在排队消失之前,该窗口为顾客服务花费的时间小于等于第一位到达后不需要排队的“新顾客”到达时间
2(n+5)≤ 5n+1
n≥3
所以 = 即从第4位“新顾客” 开始排队消失
在上述条件下,把已经有5位顾客在等待
改为已经有10位顾客在等待(其他条件不变)
且当“新顾客” 离去时,排队现象消失了,
即 为第一位到达后不需要排队 的新顾客
问:
探究:
某服务机构开设了一个窗口办理业务,并按“先到达,先服务 ”的方式服务,该窗口每2min服务一名顾客,已知当窗口开始工作时,已有5名顾客在等待,在窗口开始工作1min后,又有一位"新顾客”到达,且预计以后每5min都有一位“新顾客”到达。
(3)根据(1)和(2)得到的代数式以及它们的数量关系求n+1的值
n+1=8
(2)用关于n的代数式表示 的到达时间?
5n+1
(1)用关于n的代数式来表示,在第一位不
需要排队的新顾客 到达之前,该窗口
已经服务了多少位顾客?为这些顾客服务共
花费了多少时间?
10+n
2(n+10)
课后探究
改变问题中的条件:
第一组:将该服务窗口每2min服务一位顾客改为每 5min服务一位顾客 (其它条件不变)
第二组:在窗口开始工作1min后又有位“新顾客”到达 改为在窗口开始工作2min后又有位“新顾客”到达 (其它条件不变)
第三组:预计以后每5min都有一位“新顾客”到达改为预计以后每2min都有一位“新顾客”到达(其它条件不变)
小结
1、通过本节课的学习,你有什么收获?你 认为总结规律的一般方法是什么?
2、希望同学们在以后的学习中能积极参与数学实践活动中来,主动探索,积极思考,我相信同学们在参与活动的过程中一定会有所收获。
