人教版八年级数学 下册 20.1.1 .1加权平均数 课件(共25张PPT)
文档属性
| 名称 | 人教版八年级数学 下册 20.1.1 .1加权平均数 课件(共25张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 440.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 07:20:04 | ||
图片预览







文档简介
(共25张PPT)
温故知新:
数据2、3、4、1、2的
平均数是________,这个
平均数叫做_________平
均数.
2.4
算术
20.1.1 平均数
第1课时 加权平均数
人教版八年级数学 下册
学习目标:
1.理解加权平均数的意义;
2.会用加权平均数分析一组数据的集中趋势,发展数据分析能力。
一次数学测验,3名同学的数学成绩分别是60,80和100分,则他们的平均成绩是多少?你怎样列式计算?算式中的分子分母分别表示什么含义?
平均数是一组数据的数值的代表值,它刻画了这组数据整体的平均状态.
如果有n个数(用χ1、χ2、χ3、…χn)那么它们的平均数我们表示为
80
x1 + x2 +… + xn
n
x =
x =
探究问题
如果知道有一个小组中3名学生得了60分,5名学生得了80分,还有一名学生得了100分,此时这个小组的数学测验平均分还是一问中的答案吗?该如何计算呢?
≈75.6
日常生活中,我们常用平均数表示一组数据的“平均水平”
概念一:
一般地,对于n个数x1,x2,…,xn,我们把
叫做这n个数的算术平均数,简称平均数. 记作:x,(读作:x拔)
x1 + x2 + … + xn
n
什么叫平均数
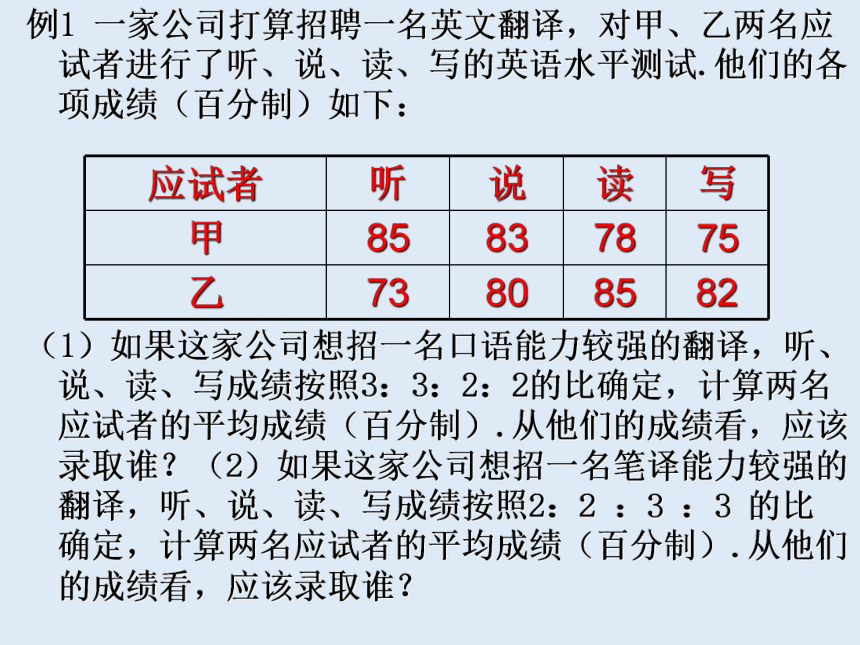
概念二:
一般地,若n个数x1,x2,…,xn的权分别是w1,w2,…,wn ,我们把
叫做这n个数的加权平均数.
加权平均数也是算术平均数哦!
数与该数的权的积之和
权之和
数据的权的意义
数据的权能够反映数据的相对“重要程度”.
归纳小结
例1 一家公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试.他们的各项成绩(百分制)如下:
(1)如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照3:3:2:2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?(2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2:2 :3 :3 的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
(1)如果这家公司想招一名口语能力较强的翻译,听说、读、写成绩按照3:3:2:2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
解:听说读写成绩按照3:3:2:2的比确定,
则甲的成绩为
乙的成绩为
显然甲的成绩比乙高,所以从成绩看,应该录取甲.
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
(2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2:2:3:3的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
解:听说读写成绩按照2:2:3:3的比确定,
则甲的成绩为
乙的成绩为
显然乙的成绩比甲高,所以从成绩看,应该录取乙.
加权平均数的意义
在一组数据中,由于每个数据的权不同,所以计算平均数时,用加权平均数,才符合实际.
归纳小结
由于各村种植的大户数不同,各村的户均种植面积对这三个村总的户均种植面积的影响不同,因此这三个村总的户均种植面积不能是三个村户均种植面积的算术平均数 ,而应该是加权平均数,即:
1.5×15表示白水村的大户百合种植面积吗?你能说出这个式子中分子,分母各表示什么吗?
数据的权不仅反映一组数据中各数据的个数,还能反映数据的相对“重要程度”.
村名 户数 户均种植面积(公顷)
白水村 15 1.5
文义村 7 2.1
永新村 10 1.8
这三个村的大户的户均种植面积是多少 (精确到0.1公顷)
例2.白水的百合今年又大面积种植,其中有三个村就有不少的种植大户,种植大户数和各村大户的户均栽种面积如下表:
权的常见形式:
3、百分比形式.如 50%、40% 、10%.
2、比的形式.如 3:3:2:2.
1、数据出现的次数形式.如 50、45、55.
例3.为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表:
这天5路公共汽车平均每班的载客量是多少
载客量/人 组中值 频数(班次)
1≤x<21 11 3
21≤x<41 31 5
41≤x<61 51 20
61≤x<81 71 22
81≤x<101 91 18
x<121 111 15
解:这天5路公共汽车平均每班的载客量是:
接下来,同学们请来思考这样的问题:
从上表中,你能知道这…天5路公共汽车大约有多少
班次的载客量在平均载客量以上吗 占全天总班次的
百分比是多少
种菜能手李大叔种植了一批新品种黄瓜.为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到下面的条形图.请估计这个新品种黄瓜.平均每株结多少根黄瓜.
练习
即样本平均数是13.因此,
可以估计这个新品种黄瓜的平均每株结13根黄瓜.
问:李大叔能不能用全面调查的方法去考察这个新品
种黄瓜的平均每株结的黄瓜根数呢
解:根据条形统计图,可知10的权是10,13的权是
15,14的权是20,15的权是18,所以
若n个数
的权分别是
则:
叫做这n个数的加权平均数.
数据的权能够反映的数据的相对“重要程度”.
加
权
平
均
数
认真体会加权平均数 权 的意义.
课堂小结
目标检测
1.若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是( )
A:(x+y)/2 B:(mx+ny)/(m+n)
C:(x+y)/(m+n) D:(mx+ny)/(x+y)
B
2.某次考试,5名学生的平均分是82,除甲外,其余4名学生的平均分是80,那么甲的得分是( )
(A)84 (B) 86
(C) 88 (D) 90
D
目标检测
3、万载三中规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末成绩占50%.小桐的三项成绩(百分制)依次是95分、90分、85分,小桐这学期的体育成绩是多少?
解:
目标检测
4.一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方
面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲
能力占40% 、演讲效果占10%的比例,计算选手的综合成绩(百分制).
进入决赛的前两名选手的单项成绩
如右表所示:
95
85
95
B
95
95
85
A
演讲效果
演讲能力
演讲内容
选手
请决出两人的名次.
解:选手A的最后得分是:
选手B的最后得分是:
所以选手B获得第一名,选手A获得第二名.
目标检测
通过本课学习,你收获了什么?
温故知新:
数据2、3、4、1、2的
平均数是________,这个
平均数叫做_________平
均数.
2.4
算术
20.1.1 平均数
第1课时 加权平均数
人教版八年级数学 下册
学习目标:
1.理解加权平均数的意义;
2.会用加权平均数分析一组数据的集中趋势,发展数据分析能力。
一次数学测验,3名同学的数学成绩分别是60,80和100分,则他们的平均成绩是多少?你怎样列式计算?算式中的分子分母分别表示什么含义?
平均数是一组数据的数值的代表值,它刻画了这组数据整体的平均状态.
如果有n个数(用χ1、χ2、χ3、…χn)那么它们的平均数我们表示为
80
x1 + x2 +… + xn
n
x =
x =
探究问题
如果知道有一个小组中3名学生得了60分,5名学生得了80分,还有一名学生得了100分,此时这个小组的数学测验平均分还是一问中的答案吗?该如何计算呢?
≈75.6
日常生活中,我们常用平均数表示一组数据的“平均水平”
概念一:
一般地,对于n个数x1,x2,…,xn,我们把
叫做这n个数的算术平均数,简称平均数. 记作:x,(读作:x拔)
x1 + x2 + … + xn
n
什么叫平均数
概念二:
一般地,若n个数x1,x2,…,xn的权分别是w1,w2,…,wn ,我们把
叫做这n个数的加权平均数.
加权平均数也是算术平均数哦!
数与该数的权的积之和
权之和
数据的权的意义
数据的权能够反映数据的相对“重要程度”.
归纳小结
例1 一家公司打算招聘一名英文翻译,对甲、乙两名应试者进行了听、说、读、写的英语水平测试.他们的各项成绩(百分制)如下:
(1)如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照3:3:2:2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?(2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2:2 :3 :3 的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
(1)如果这家公司想招一名口语能力较强的翻译,听说、读、写成绩按照3:3:2:2的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
解:听说读写成绩按照3:3:2:2的比确定,
则甲的成绩为
乙的成绩为
显然甲的成绩比乙高,所以从成绩看,应该录取甲.
应试者 听 说 读 写
甲 85 83 78 75
乙 73 80 85 82
(2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2:2:3:3的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁?
解:听说读写成绩按照2:2:3:3的比确定,
则甲的成绩为
乙的成绩为
显然乙的成绩比甲高,所以从成绩看,应该录取乙.
加权平均数的意义
在一组数据中,由于每个数据的权不同,所以计算平均数时,用加权平均数,才符合实际.
归纳小结
由于各村种植的大户数不同,各村的户均种植面积对这三个村总的户均种植面积的影响不同,因此这三个村总的户均种植面积不能是三个村户均种植面积的算术平均数 ,而应该是加权平均数,即:
1.5×15表示白水村的大户百合种植面积吗?你能说出这个式子中分子,分母各表示什么吗?
数据的权不仅反映一组数据中各数据的个数,还能反映数据的相对“重要程度”.
村名 户数 户均种植面积(公顷)
白水村 15 1.5
文义村 7 2.1
永新村 10 1.8
这三个村的大户的户均种植面积是多少 (精确到0.1公顷)
例2.白水的百合今年又大面积种植,其中有三个村就有不少的种植大户,种植大户数和各村大户的户均栽种面积如下表:
权的常见形式:
3、百分比形式.如 50%、40% 、10%.
2、比的形式.如 3:3:2:2.
1、数据出现的次数形式.如 50、45、55.
例3.为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表:
这天5路公共汽车平均每班的载客量是多少
载客量/人 组中值 频数(班次)
1≤x<21 11 3
21≤x<41 31 5
41≤x<61 51 20
61≤x<81 71 22
81≤x<101 91 18
x<121 111 15
解:这天5路公共汽车平均每班的载客量是:
接下来,同学们请来思考这样的问题:
从上表中,你能知道这…天5路公共汽车大约有多少
班次的载客量在平均载客量以上吗 占全天总班次的
百分比是多少
种菜能手李大叔种植了一批新品种黄瓜.为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到下面的条形图.请估计这个新品种黄瓜.平均每株结多少根黄瓜.
练习
即样本平均数是13.因此,
可以估计这个新品种黄瓜的平均每株结13根黄瓜.
问:李大叔能不能用全面调查的方法去考察这个新品
种黄瓜的平均每株结的黄瓜根数呢
解:根据条形统计图,可知10的权是10,13的权是
15,14的权是20,15的权是18,所以
若n个数
的权分别是
则:
叫做这n个数的加权平均数.
数据的权能够反映的数据的相对“重要程度”.
加
权
平
均
数
认真体会加权平均数 权 的意义.
课堂小结
目标检测
1.若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是( )
A:(x+y)/2 B:(mx+ny)/(m+n)
C:(x+y)/(m+n) D:(mx+ny)/(x+y)
B
2.某次考试,5名学生的平均分是82,除甲外,其余4名学生的平均分是80,那么甲的得分是( )
(A)84 (B) 86
(C) 88 (D) 90
D
目标检测
3、万载三中规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末成绩占50%.小桐的三项成绩(百分制)依次是95分、90分、85分,小桐这学期的体育成绩是多少?
解:
目标检测
4.一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方
面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲
能力占40% 、演讲效果占10%的比例,计算选手的综合成绩(百分制).
进入决赛的前两名选手的单项成绩
如右表所示:
95
85
95
B
95
95
85
A
演讲效果
演讲能力
演讲内容
选手
请决出两人的名次.
解:选手A的最后得分是:
选手B的最后得分是:
所以选手B获得第一名,选手A获得第二名.
目标检测
通过本课学习,你收获了什么?
