数学高中苏教版必修二1.2《点、线、面之间的位置关系--平面的基本性质》课件2
文档属性
| 名称 | 数学高中苏教版必修二1.2《点、线、面之间的位置关系--平面的基本性质》课件2 |  | |
| 格式 | zip | ||
| 文件大小 | 175.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-17 14:07:15 | ||
图片预览







文档简介
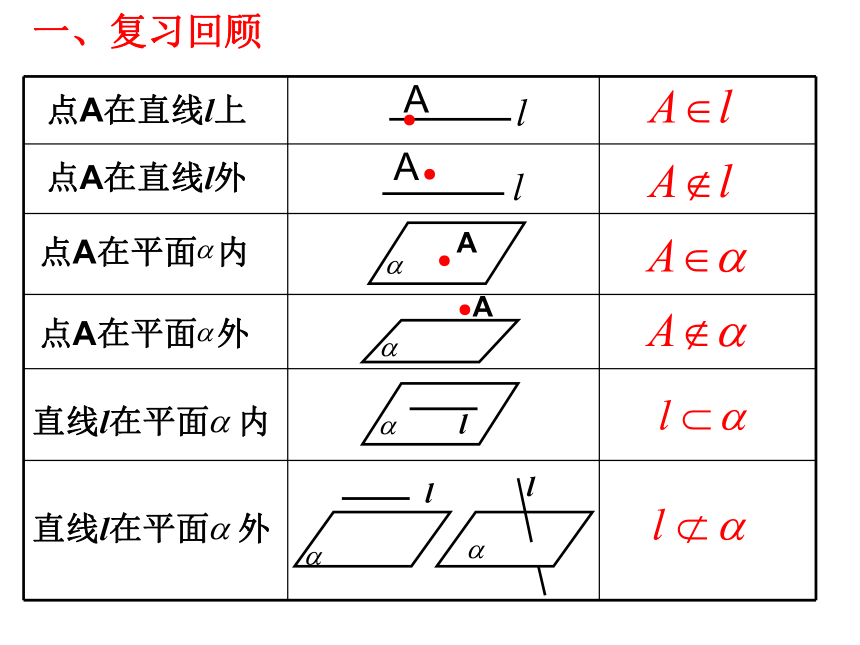
课件26张PPT。平面的基本性质(2)一、复习回顾点A在直线l上点A在直线l外公理3:经过不在同一条直线上的三点,有且只有一个平面.3、平面的基本性质的三种语言描述:公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.公理2:如果两个平面有一个公共点,那么它们还有其他公共点,这些公共点的集合是经过这个公共点的一条直线.符号语言:符号语言:符号语言:DC④二、建构数学推论1:经过一条直线和这条直线外的一点有
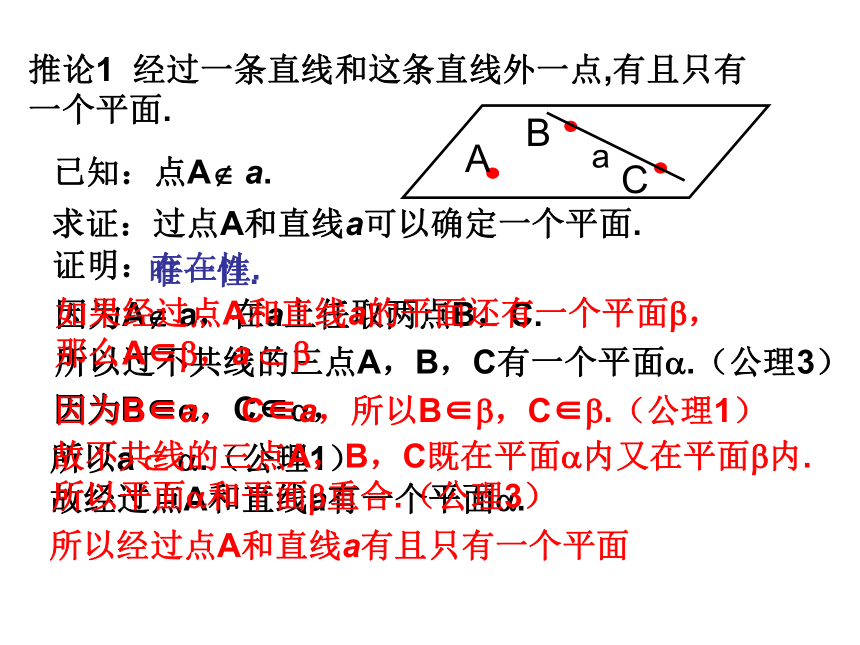
且只有一个平面.图形语言:符号语言:推论1 ?经过一条直线和这条直线外一点,有且只有
一个平面.已知:点A? a.求证:过点A和直线a可以确定一个平面.证明:存在性.因为A? a,在a上任取两点B,C.所以过不共线的三点A,B,C有一个平面?.(公理3)因为B∈?,C∈?,所以a ? ?.(公理1)故经过点A和直线a有一个平面?.唯一性.如果经过点A和直线a的平面还有一个平面?,
那么A∈?,a ? ?因为B∈a, C∈a,所以B∈?,C∈?.(公理1)故不共线的三点A,B,C既在平面?内又在平面?内.
所以平面?和平面?重合.(公理3)所以经过点A和直线a有且只有一个平面 证明:同理:即直线AD、BD、CD共面.推论2:经过两条相交直线,有且只有一个
平面.图形语言:符号语言:推论2:经过两条相交直线有且只有一个平面.证明:在a上取不同于点P的点A即:过 a,b 有一个平面.存在性:唯一性:平面的基本性质例2、两两相交且不同点的三条直线必在同一个平面内已知:AB∩AC=A,AB∩BC=B,AC∩BC=C求证:直线AB,BC,AC共面.证法一:因为AB∩AB=A所以直线AB,AC确定一个平面?.(推论2)因为B∈AB,C∈AC,所以B∈?,C∈?,故BC??.(公理1)因此直线AB,BC,CA共面.平面的基本性质
证法二:因为A? 直线BC上,所以过点A和直线BC确定平面?.(推论1)因为A∈?, B∈BC,所以B∈?.故AB ? ?,同理AC ? ?,所以AB,AC,BC共面.平面的基本性质
证法三:因为A,B,C三点不在一条直线上,所以过A,B,C三点可以确定平面?.(公理3)因为A∈?,B∈?,所以AB ? ?.(公理1)同理BC ? ?,AC ? ?,所以AB,BC,CA三直线共面.要证各线共面,先确定一个平面,再证明其他直线也在这个平面内。【例2】已知a,b,c,d是两两相交且不共点
的四条直线,求证:a,b,c,d共面.证明:如图(1)当Q、S、R、三点重合时,如图(2)同理:推论3:经过两条平行的直线有且只有一个
平面.图形语言:符号语言:推论3:经过两条平行的直线有且只有一个平面.证明:由平行线的定义知a,b在同一平面内设点A为直线a上任一点则点A在直线b外 又由推论1,过点A和直线b的平面只有一个A如果经过直线a , b的平面还有一个平面?,
那么a ∈?, b ? ?【例3】已知空间四点A、B、C、D不在同一平
面内,求证:AB、CD既不平行也不相
交.证明:与A、B、C、D不共面矛盾数学运用 画出由A1,C1,P三点所确定的平面α与长方体表面所在平面的交线。数学运用 6.如图,在棱长为a的正方体ABCD—A1B1C1D1中,
M、N分别是AA1、D1C1的中点,过D、M、N三点
的平面与正方体的下底面相交于直线l,(1)画出l的位置;
(2)设l∩A1B1=P,求PB1的长. 有三位同学证明如下,请判断正误:问题
研讨正方体中,试画出过其中三条棱的中点P,Q,R的平面截得正方体的截面形状.思考×√××√BD1B151或4或6∈∈1.平面的基本性质的三个推论.2.三个推论的应用.再见!
且只有一个平面.图形语言:符号语言:推论1 ?经过一条直线和这条直线外一点,有且只有
一个平面.已知:点A? a.求证:过点A和直线a可以确定一个平面.证明:存在性.因为A? a,在a上任取两点B,C.所以过不共线的三点A,B,C有一个平面?.(公理3)因为B∈?,C∈?,所以a ? ?.(公理1)故经过点A和直线a有一个平面?.唯一性.如果经过点A和直线a的平面还有一个平面?,
那么A∈?,a ? ?因为B∈a, C∈a,所以B∈?,C∈?.(公理1)故不共线的三点A,B,C既在平面?内又在平面?内.
所以平面?和平面?重合.(公理3)所以经过点A和直线a有且只有一个平面 证明:同理:即直线AD、BD、CD共面.推论2:经过两条相交直线,有且只有一个
平面.图形语言:符号语言:推论2:经过两条相交直线有且只有一个平面.证明:在a上取不同于点P的点A即:过 a,b 有一个平面.存在性:唯一性:平面的基本性质例2、两两相交且不同点的三条直线必在同一个平面内已知:AB∩AC=A,AB∩BC=B,AC∩BC=C求证:直线AB,BC,AC共面.证法一:因为AB∩AB=A所以直线AB,AC确定一个平面?.(推论2)因为B∈AB,C∈AC,所以B∈?,C∈?,故BC??.(公理1)因此直线AB,BC,CA共面.平面的基本性质
证法二:因为A? 直线BC上,所以过点A和直线BC确定平面?.(推论1)因为A∈?, B∈BC,所以B∈?.故AB ? ?,同理AC ? ?,所以AB,AC,BC共面.平面的基本性质
证法三:因为A,B,C三点不在一条直线上,所以过A,B,C三点可以确定平面?.(公理3)因为A∈?,B∈?,所以AB ? ?.(公理1)同理BC ? ?,AC ? ?,所以AB,BC,CA三直线共面.要证各线共面,先确定一个平面,再证明其他直线也在这个平面内。【例2】已知a,b,c,d是两两相交且不共点
的四条直线,求证:a,b,c,d共面.证明:如图(1)当Q、S、R、三点重合时,如图(2)同理:推论3:经过两条平行的直线有且只有一个
平面.图形语言:符号语言:推论3:经过两条平行的直线有且只有一个平面.证明:由平行线的定义知a,b在同一平面内设点A为直线a上任一点则点A在直线b外 又由推论1,过点A和直线b的平面只有一个A如果经过直线a , b的平面还有一个平面?,
那么a ∈?, b ? ?【例3】已知空间四点A、B、C、D不在同一平
面内,求证:AB、CD既不平行也不相
交.证明:与A、B、C、D不共面矛盾数学运用 画出由A1,C1,P三点所确定的平面α与长方体表面所在平面的交线。数学运用 6.如图,在棱长为a的正方体ABCD—A1B1C1D1中,
M、N分别是AA1、D1C1的中点,过D、M、N三点
的平面与正方体的下底面相交于直线l,(1)画出l的位置;
(2)设l∩A1B1=P,求PB1的长. 有三位同学证明如下,请判断正误:问题
研讨正方体中,试画出过其中三条棱的中点P,Q,R的平面截得正方体的截面形状.思考×√××√BD1B151或4或6∈∈1.平面的基本性质的三个推论.2.三个推论的应用.再见!
