4.2.1 等差数列的性质及应用(共29张PPT)
文档属性
| 名称 | 4.2.1 等差数列的性质及应用(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 20:42:15 | ||
图片预览








文档简介
(共29张PPT)
等差数列的性质及应用
1.理解等差数列、等差中项的概念,会用定义判定一个数
列是否是等差数列;(重点)
2.进一步加深对等差数列通项公式的理解、认识和应用;(难点)
3.掌握等差数列的有关性质.
例1.某公司购置了一台价值为220万元的设备,随着设备在使用过程中老化,其价值会逐年减少.经验表明,每经过一年其价值就会减少d(d为正常数)万元。已知这台设备的使用年限为10年,超过10年,它的价值将低于购进价值的5%,设备将报废.请确定d的取值范围.
分析:这台设备使用n年后的价值构成一个数列{an}。由题意可知,10年之内(含10年),这台设备的价值应不小于(220×5%=)11万元;而10年后,这台设备的价值应小于11万元。可以利用{an}的通项公式列不等式求解。
例1.某公司购置了一台价值为220万元的设备,随着设备在使用过程中老化,其价值会逐年减少.经验表明,每经过一年其价值就会减少d(d为正常数)万元。已知这台设备的使用年限为10年,超过10年,它的价值将低于购进价值的5%,设备将报废.请确定d的取值范围.
在通项公式中令n=1,得a1=p+q,
所以这个等差数列的首项是p+q,公差是p,
等差数列的性质(一)
an=3n+5
a1=8,d=3
1
3
4
14
118
2
17
an=12-2n
a1=10,d=-2
1
3
4
8
4
6
2
10
y=3x+5
y=12-2x
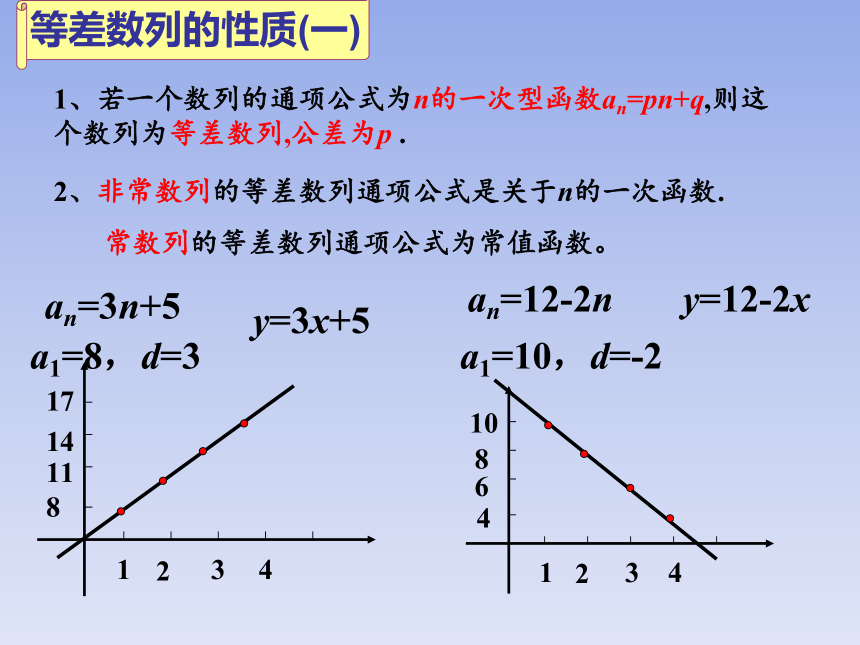
等差数列的性质(一)
1、若一个数列的通项公式为n的一次型函数an=pn+q,则这个数列为等差数列,公差为p .
2、非常数列的等差数列通项公式是关于n的一次函数.
常数列的等差数列通项公式为常值函数。
在一个数列中,从第2项起,每一项(有穷数列的末项除外)都是它前一项与后一项的等差中项.
如果a,A,b成等差数列,那么A叫a与b的等差中项.
如:数列:1,3,5,7,9,11,13,…中,
即:
等差数列的性质(二)
思考题:已知三个数成等差数列,和是12,积是48,求这三个数.
设数技巧
已知三个数成等差 数列,且和为已知时常利用对称性设三数为:a-d , a ,a+d
四个数怎么设?
(1)若有三个数成等差数列,则一般设为a-d,a,a+d;
(2)若有四个数成等差数列,则一般设为a-3d,a-d,a+d,a+3d;
(3)若有五个数成等差数列,则一般设为a-2d,a-d,a,a+d,a+2d.
等差数列的设法及求解
如何判断一个数列为等差数列
答:成立
等差数列的性质(三)
可推广到三项,四项等
注意:等式两边作和的项数必须一样多
例3是等差数列的一条性质,图4.2-2是它的一种情形。你能从几何角度解释等差数列的这一性质吗?
思考:
例4 在等差数列{an}中,
(1)已知 a6+a9+a12+a15=20,求a1+a20.
(2)已知a3+a11=10,求a6+a7+a8.
解:由a1+a20 =a6+a15=a9+a12 及a6+a9+a12+a15=20,可得a1+a20=10.
解:a3+a11 =a6+a8 =2a7 ,又a3+a11=10,
∴ a6+a7+a8= (a3+a11)=15.
熟记性质
(3)已知 a4+a5+a6+a7=56,a4a7=187,求a14及公差d.
解:a4+a5+a6+a7=56,∴a4+a7=28,①
又a4a7=187②, 联立①②解得
a4=17,
a7=11,
a4=11,
a7=17,
或
∴d= -2或2, 从而a14= -3或31.
例5.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2)b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
分析:(1){an}是一个确定的数列,只要把a1,a2表示为{bn}中的项,就可以利用等差数列的定义得出{bn}的通项公式;(2)设{an}中的第n项是{bn}中的第cn项,根据条件可以求出n与cn的关系式,由此即可判断b29是否为{an}的项。
例5.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2)b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
(2)数列{an}的各项依次是数列{bn}的第1,5,9,13,…项,这些下标构成一个首项为1,公差为4的等差数列{cn},则cn =4n-3.
令4n-3=29,解得n=8.
所以, b29是数列{an}的第8项.
思考:
(1)将前m项去掉,其余各项组成的数列是等差数列吗?如果是,他的首项与公差分别是多少?
am+1,am+2,…,an是等差数列
首项为am+1,公差为d,项数为n-m
等差数列的性质(四)
(2)取出数列中的所有奇数项,组成一个数列,是等差数列吗?如果是,他的首项与公差分别是多少?
a1,a3,a5,…是等差数列,首项为a1,公差为2d.
取出的是所有偶数项呢?
a2,a4,a6,…是等差数列,首项为a2,公差为2d.
等差数列的性质(四)
(3)取出数列中所有项是7的倍数的各项,组成一个数列,是等差数列吗?如果是,他的首项与公差是多少?
a7,a14,a21,…是等差数列,首项为a7,公差为7d.
取出的是所有k倍数的项呢?
ak,a2k,a3k,…是等差数列,首项为ak,公差为kd.
(4)数列a1+a2,a3+a4,a5+a6,……是等差数列吗?公差是多少?
是等差数列,公差为4d.
1、若数列{an}为等差数列,公差为d,则{can}也为等差数列,公差为 ____ 。
3、若数列{an}与{bn}分别是公差为d1、d2等差数列,则{an+bn}也为等差数列,{an-bn}也为等差数列,{pan+qbn}也为等差数列.
cd
2、若数列{an}为等差数列,公差为d, {c+an}(c为任一常数)是公差为__的等差数列;
d
等差数列的性质(四)
例题分析
重点题型:证明一个数列是等差数列
例题分析
重点题型:证明一个数列是等差数列
1.等差数列{an}的前三项依次为a-6,2a-5,-3a+2,则
a等于( )
A. -1 B. 1 C.-2 D. 2
B
2(2a-5)=(-3a+2) +(a-6).
提示:
2. (2012 福建高考)等差数列{an}中,
则数列{an}的公差为( )
A.1 B.2 C.3 D.4
B
提示:
3. 在等差数列{an}中,
(1)若a59=70,a80=112,求a101;
(2)若ap= q,aq= p ( p≠q ),求ap+q.
(一)等差数列的基本性质
1.在等差数列{an}中,若m+n=p+q,则am+an=ap+aq.(m,n,p,q∈N*)
2.等差中项:如果a,A,b成等差数列,那么A叫做
a与b的等差中项.
3.等差数列中项数成等差数列的项构成等差数列.
4.两个等差数列{an},{bn}的和、差还是等差数列,即{an±bn}也是等差数列,{pan}、{an+c}也是等差数列.
(二)等差数列的证明
1.利用定义;
2.利用等差中项的性质;
3.利用通项公式是一次函数的性质.
要追求真理,认识真理,更要依赖真理,这是人性中的最高品德。 ——培根
Thank you for watching !
等差数列的性质及应用
1.理解等差数列、等差中项的概念,会用定义判定一个数
列是否是等差数列;(重点)
2.进一步加深对等差数列通项公式的理解、认识和应用;(难点)
3.掌握等差数列的有关性质.
例1.某公司购置了一台价值为220万元的设备,随着设备在使用过程中老化,其价值会逐年减少.经验表明,每经过一年其价值就会减少d(d为正常数)万元。已知这台设备的使用年限为10年,超过10年,它的价值将低于购进价值的5%,设备将报废.请确定d的取值范围.
分析:这台设备使用n年后的价值构成一个数列{an}。由题意可知,10年之内(含10年),这台设备的价值应不小于(220×5%=)11万元;而10年后,这台设备的价值应小于11万元。可以利用{an}的通项公式列不等式求解。
例1.某公司购置了一台价值为220万元的设备,随着设备在使用过程中老化,其价值会逐年减少.经验表明,每经过一年其价值就会减少d(d为正常数)万元。已知这台设备的使用年限为10年,超过10年,它的价值将低于购进价值的5%,设备将报废.请确定d的取值范围.
在通项公式中令n=1,得a1=p+q,
所以这个等差数列的首项是p+q,公差是p,
等差数列的性质(一)
an=3n+5
a1=8,d=3
1
3
4
14
118
2
17
an=12-2n
a1=10,d=-2
1
3
4
8
4
6
2
10
y=3x+5
y=12-2x
等差数列的性质(一)
1、若一个数列的通项公式为n的一次型函数an=pn+q,则这个数列为等差数列,公差为p .
2、非常数列的等差数列通项公式是关于n的一次函数.
常数列的等差数列通项公式为常值函数。
在一个数列中,从第2项起,每一项(有穷数列的末项除外)都是它前一项与后一项的等差中项.
如果a,A,b成等差数列,那么A叫a与b的等差中项.
如:数列:1,3,5,7,9,11,13,…中,
即:
等差数列的性质(二)
思考题:已知三个数成等差数列,和是12,积是48,求这三个数.
设数技巧
已知三个数成等差 数列,且和为已知时常利用对称性设三数为:a-d , a ,a+d
四个数怎么设?
(1)若有三个数成等差数列,则一般设为a-d,a,a+d;
(2)若有四个数成等差数列,则一般设为a-3d,a-d,a+d,a+3d;
(3)若有五个数成等差数列,则一般设为a-2d,a-d,a,a+d,a+2d.
等差数列的设法及求解
如何判断一个数列为等差数列
答:成立
等差数列的性质(三)
可推广到三项,四项等
注意:等式两边作和的项数必须一样多
例3是等差数列的一条性质,图4.2-2是它的一种情形。你能从几何角度解释等差数列的这一性质吗?
思考:
例4 在等差数列{an}中,
(1)已知 a6+a9+a12+a15=20,求a1+a20.
(2)已知a3+a11=10,求a6+a7+a8.
解:由a1+a20 =a6+a15=a9+a12 及a6+a9+a12+a15=20,可得a1+a20=10.
解:a3+a11 =a6+a8 =2a7 ,又a3+a11=10,
∴ a6+a7+a8= (a3+a11)=15.
熟记性质
(3)已知 a4+a5+a6+a7=56,a4a7=187,求a14及公差d.
解:a4+a5+a6+a7=56,∴a4+a7=28,①
又a4a7=187②, 联立①②解得
a4=17,
a7=11,
a4=11,
a7=17,
或
∴d= -2或2, 从而a14= -3或31.
例5.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2)b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
分析:(1){an}是一个确定的数列,只要把a1,a2表示为{bn}中的项,就可以利用等差数列的定义得出{bn}的通项公式;(2)设{an}中的第n项是{bn}中的第cn项,根据条件可以求出n与cn的关系式,由此即可判断b29是否为{an}的项。
例5.已知等差数列{an}的首项a1=2,公差d=8,在{an}中每相邻两项之间都插入3个数,使它们和原数列的数一起构成一个新的等差数列{bn}.
(1)求数列{bn}的通项公式.
(2)b29是不是数列{an}的项?若是,它是{an}的第几项?若不是,说明理由.
(2)数列{an}的各项依次是数列{bn}的第1,5,9,13,…项,这些下标构成一个首项为1,公差为4的等差数列{cn},则cn =4n-3.
令4n-3=29,解得n=8.
所以, b29是数列{an}的第8项.
思考:
(1)将前m项去掉,其余各项组成的数列是等差数列吗?如果是,他的首项与公差分别是多少?
am+1,am+2,…,an是等差数列
首项为am+1,公差为d,项数为n-m
等差数列的性质(四)
(2)取出数列中的所有奇数项,组成一个数列,是等差数列吗?如果是,他的首项与公差分别是多少?
a1,a3,a5,…是等差数列,首项为a1,公差为2d.
取出的是所有偶数项呢?
a2,a4,a6,…是等差数列,首项为a2,公差为2d.
等差数列的性质(四)
(3)取出数列中所有项是7的倍数的各项,组成一个数列,是等差数列吗?如果是,他的首项与公差是多少?
a7,a14,a21,…是等差数列,首项为a7,公差为7d.
取出的是所有k倍数的项呢?
ak,a2k,a3k,…是等差数列,首项为ak,公差为kd.
(4)数列a1+a2,a3+a4,a5+a6,……是等差数列吗?公差是多少?
是等差数列,公差为4d.
1、若数列{an}为等差数列,公差为d,则{can}也为等差数列,公差为 ____ 。
3、若数列{an}与{bn}分别是公差为d1、d2等差数列,则{an+bn}也为等差数列,{an-bn}也为等差数列,{pan+qbn}也为等差数列.
cd
2、若数列{an}为等差数列,公差为d, {c+an}(c为任一常数)是公差为__的等差数列;
d
等差数列的性质(四)
例题分析
重点题型:证明一个数列是等差数列
例题分析
重点题型:证明一个数列是等差数列
1.等差数列{an}的前三项依次为a-6,2a-5,-3a+2,则
a等于( )
A. -1 B. 1 C.-2 D. 2
B
2(2a-5)=(-3a+2) +(a-6).
提示:
2. (2012 福建高考)等差数列{an}中,
则数列{an}的公差为( )
A.1 B.2 C.3 D.4
B
提示:
3. 在等差数列{an}中,
(1)若a59=70,a80=112,求a101;
(2)若ap= q,aq= p ( p≠q ),求ap+q.
(一)等差数列的基本性质
1.在等差数列{an}中,若m+n=p+q,则am+an=ap+aq.(m,n,p,q∈N*)
2.等差中项:如果a,A,b成等差数列,那么A叫做
a与b的等差中项.
3.等差数列中项数成等差数列的项构成等差数列.
4.两个等差数列{an},{bn}的和、差还是等差数列,即{an±bn}也是等差数列,{pan}、{an+c}也是等差数列.
(二)等差数列的证明
1.利用定义;
2.利用等差中项的性质;
3.利用通项公式是一次函数的性质.
要追求真理,认识真理,更要依赖真理,这是人性中的最高品德。 ——培根
Thank you for watching !
