4.3.1 等比数列的概念(共27张PPT)
文档属性
| 名称 | 4.3.1 等比数列的概念(共27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
4.3.1 等比数列的概念
1.理解等比数列的概念;(重点)
2.掌握等比数列的通项公式,通过实例发现数列的等比关系,提高数学建模的能力.(重点、难点)
请看下面几个问题中的数列.
1.两河流域发掘的古巴比伦时期的泥版上记录了下面的数列:
古巴比伦人用60进制记数,这里转化为十进制.
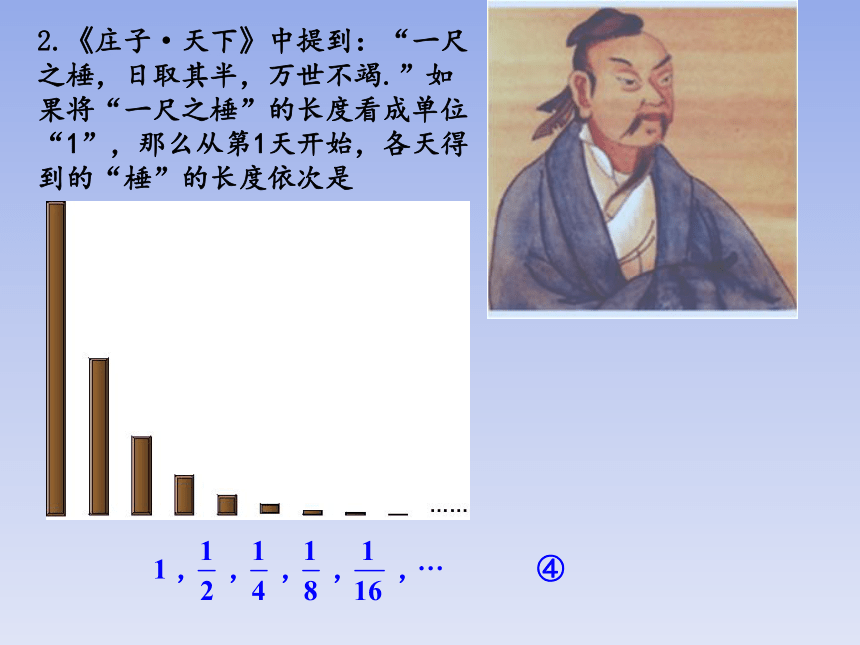
2.《庄子·天下》中提到:“一尺之棰,日取其半,万世不竭.”如果将“一尺之棰”的长度看成单位“1”,那么从第1天开始,各天得到的“棰”的长度依次是
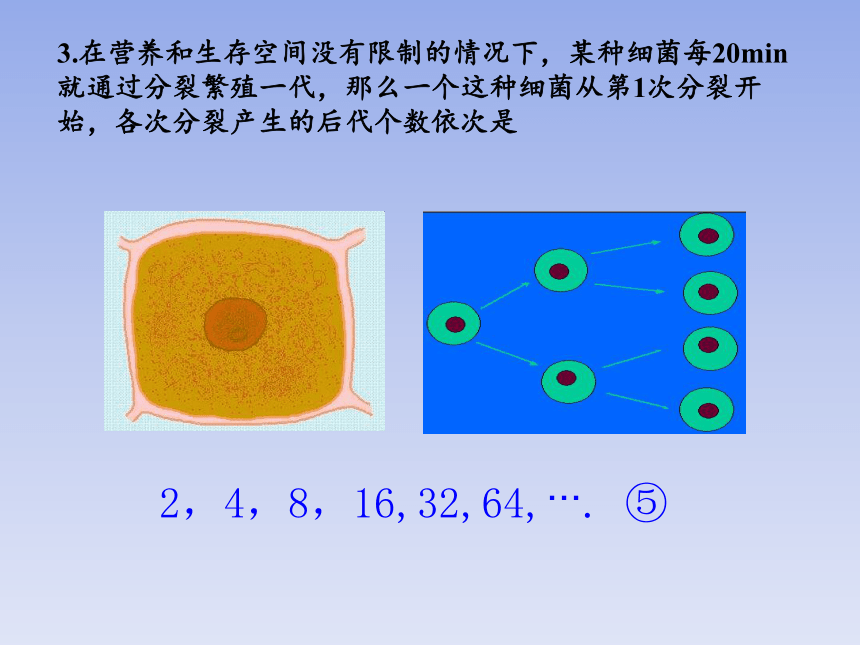
3.在营养和生存空间没有限制的情况下,某种细菌每20min就通过分裂繁殖一代,那么一个这种细菌从第1次分裂开始,各次分裂产生的后代个数依次是
2,4,8,16,32,64, . ⑤
4.某人存入银行a元,存期为5年,年利率为r,那么按照复利,他5年内每年末得到的本利和分别是
引入
举例
a(1+r), a(1+r) 2, a(1+r) 3, a(1+r) 4, a(1+r) 5. ⑥
复利是指把前一期的利息和本金加在一起算作本金,再计算下一期的利息.
类比等差数列的研究,你认为可以通过怎样的运算发现以上数列的取值规律?你发现了什么规律?
如果用{an}表示数列①,那么有
这表明,数列①有这样的取值规律:从第2项起,每一项与它的前一项的比都等于9.
其余几个数列也有这样的取值规律,请你写出相应的规律.
我们可以通过除法运算探究以上数列的取值规律.
2,4,8,16,32,64, . ⑤
a(1+r), a(1+r) 2, a(1+r) 3, a(1+r) 4, a(1+r) 5. ⑥
2.类比等差数列的概念,从上述几个数列的规律中,你能抽象出等比数列的概念吗?
思考
1.这几个数列的共同特征是什么?
从第二项起,每一项与它的前一项的比都等于同一个常数.
如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比,记为q(q≠0).
递推公式:
探究一:等比数列的定义
(q≠0)
为什么?
例如,数列①~⑥的公比依次是
思考:
(1)等差数列的项、公差均可以是0吗?等比数列呢?
(2)常数列是等差数列吗?是等比数列吗?
(3)是否存在既是等差数列又是等比数列的数列?
(4)q>0时,等比数列各项的符号有何特点?q<0时呢?
常数列是等差数列,公差为0;
非零常数列是等比数列,公比为1.
非零常数列既是等差数列又是等比数列,公差为0,公比为1.
q>0时,等比数列各项符号和首项a1保持一致;
q<0时,等比数列各项符号正负间隔,
奇数项和偶数项分别同号。
注意:
1.公比是等比数列从第2项起,每一项与它的前一项的比,不能颠倒.
2.对于一个给定的等比数列,它的公比是同一个常数.
巩固练:下列数列中能否确定是等比数列,若是,公比为多少?
① 1,-1,1,…,(-1)n+1 ;
②1,2,4,6…;
③
④ 2a,2a,2a,…,2a.
⑤已知a1=2,an=3an+1
√
√
√
×
×
非零的
常数列
q=-1
q=1
若a,G,b三个数成等比数列,那么这三个数有何恒等关系?
结论:G2=ab
G叫做a,b的等比中项
探究二、等比中项
练一练:
(1)4与9的等比中项是______
(2)-1,2,x,8,-16成等比数列,则x= ______
(1)只有同号两数才有等比中项
(2)两数的等比中项有2个
推导一:归纳法
探究三:通项公式
不完全归纳法
推导二:累乘法
两边分别相乘,可得:
累乘法
由等比数列的定义,有
等比数列的通项公式
在等比数列{an}中,若已知某一项为am,公比为q, 求该数列的任意项an.
等比数列通项公式的推广公式:
思考:等比数列的通项公式与我们学过的哪种函数有关系?
例1
例1
例2
等比数列的任意一项都可以由该数列的某一项和公比表示.
例3
1.判断下列数列是否是等比数列.如果是,写出它的公比.
2.已知{an}是一个公比为q的等比数列,在下表中填上适当的数.
3.在等比数列{an}中,a1a3=36,a2+a4=60.求a1和公比q.
1.理解并掌握等比数列的定义及数学表达式:
3.等比中项:有两个,
2.等比数列的通项公式:
累乘法
推导方法:
幸运所需要的美德是节制,而厄运所需要的美德是坚忍,后者比前者更为难能可贵。
——培根
Thank you for watching !
4.3.1 等比数列的概念
1.理解等比数列的概念;(重点)
2.掌握等比数列的通项公式,通过实例发现数列的等比关系,提高数学建模的能力.(重点、难点)
请看下面几个问题中的数列.
1.两河流域发掘的古巴比伦时期的泥版上记录了下面的数列:
古巴比伦人用60进制记数,这里转化为十进制.
2.《庄子·天下》中提到:“一尺之棰,日取其半,万世不竭.”如果将“一尺之棰”的长度看成单位“1”,那么从第1天开始,各天得到的“棰”的长度依次是
3.在营养和生存空间没有限制的情况下,某种细菌每20min就通过分裂繁殖一代,那么一个这种细菌从第1次分裂开始,各次分裂产生的后代个数依次是
2,4,8,16,32,64, . ⑤
4.某人存入银行a元,存期为5年,年利率为r,那么按照复利,他5年内每年末得到的本利和分别是
引入
举例
a(1+r), a(1+r) 2, a(1+r) 3, a(1+r) 4, a(1+r) 5. ⑥
复利是指把前一期的利息和本金加在一起算作本金,再计算下一期的利息.
类比等差数列的研究,你认为可以通过怎样的运算发现以上数列的取值规律?你发现了什么规律?
如果用{an}表示数列①,那么有
这表明,数列①有这样的取值规律:从第2项起,每一项与它的前一项的比都等于9.
其余几个数列也有这样的取值规律,请你写出相应的规律.
我们可以通过除法运算探究以上数列的取值规律.
2,4,8,16,32,64, . ⑤
a(1+r), a(1+r) 2, a(1+r) 3, a(1+r) 4, a(1+r) 5. ⑥
2.类比等差数列的概念,从上述几个数列的规律中,你能抽象出等比数列的概念吗?
思考
1.这几个数列的共同特征是什么?
从第二项起,每一项与它的前一项的比都等于同一个常数.
如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比,记为q(q≠0).
递推公式:
探究一:等比数列的定义
(q≠0)
为什么?
例如,数列①~⑥的公比依次是
思考:
(1)等差数列的项、公差均可以是0吗?等比数列呢?
(2)常数列是等差数列吗?是等比数列吗?
(3)是否存在既是等差数列又是等比数列的数列?
(4)q>0时,等比数列各项的符号有何特点?q<0时呢?
常数列是等差数列,公差为0;
非零常数列是等比数列,公比为1.
非零常数列既是等差数列又是等比数列,公差为0,公比为1.
q>0时,等比数列各项符号和首项a1保持一致;
q<0时,等比数列各项符号正负间隔,
奇数项和偶数项分别同号。
注意:
1.公比是等比数列从第2项起,每一项与它的前一项的比,不能颠倒.
2.对于一个给定的等比数列,它的公比是同一个常数.
巩固练:下列数列中能否确定是等比数列,若是,公比为多少?
① 1,-1,1,…,(-1)n+1 ;
②1,2,4,6…;
③
④ 2a,2a,2a,…,2a.
⑤已知a1=2,an=3an+1
√
√
√
×
×
非零的
常数列
q=-1
q=1
若a,G,b三个数成等比数列,那么这三个数有何恒等关系?
结论:G2=ab
G叫做a,b的等比中项
探究二、等比中项
练一练:
(1)4与9的等比中项是______
(2)-1,2,x,8,-16成等比数列,则x= ______
(1)只有同号两数才有等比中项
(2)两数的等比中项有2个
推导一:归纳法
探究三:通项公式
不完全归纳法
推导二:累乘法
两边分别相乘,可得:
累乘法
由等比数列的定义,有
等比数列的通项公式
在等比数列{an}中,若已知某一项为am,公比为q, 求该数列的任意项an.
等比数列通项公式的推广公式:
思考:等比数列的通项公式与我们学过的哪种函数有关系?
例1
例1
例2
等比数列的任意一项都可以由该数列的某一项和公比表示.
例3
1.判断下列数列是否是等比数列.如果是,写出它的公比.
2.已知{an}是一个公比为q的等比数列,在下表中填上适当的数.
3.在等比数列{an}中,a1a3=36,a2+a4=60.求a1和公比q.
1.理解并掌握等比数列的定义及数学表达式:
3.等比中项:有两个,
2.等比数列的通项公式:
累乘法
推导方法:
幸运所需要的美德是节制,而厄运所需要的美德是坚忍,后者比前者更为难能可贵。
——培根
Thank you for watching !
