4.3.1 等比数列的性质(共28张PPT)
文档属性
| 名称 | 4.3.1 等比数列的性质(共28张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 20:43:29 | ||
图片预览






文档简介
(共28张PPT)
4.3.1 等比数列的性质
1.理解并掌握等比数列的性质及其初步应用;
(重点、难点)
2.引导学生学习观察、类比、猜测等推理方法,提高学生分析、综合、抽象、概括等逻辑思维能力.
1.理解并掌握等比数列的定义及数学表达式:
3.等比中项:有两个,
2.等比数列的通项公式:
累乘法
推导方法:
(1) 1,2,4,8,16,…
观察数列
(3) 4,4,4,4,4,4,4,…
(4) 1,-1,1,-1,1,-1,1,…
公比 q=2
公比 q=1
公比 q=-1
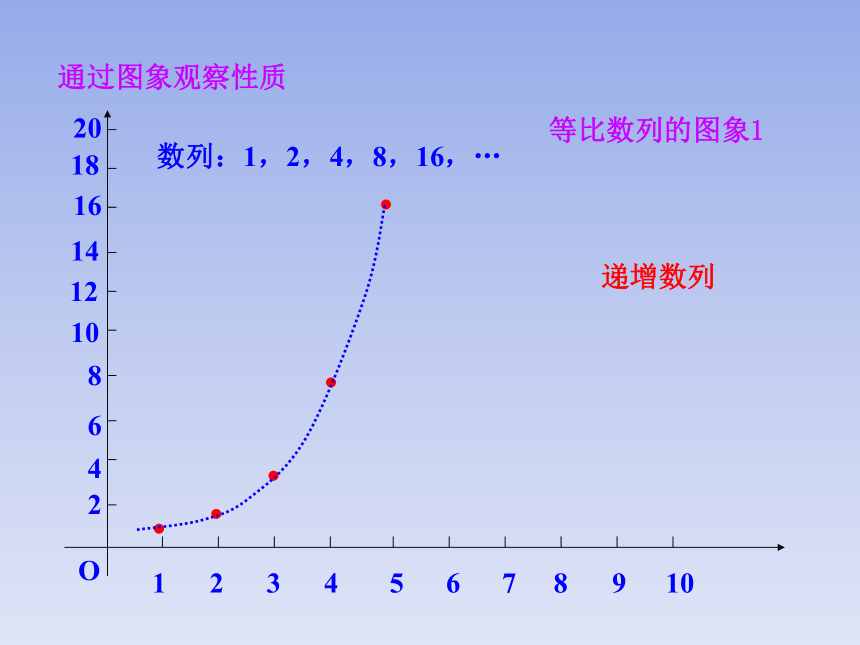
等比数列的图象1
数列:1,2,4,8,16,…
1
2
3
4
5
6
7
8
9
10
2
4
6
8
10
12
14
16
18
20
O
●
●
●
●
●
递增数列
通过图象观察性质
等比数列的图象2
1
2
3
4
5
6
7
8
9
10
O
数列:
●
●
●
●
●
●
●
1
2
3
4
5
6
7
8
9
10
递减数列
等比数列的图象3
1
2
3
4
5
6
7
8
9
10
2
4
6
8
10
12
14
16
18
20
O
数列:4,4,4,4,4,4,4,…
●
●
●
●
●
●
●
●
●
●
常数列
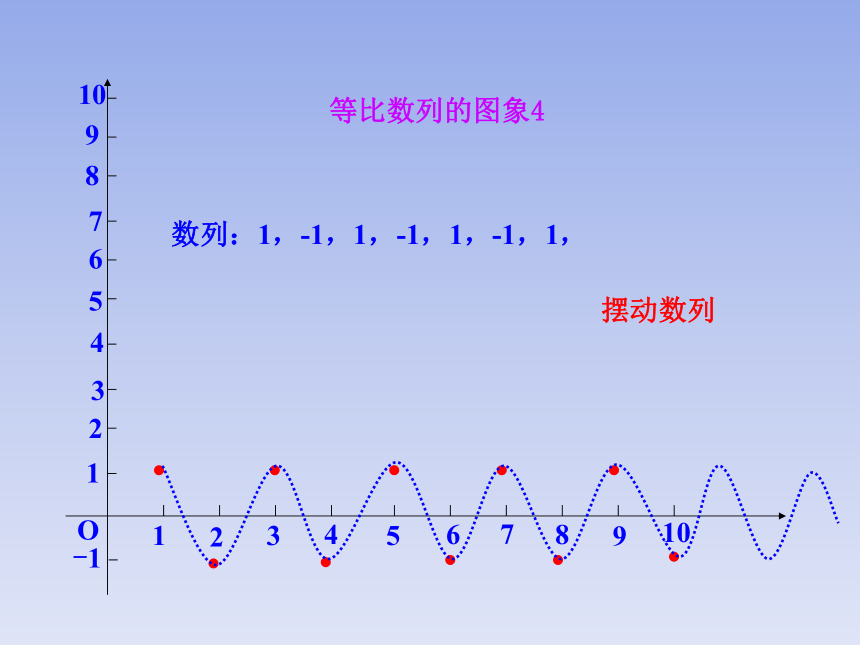
等比数列的图象4
1
2
3
4
5
6
7
8
9
10
O
1
2
3
4
5
6
7
8
9
10
●
●
●
●
●
●
●
●
●
●
数列:1,-1,1,-1,1,-1,1,
摆动数列
-1
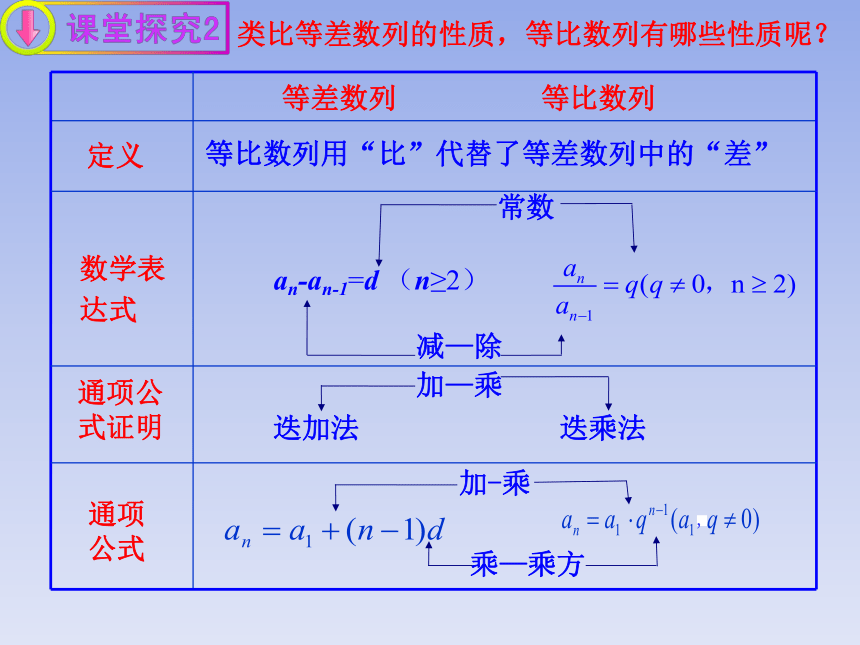
an-an-1=d (n≥2)
等差数列 等比数列
常数
减—除
加—乘
加-乘
乘—乘方
迭加法
迭乘法
等比数列用“比”代替了等差数列中的“差”
定义
数学表
达式
通项公式证明
通项 公式
,
类比等差数列的性质,等比数列有哪些性质呢?
由等差数列的性质,猜想等比数列的性质
{an}是公差为d的等差数列 {bn}是公比为q的等比数列
性质1: an=am+(n-m)d
性质2:若an-k,an,an+k
是{an}中的三项 ,
则2an=an+k+ an-k 猜想2:
性质3: 若n+m=p+q,
则am+an=ap+aq
猜想1:
若bn-k,bn,bn+k
是{bn}中的三项,则
猜想3:若n+m=p+q,则
性质4:从原数列中取出偶数项组成的新数列公差为2d.
(可推广)
性质5: 若{cn}是公差为d′的等差数列,则数列{an+cn}是公差为d+d′的等差数列.
猜想5:若{dn}是公比为q′的等比数列,则数列{bn · dn}是公比为q·q′的等比数列.
猜想4:从原数列中取出偶数项,组成的新数列公比为 (可推广)
若数列{an}是公比为q的等比数列,则
当q>1,a1>0或0当q>1, a1<0或00时, {an}是递减数列;
当q=1时, {an}是常数列;
当q<0时, {an}是摆动数列.
(2)an≠0,且anan+2>0.
(3)an=amqn-m(n,m∈N*).
(4)当n+m=p+q(n,m,p,q∈N*)时,有anam=apaq.
(5)当{an}是有穷数列时,与首末两项等距离的两项的积都相等,且等于首末两项的积.
(7)若{bn}是公比为q′的等比数列,则数列{anbn }是公比为qq′的等比数列.
(6)数列{λan}(λ为不等于零的常数)仍是公比为q的等比数列.
(9)在{an}中,每隔k(k∈N*)项取出一项,按原来顺序排
列,所得的新数列仍为等比数列,且公比为qk+1.
(10)当m,n,p(m,n,p∈N*)成等差数列时,am , an , ap 成等比数列.
例1
(1)若以月利率0.400%的复利计息,12个月能获得多少利息(精确到1元)?
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息(精确到10-5)?
分析:复利是指把前一期的利息与本金之和算作本金,再计算下一期的利息,所以若原始本金为a元,每期的利率为r,则从第一期开始,各期的本利和a,a(1+r) , a(1+r) 2,…构成等比数列.
例2
用10000元购买某个理财产品一年.
(1)若以月利率0.400%的复利计息,12个月能获得多少利息(精确到1元)?
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息(精确到10-5)?
例4
用10000元购买某个理财产品一年.
分析:根据题意,需要从等差数列、等比数列的定义出发,利用指数、对数的知识进行证明.
例3
例5
思考
某工厂去年12月试产1050个高新电子产品,产品合格率为90%.从今年1月开始,工厂在接下来的两年中将生产这款产品.1月按去年12月的产量和产品合格率生产,以后每月的产量都在前一个月的基础上提高5%,产品合格率比前一个月增加0.4%,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
例4
分析:设从今年1月起,各月的产量及不合格率分别构成数列{an},{bn},则各月不合格品的数量构成数列{anbn}.由题意可知,数列{an}是等比数列,{bn}是等差数列.由于数列{anbn}既非等差数列又非等比数列,所以可以先列表观察规律,再寻求问题的解决方法.
某工厂去年12月试产1050个高新电子产品,产品合格率为90%.从今年1月开始,工厂在接下来的两年中将生产这款产品.1月按去年12月的产量和产品合格率生产,以后每月的产量都在前一个月的基础上提高5%,产品合格率比前一个月增加0.4%,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
例4
由计算工具计算(精确到0.1),并列表(表4.3-1)
⒈在等比数列{an}中,a2=-2,a5=54,a8= .
⒉在等比数列{an}中,an>0,a2 a4+2a3a5+a4a6=36,
那么a3+a5= _ .
⒊在等比数列{an}中, a15 =10, a45=90,则
a30 =__________.
⒋在等比数列{an}中,a1+a2 =30, a3+a4 =120,
则a5+a6=_____.
-1 458
6
30
480
或-30
5.
的等比中项是___________.
6.如果三角形的三边成等比数列,则公比 q 的取值范
围是___________________.
7.已知正数等比数列
中,
8.设数列
是等比数列,且
则
对所有的自然数 n 都成立,则公比 q =___________.
证明或判断一个数列为等比数列的方法:
等比数列的性质:
1.an=amqn-m(n,m∈N*)
2.若m+n=p+q,则aman= apaq(m,n,p,q∈N*)
3.等比数列中,每隔k项取一项,按原来顺序排列,所得的新数列仍为等比数列.
4.a1a2, a3a4, a5a6, …仍为等比数列.
5.在等比数列中,从第二项起,每一项都是它等距离的前后两项的等比中项.
星星——只能白了青年人的发,不能灰了青年人的心。
——冰心
Thank you for watching !
4.3.1 等比数列的性质
1.理解并掌握等比数列的性质及其初步应用;
(重点、难点)
2.引导学生学习观察、类比、猜测等推理方法,提高学生分析、综合、抽象、概括等逻辑思维能力.
1.理解并掌握等比数列的定义及数学表达式:
3.等比中项:有两个,
2.等比数列的通项公式:
累乘法
推导方法:
(1) 1,2,4,8,16,…
观察数列
(3) 4,4,4,4,4,4,4,…
(4) 1,-1,1,-1,1,-1,1,…
公比 q=2
公比 q=1
公比 q=-1
等比数列的图象1
数列:1,2,4,8,16,…
1
2
3
4
5
6
7
8
9
10
2
4
6
8
10
12
14
16
18
20
O
●
●
●
●
●
递增数列
通过图象观察性质
等比数列的图象2
1
2
3
4
5
6
7
8
9
10
O
数列:
●
●
●
●
●
●
●
1
2
3
4
5
6
7
8
9
10
递减数列
等比数列的图象3
1
2
3
4
5
6
7
8
9
10
2
4
6
8
10
12
14
16
18
20
O
数列:4,4,4,4,4,4,4,…
●
●
●
●
●
●
●
●
●
●
常数列
等比数列的图象4
1
2
3
4
5
6
7
8
9
10
O
1
2
3
4
5
6
7
8
9
10
●
●
●
●
●
●
●
●
●
●
数列:1,-1,1,-1,1,-1,1,
摆动数列
-1
an-an-1=d (n≥2)
等差数列 等比数列
常数
减—除
加—乘
加-乘
乘—乘方
迭加法
迭乘法
等比数列用“比”代替了等差数列中的“差”
定义
数学表
达式
通项公式证明
通项 公式
,
类比等差数列的性质,等比数列有哪些性质呢?
由等差数列的性质,猜想等比数列的性质
{an}是公差为d的等差数列 {bn}是公比为q的等比数列
性质1: an=am+(n-m)d
性质2:若an-k,an,an+k
是{an}中的三项 ,
则2an=an+k+ an-k 猜想2:
性质3: 若n+m=p+q,
则am+an=ap+aq
猜想1:
若bn-k,bn,bn+k
是{bn}中的三项,则
猜想3:若n+m=p+q,则
性质4:从原数列中取出偶数项组成的新数列公差为2d.
(可推广)
性质5: 若{cn}是公差为d′的等差数列,则数列{an+cn}是公差为d+d′的等差数列.
猜想5:若{dn}是公比为q′的等比数列,则数列{bn · dn}是公比为q·q′的等比数列.
猜想4:从原数列中取出偶数项,组成的新数列公比为 (可推广)
若数列{an}是公比为q的等比数列,则
当q>1,a1>0或0
当q=1时, {an}是常数列;
当q<0时, {an}是摆动数列.
(2)an≠0,且anan+2>0.
(3)an=amqn-m(n,m∈N*).
(4)当n+m=p+q(n,m,p,q∈N*)时,有anam=apaq.
(5)当{an}是有穷数列时,与首末两项等距离的两项的积都相等,且等于首末两项的积.
(7)若{bn}是公比为q′的等比数列,则数列{anbn }是公比为qq′的等比数列.
(6)数列{λan}(λ为不等于零的常数)仍是公比为q的等比数列.
(9)在{an}中,每隔k(k∈N*)项取出一项,按原来顺序排
列,所得的新数列仍为等比数列,且公比为qk+1.
(10)当m,n,p(m,n,p∈N*)成等差数列时,am , an , ap 成等比数列.
例1
(1)若以月利率0.400%的复利计息,12个月能获得多少利息(精确到1元)?
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息(精确到10-5)?
分析:复利是指把前一期的利息与本金之和算作本金,再计算下一期的利息,所以若原始本金为a元,每期的利率为r,则从第一期开始,各期的本利和a,a(1+r) , a(1+r) 2,…构成等比数列.
例2
用10000元购买某个理财产品一年.
(1)若以月利率0.400%的复利计息,12个月能获得多少利息(精确到1元)?
(2)若以季度复利计息,存4个季度,则当每季度利率为多少时,按季结算的利息不少于按月结算的利息(精确到10-5)?
例4
用10000元购买某个理财产品一年.
分析:根据题意,需要从等差数列、等比数列的定义出发,利用指数、对数的知识进行证明.
例3
例5
思考
某工厂去年12月试产1050个高新电子产品,产品合格率为90%.从今年1月开始,工厂在接下来的两年中将生产这款产品.1月按去年12月的产量和产品合格率生产,以后每月的产量都在前一个月的基础上提高5%,产品合格率比前一个月增加0.4%,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
例4
分析:设从今年1月起,各月的产量及不合格率分别构成数列{an},{bn},则各月不合格品的数量构成数列{anbn}.由题意可知,数列{an}是等比数列,{bn}是等差数列.由于数列{anbn}既非等差数列又非等比数列,所以可以先列表观察规律,再寻求问题的解决方法.
某工厂去年12月试产1050个高新电子产品,产品合格率为90%.从今年1月开始,工厂在接下来的两年中将生产这款产品.1月按去年12月的产量和产品合格率生产,以后每月的产量都在前一个月的基础上提高5%,产品合格率比前一个月增加0.4%,那么生产该产品一年后,月不合格品的数量能否控制在100个以内?
例4
由计算工具计算(精确到0.1),并列表(表4.3-1)
⒈在等比数列{an}中,a2=-2,a5=54,a8= .
⒉在等比数列{an}中,an>0,a2 a4+2a3a5+a4a6=36,
那么a3+a5= _ .
⒊在等比数列{an}中, a15 =10, a45=90,则
a30 =__________.
⒋在等比数列{an}中,a1+a2 =30, a3+a4 =120,
则a5+a6=_____.
-1 458
6
30
480
或-30
5.
的等比中项是___________.
6.如果三角形的三边成等比数列,则公比 q 的取值范
围是___________________.
7.已知正数等比数列
中,
8.设数列
是等比数列,且
则
对所有的自然数 n 都成立,则公比 q =___________.
证明或判断一个数列为等比数列的方法:
等比数列的性质:
1.an=amqn-m(n,m∈N*)
2.若m+n=p+q,则aman= apaq(m,n,p,q∈N*)
3.等比数列中,每隔k项取一项,按原来顺序排列,所得的新数列仍为等比数列.
4.a1a2, a3a4, a5a6, …仍为等比数列.
5.在等比数列中,从第二项起,每一项都是它等距离的前后两项的等比中项.
星星——只能白了青年人的发,不能灰了青年人的心。
——冰心
Thank you for watching !
