4.2等差数列(一)(共25张PPT)
文档属性
| 名称 | 4.2等差数列(一)(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 20:52:43 | ||
图片预览







文档简介
(共25张PPT)
2.2等差数列(一)
复习回顾:
1.数列定义:按照一定顺序排成的一列数,
简记作:{an}
2.通项公式:数列{an}中第n项an与n之间的关系式
3.数列的分类
(1)按项数分:
有穷数列,
(2)按项之间的大小关系:
递增数列,
递减数列,
无穷数列
摆动数列,
常数列。
4.数列的实质
5.递推公式:
如果已知{an}的第1项(或前n项),且任一项an与它的前一项an-1(或前n项)间的关系可用一个公式来表示,这个公式叫做数列的递推公式.
在过去的三百多年里,人们分别在下列时间里观测到了哈雷慧星:
(1)1682,1758,1834,1910,1986,( )
你能预测出下一次的大致时间吗?
2062
相差76
引入新课
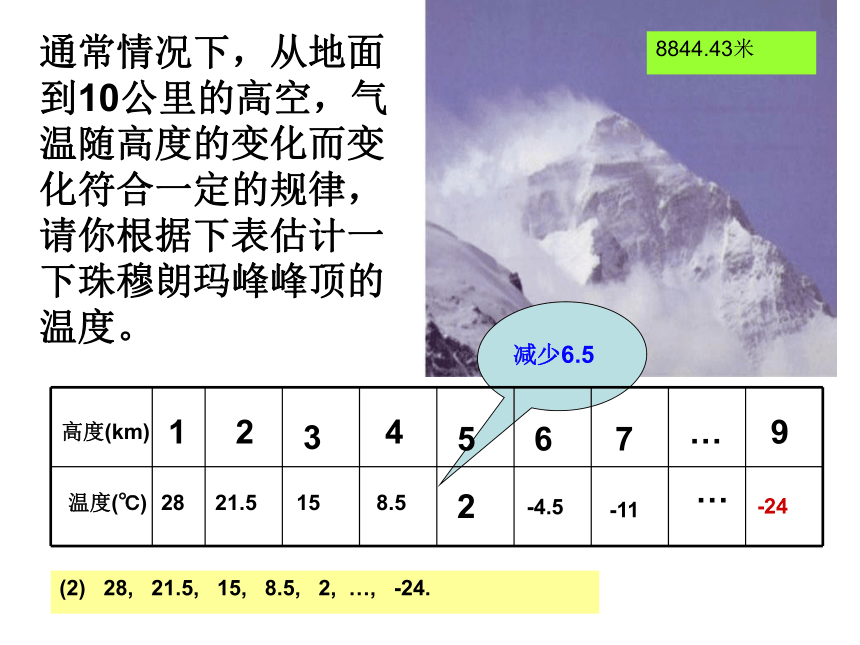
通常情况下,从地面到10公里的高空,气温随高度的变化而变化符合一定的规律,请你根据下表估计一下珠穆朗玛峰峰顶的温度。
8844.43米
(2) 28, 21.5, 15, 8.5, 2, …, -24.
减少6.5
…
高度(km)
温度(℃)
1
2
3
28
21.5
15
7
-11
4
5
8.5
2
6
-4.5
9
-24
…
(1)1682,1758,1834,1910,1986,2062
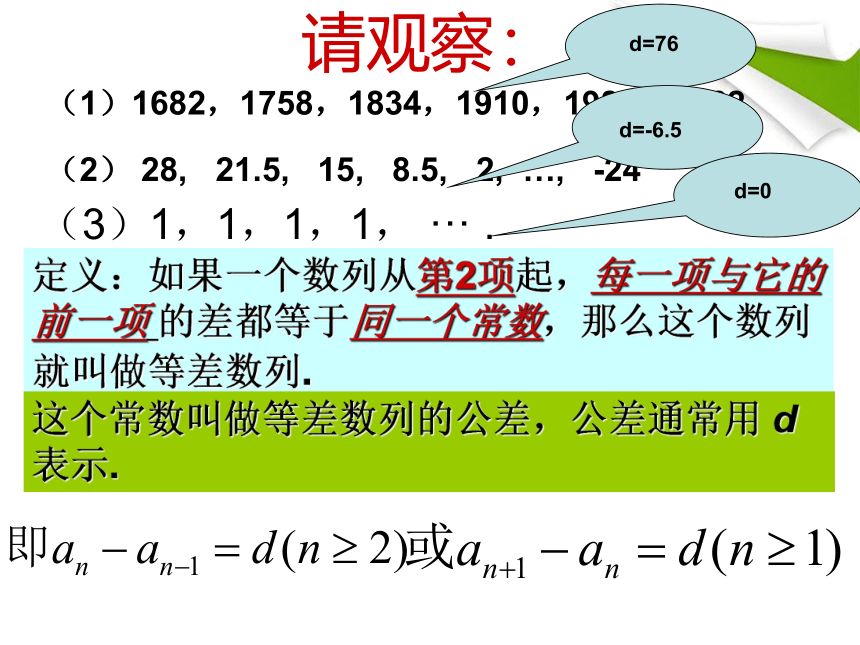
请观察:
请问:它们有什么共同特点?
(2) 28, 21.5, 15, 8.5, 2, …, -24
(3)1,1,1,1, ··· .
共同特点:从第2项起,每一项与它的前一项的差等于同一个常数。
定义:如果一个数列从第2项起,每一项与它的前一项 的差都等于同一个常数,那么这个数列就叫做等差数列.
这个常数叫做等差数列的公差,公差通常用 d 表示.
d=76
d=-6.5
d=0
是
不是
不是
练习1
判断下列各组数列中哪些是等差数列,哪些不是?如果是,写出首项a1和公差d, 如果不是,说明理由。
(1)1,3,5,7,…
(2)9,6,3,0,-3…
(3)-8,-6,-4,-2,0,…
(4)3,3,3,3,…
(6)15,12,10,8,6,…
是
是
是
a1=1,d=2
a1=9,d=-3
a1=-8,d=2
a1=3,d=0
想一想
小结:
1、判断一个数列是不是等差数列,主要是由定义进行判断 an+1-an 是不是同一个常数。
2、公差d是每一项(从第2项起)与它的前一项的差,防止把被减数与减数弄颠倒,而且公差可以是正数,负数,也可以为0。
在如下的两个数之间,插入一个什么数后这三个数就会成为一个等差数列:
(1)2 ,( ) , 4 (2)-12,( ) ,0
3
-6
如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A叫做a与b的等差中项。
思 考
( 3 ) , ( ) ,
等差中项
如果a,A,b三个数成等差数列,这时我们称A为a与b的等差中项。利用等差数列的概念可知:
不难发现,在一个等差数列中,从第
2项起,每一项(有穷数列的末项除外)
都是它的前一项与后一项的等差中项.
数列:1,3,5,7,9,11,13…
5是3和7的等差中项,1和9的等差中项;
9是7和11的等差中项,5和13的等差中项.
问题情景
观察数列:1,3,5,7,…
思 考:
在数列中a100=?我们该如何求解呢?
要是有通项公式该有多好啊!
探究1:等差数列的通项公式(迭代法)
如果一个数列
…,
…
通项公式:
归纳得:
…
等差数列的通项公式(累加法)
共n-1个式子
an-a1=(n-1)d
上述各式两边同时相加,得:
通项公式:
等差数列的通项公式
在等差数列通项公式中,有四个量,
知道其中的任意三个量,就可以求出另一个量,即知三求一 .
例1(1)求等差数列8,5,2,…的第20项;
(2)判断-401是不是等差数列 –5,-9 ,-13…的项 如果是,是第几项,如果不是,说明理由。
分析:
(1)由给出的等差数列前三项,先找到首项a1,求出公差d,写出通项公式,就可以求出第20项a20。
解:(1)由题意得:a1=8,d=5-8=-3,n=20
∴这个数列的通项公式是:
an=a1+(n-1)d=-3n+11
∴a20=11-3×20=-49
例1(1)求等差数列8,5,2,…的第20项;
(2)判断-401是不是等差数列 –5,-9 ,-13…的项 如果是,是第几项,如果不是,说明理由。
分析:
(2)要想判断-401是否为这个数列中的项,关键是要求出通项公式,看是否存在正整数n,使得an=-401。
(2)由题意得: a1=-5,d=-9-(-5)=-4
∴这个数列的通项公式是:
an=-5+ (n - 1) × (-4)=-4n-1
令-401=-4n-1,得 n=100
∴-401是这个数列的第100项。
求基本量a1和d :根据已知条件列方程,由此解出a1和d ,再代入通项公式。
像这样根据已知量和未知量之间的关系,列出方程求解的思想方法,称方程思想。
这是数学中的常用思想方法之一。
题后点评
求通项公式的关键步骤:
1. 求等差数列3,7,11,…的第4,7,10项;
解得:
2. 100是不是等差数列2,9,16,…中的项?
3. -20是不是等差数列0,-3.5,-7 …中的项;
解得:
解得:
4 . 已知等差数列 , 求:
解得:
练一练
探究2:已知等差数列{ }中,公差为d,
则 与 (n , m ∈ N*,m≠n) 有何关系?
解:由等差数列的通项公式知
①-②
①
②
(这是等差数列通项公式的推广形式 )
推广后的通项公式
(n-m)d
例2: 在等差数列{an}中
(1) 若a59=70,a80=112,求a101;
(2) 若ap=q,aq=p (p≠q),求ap+q;
(3) 若a12=23,a42=143, an=263,求n.
d=2,
a101=154
d= -1,
ap+q=0
d= 4,
n=72
(m≠n)
1、 等差数列的概念。必须从第2项起后项减去前项,并且差是同一常数。
2、等差中项的概念。三个数成等差数列,中间的数称为等差中项
课堂小结:
这节课主要讲了以下三个问题:
3、等差数列的通项公式 an = a1+(n-1)d 知道其中三 个(或两个)字母变量,可用列方程(或方程组)的方法,求余下的一个(或两个)变量。以及an= am+(n-m) d
2.2等差数列(一)
复习回顾:
1.数列定义:按照一定顺序排成的一列数,
简记作:{an}
2.通项公式:数列{an}中第n项an与n之间的关系式
3.数列的分类
(1)按项数分:
有穷数列,
(2)按项之间的大小关系:
递增数列,
递减数列,
无穷数列
摆动数列,
常数列。
4.数列的实质
5.递推公式:
如果已知{an}的第1项(或前n项),且任一项an与它的前一项an-1(或前n项)间的关系可用一个公式来表示,这个公式叫做数列的递推公式.
在过去的三百多年里,人们分别在下列时间里观测到了哈雷慧星:
(1)1682,1758,1834,1910,1986,( )
你能预测出下一次的大致时间吗?
2062
相差76
引入新课
通常情况下,从地面到10公里的高空,气温随高度的变化而变化符合一定的规律,请你根据下表估计一下珠穆朗玛峰峰顶的温度。
8844.43米
(2) 28, 21.5, 15, 8.5, 2, …, -24.
减少6.5
…
高度(km)
温度(℃)
1
2
3
28
21.5
15
7
-11
4
5
8.5
2
6
-4.5
9
-24
…
(1)1682,1758,1834,1910,1986,2062
请观察:
请问:它们有什么共同特点?
(2) 28, 21.5, 15, 8.5, 2, …, -24
(3)1,1,1,1, ··· .
共同特点:从第2项起,每一项与它的前一项的差等于同一个常数。
定义:如果一个数列从第2项起,每一项与它的前一项 的差都等于同一个常数,那么这个数列就叫做等差数列.
这个常数叫做等差数列的公差,公差通常用 d 表示.
d=76
d=-6.5
d=0
是
不是
不是
练习1
判断下列各组数列中哪些是等差数列,哪些不是?如果是,写出首项a1和公差d, 如果不是,说明理由。
(1)1,3,5,7,…
(2)9,6,3,0,-3…
(3)-8,-6,-4,-2,0,…
(4)3,3,3,3,…
(6)15,12,10,8,6,…
是
是
是
a1=1,d=2
a1=9,d=-3
a1=-8,d=2
a1=3,d=0
想一想
小结:
1、判断一个数列是不是等差数列,主要是由定义进行判断 an+1-an 是不是同一个常数。
2、公差d是每一项(从第2项起)与它的前一项的差,防止把被减数与减数弄颠倒,而且公差可以是正数,负数,也可以为0。
在如下的两个数之间,插入一个什么数后这三个数就会成为一个等差数列:
(1)2 ,( ) , 4 (2)-12,( ) ,0
3
-6
如果在a与b中间插入一个数A,使a,A,b成等差数列,那么A叫做a与b的等差中项。
思 考
( 3 ) , ( ) ,
等差中项
如果a,A,b三个数成等差数列,这时我们称A为a与b的等差中项。利用等差数列的概念可知:
不难发现,在一个等差数列中,从第
2项起,每一项(有穷数列的末项除外)
都是它的前一项与后一项的等差中项.
数列:1,3,5,7,9,11,13…
5是3和7的等差中项,1和9的等差中项;
9是7和11的等差中项,5和13的等差中项.
问题情景
观察数列:1,3,5,7,…
思 考:
在数列中a100=?我们该如何求解呢?
要是有通项公式该有多好啊!
探究1:等差数列的通项公式(迭代法)
如果一个数列
…,
…
通项公式:
归纳得:
…
等差数列的通项公式(累加法)
共n-1个式子
an-a1=(n-1)d
上述各式两边同时相加,得:
通项公式:
等差数列的通项公式
在等差数列通项公式中,有四个量,
知道其中的任意三个量,就可以求出另一个量,即知三求一 .
例1(1)求等差数列8,5,2,…的第20项;
(2)判断-401是不是等差数列 –5,-9 ,-13…的项 如果是,是第几项,如果不是,说明理由。
分析:
(1)由给出的等差数列前三项,先找到首项a1,求出公差d,写出通项公式,就可以求出第20项a20。
解:(1)由题意得:a1=8,d=5-8=-3,n=20
∴这个数列的通项公式是:
an=a1+(n-1)d=-3n+11
∴a20=11-3×20=-49
例1(1)求等差数列8,5,2,…的第20项;
(2)判断-401是不是等差数列 –5,-9 ,-13…的项 如果是,是第几项,如果不是,说明理由。
分析:
(2)要想判断-401是否为这个数列中的项,关键是要求出通项公式,看是否存在正整数n,使得an=-401。
(2)由题意得: a1=-5,d=-9-(-5)=-4
∴这个数列的通项公式是:
an=-5+ (n - 1) × (-4)=-4n-1
令-401=-4n-1,得 n=100
∴-401是这个数列的第100项。
求基本量a1和d :根据已知条件列方程,由此解出a1和d ,再代入通项公式。
像这样根据已知量和未知量之间的关系,列出方程求解的思想方法,称方程思想。
这是数学中的常用思想方法之一。
题后点评
求通项公式的关键步骤:
1. 求等差数列3,7,11,…的第4,7,10项;
解得:
2. 100是不是等差数列2,9,16,…中的项?
3. -20是不是等差数列0,-3.5,-7 …中的项;
解得:
解得:
4 . 已知等差数列 , 求:
解得:
练一练
探究2:已知等差数列{ }中,公差为d,
则 与 (n , m ∈ N*,m≠n) 有何关系?
解:由等差数列的通项公式知
①-②
①
②
(这是等差数列通项公式的推广形式 )
推广后的通项公式
(n-m)d
例2: 在等差数列{an}中
(1) 若a59=70,a80=112,求a101;
(2) 若ap=q,aq=p (p≠q),求ap+q;
(3) 若a12=23,a42=143, an=263,求n.
d=2,
a101=154
d= -1,
ap+q=0
d= 4,
n=72
(m≠n)
1、 等差数列的概念。必须从第2项起后项减去前项,并且差是同一常数。
2、等差中项的概念。三个数成等差数列,中间的数称为等差中项
课堂小结:
这节课主要讲了以下三个问题:
3、等差数列的通项公式 an = a1+(n-1)d 知道其中三 个(或两个)字母变量,可用列方程(或方程组)的方法,求余下的一个(或两个)变量。以及an= am+(n-m) d
