4.2等差数列前n项和(共17张PPT)
文档属性
| 名称 | 4.2等差数列前n项和(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 20:54:50 | ||
图片预览






文档简介
(共17张PPT)
课前准备
请同学们打开课本选择性必修第二册第18页,准备好
练习本、笔记本、笔,端正坐姿,做好上课准备.
知识回顾(在练习本上默写以下知识):
1.等差数列的定义及符号表示.
2.等差中项的概念.
3.等差数列的通项公式及推广形式.
4.重要性质.
等差数列的前n项和(1)
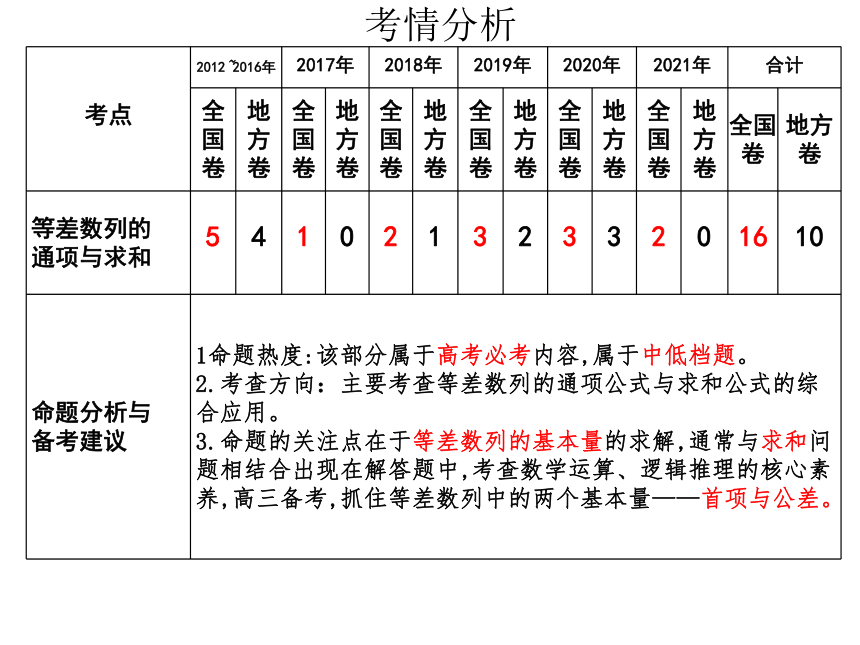
考情分析
考点 2012~2016年 2017年 2018年 2019年 2020年 2021年 合计
全国卷 地方卷 全国卷 地方卷 全国卷 地方卷 全国卷 地方卷 全国卷 地方卷 全国卷 地方卷 全国卷 地方卷
等差数列的
通项与求和 5 4 1 0 2 1 3 2 3 3 2 0 16 10
命题分析与
备考建议 1命题热度:该部分属于高考必考内容,属于中低档题。
2.考查方向:主要考查等差数列的通项公式与求和公式的综合应用。
3.命题的关注点在于等差数列的基本量的求解,通常与求和问题相结合出现在解答题中,考查数学运算、逻辑推理的核心素养,高三备考,抓住等差数列中的两个基本量——首项与公差。
学习目标
(1)探索并掌握等差数列的前n项和公式;
(2)理解等差数列的通项公式与前n项和公式的关系;
高斯出生于一个工匠家庭,幼时家境贫困,但聪敏异常.上小学四年级时,一次老师布置了一道数学习题:“把从1到100的自然数加起来,和是多少?”当其他同学忙于把100个数逐项相加时,年仅10岁的小高斯略一思索就得到答案5050,这使老师非常吃惊.那么高斯是采用了什么方法来巧妙地计算出来的呢?
高斯(1777---1855), 德国数学家、物理学家和天文学家.他和牛顿、阿基米德,被誉为有史以来的三大数学家.有“数学王子”之称.
高斯“神速求和”的故事:
首项与末项的和: 1+100=101,
第2项与倒数第2项的和: 2+99 =101,
第3项与倒数第3项的和: 3+98 =101,
· · · · · ·
第50项与倒数第50项的和:50+51=101,
于是所求的和是:
高斯算法:
1+2+3+4+· · ·+97+98+99+100=
5050
问题1
问题2
计算:1+2+3+…+100+101=
思路1(拿出中间项,再首尾配对)
原式=(1+101)+ (2+100)+ (3+99)+… + (50+52)+51
思路2(拿出末项,再首尾配对)
原式=(1+2+3+… + 100)+101
思路3 (拿出首项,再首尾配对)
原式=1+(2+3+… + 100+101)
5151
思路……
n + (n-1) + (n-2) +…+ 2 +1
那么,对一般的等差数列,如何求它的
前n项和呢?
分析:这其实是求一个具体的等差数列前n项和.
①
②
倒序相加法
问题3
①
②
倒序相加法
问题4
怎样求一般等差数列的前n项和呢?
等差数列的前n项和公式
公式1
公式2
基本量:
知三求二
如何推导?
公式记忆
—— 类比梯形面积公式记忆
结论:知 三 求 二
回扣课本 夯实双基
做学案:例1
回扣课本 夯实双基
500
2550
-130
回扣课本 夯实双基
走进高考
25
100
B
C
A
1.等差数列的前n项和公式1:
2.等差数列的前n项和公式2:
3.(1)倒序相加法求和
(2)方程思想在教学过程中的渗透
作业:
课本P23练习:第2-5题
课前准备
请同学们打开课本选择性必修第二册第18页,准备好
练习本、笔记本、笔,端正坐姿,做好上课准备.
知识回顾(在练习本上默写以下知识):
1.等差数列的定义及符号表示.
2.等差中项的概念.
3.等差数列的通项公式及推广形式.
4.重要性质.
等差数列的前n项和(1)
考情分析
考点 2012~2016年 2017年 2018年 2019年 2020年 2021年 合计
全国卷 地方卷 全国卷 地方卷 全国卷 地方卷 全国卷 地方卷 全国卷 地方卷 全国卷 地方卷 全国卷 地方卷
等差数列的
通项与求和 5 4 1 0 2 1 3 2 3 3 2 0 16 10
命题分析与
备考建议 1命题热度:该部分属于高考必考内容,属于中低档题。
2.考查方向:主要考查等差数列的通项公式与求和公式的综合应用。
3.命题的关注点在于等差数列的基本量的求解,通常与求和问题相结合出现在解答题中,考查数学运算、逻辑推理的核心素养,高三备考,抓住等差数列中的两个基本量——首项与公差。
学习目标
(1)探索并掌握等差数列的前n项和公式;
(2)理解等差数列的通项公式与前n项和公式的关系;
高斯出生于一个工匠家庭,幼时家境贫困,但聪敏异常.上小学四年级时,一次老师布置了一道数学习题:“把从1到100的自然数加起来,和是多少?”当其他同学忙于把100个数逐项相加时,年仅10岁的小高斯略一思索就得到答案5050,这使老师非常吃惊.那么高斯是采用了什么方法来巧妙地计算出来的呢?
高斯(1777---1855), 德国数学家、物理学家和天文学家.他和牛顿、阿基米德,被誉为有史以来的三大数学家.有“数学王子”之称.
高斯“神速求和”的故事:
首项与末项的和: 1+100=101,
第2项与倒数第2项的和: 2+99 =101,
第3项与倒数第3项的和: 3+98 =101,
· · · · · ·
第50项与倒数第50项的和:50+51=101,
于是所求的和是:
高斯算法:
1+2+3+4+· · ·+97+98+99+100=
5050
问题1
问题2
计算:1+2+3+…+100+101=
思路1(拿出中间项,再首尾配对)
原式=(1+101)+ (2+100)+ (3+99)+… + (50+52)+51
思路2(拿出末项,再首尾配对)
原式=(1+2+3+… + 100)+101
思路3 (拿出首项,再首尾配对)
原式=1+(2+3+… + 100+101)
5151
思路……
n + (n-1) + (n-2) +…+ 2 +1
那么,对一般的等差数列,如何求它的
前n项和呢?
分析:这其实是求一个具体的等差数列前n项和.
①
②
倒序相加法
问题3
①
②
倒序相加法
问题4
怎样求一般等差数列的前n项和呢?
等差数列的前n项和公式
公式1
公式2
基本量:
知三求二
如何推导?
公式记忆
—— 类比梯形面积公式记忆
结论:知 三 求 二
回扣课本 夯实双基
做学案:例1
回扣课本 夯实双基
500
2550
-130
回扣课本 夯实双基
走进高考
25
100
B
C
A
1.等差数列的前n项和公式1:
2.等差数列的前n项和公式2:
3.(1)倒序相加法求和
(2)方程思想在教学过程中的渗透
作业:
课本P23练习:第2-5题
