4.2等差数列求和公式课件(共18张PPT)
文档属性
| 名称 | 4.2等差数列求和公式课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 20:55:37 | ||
图片预览





文档简介
(共18张PPT)
泰姬陵坐落于印度古都阿格,是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,她宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,成为世界七大奇迹之一。陵寝以宝石镶饰,图案之细致令人叫绝。传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有100层(见上图),奢靡之程度,可见一斑。你知道这个图案一共耗费了多少宝石吗?
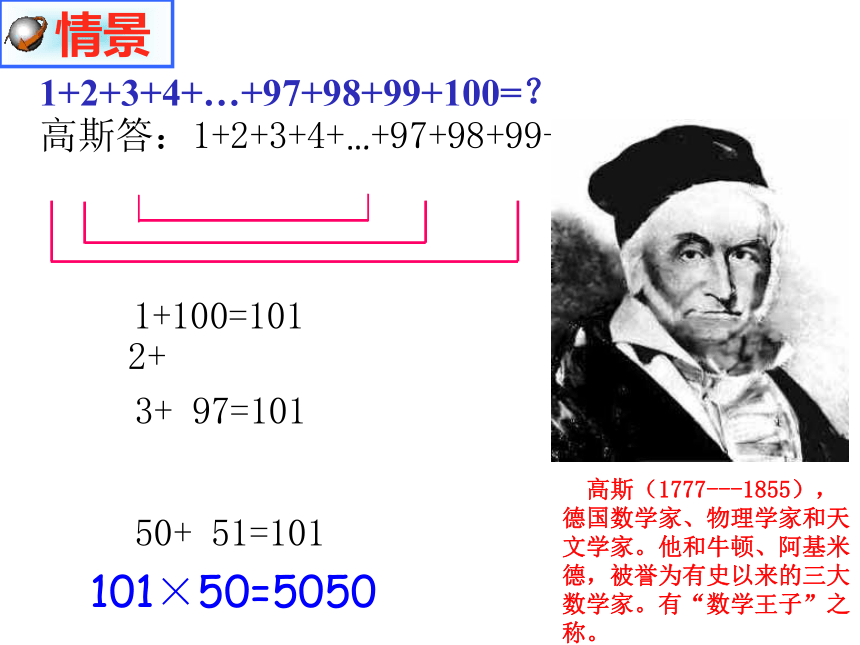
高斯答:1+2+3+4+…+97+98+99+100=
1+100=101
101×50=5050
2+ 99=101
3+ 97=101
……
50+ 51=101
5050
1+2+3+4+…+97+98+99+100=?
情景
高斯(1777---1855), 德国数学家、物理学家和天文学家。他和牛顿、阿基米德,被誉为有史以来的三大数学家。有“数学王子”之称。
实际上高斯解决了求等差数列
1,2,3,4,…n,…
前100项的和的问题
定义 一般的,我们称
a1+a2+a3+…+an
为数列{an}的前n项和,用Sn 表示,即
Sn =a1+a2+a3+…+an
如何求等差数列
1,2,3,4,…n,…
前n项的和?
sn = 1 + 2 + 3 + …+(n-1 )+ n
sn = n +( n-1 )+(n-2)+… + 2 + 1
∴2 sn =(n+ 1)+ (n+ 1) +…+(n+ 1)
=n(n+1)
思考:这种方法能否推广到求一般等差数列前n项求和呢?
+)
—— 倒序相加法
求等差数列 1,2,3,…n,…前n项的和?
由 S n = a 1 + a 2 + a 3 + … + a n -1 + a n
S n = a n + a n -1 + a n -2 + … + a 2 + a 1
+)
2S n = ( a 1 + a n ) + ( a 2 + a n -1 ) +…+ ( a n + a 1 )
=n ( a 1 + a n )
倒序相加法
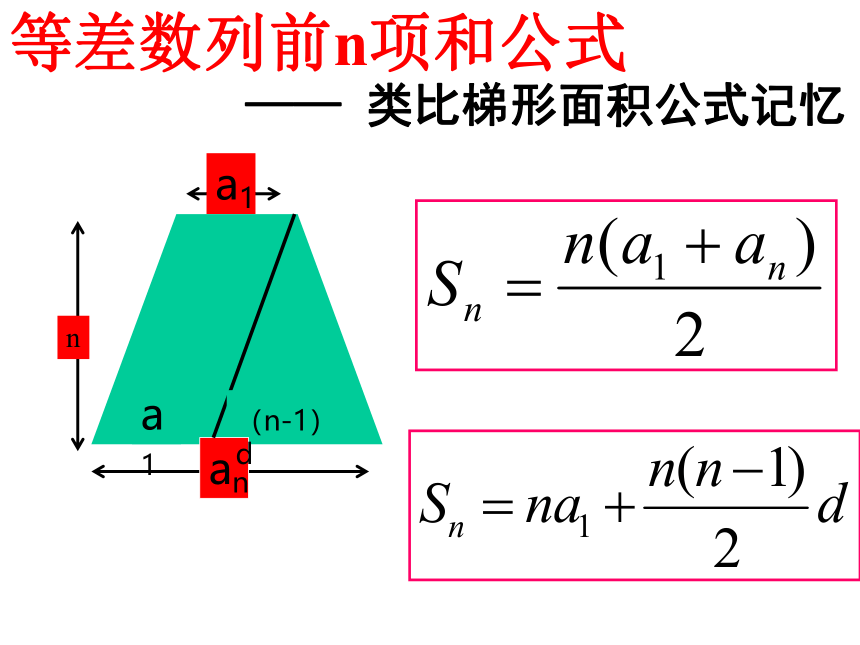
故等差数列的前 n 项求和公式:
探究发现
a1
an
n
等差数列前n项和公式
—— 类比梯形面积公式记忆
a1
(n-1)d
练习 根据下列各题中的条件,求相应的等差数列 的前n项和
答案 (1)
(2)
根据条件,选择公式
1、等差数列中a1 =4,d=2, an=32,
求 数列的前项和Sn
2、等差数列5,4,3,2,…,则前多少项的和 为 -30;
270
例1
15
巩固与提高
3. 在等差数列{an}中,已知a6+a9+a12+a15=34,S20= ————
1. 在等差数列{an}中,a2+a9=30,求S10= ———
2. 在等差数列{an}中,已知a7=20,S13 = ——
150
260
170
反思总结:
当已知条件不足以求出a1和d时,要认真观察,灵活应用等差数列的性质,看能否用整体思想求a1+an的值.
例2: 2000年11月14日教育部下发了《关于小学
“校校通”工程的通知.某市据此提出了实施
“校校通”工程的总目标:从2001年起用10年的
时间,在全市中小学建成不同标准的校园网.
据测算,2001年该市用于“校校通”工程的经费
为500万元. 为了保证工程的顺利实施,计划
每年投入的资金都比上一年增加50万元. 那么
从2001年起的未来10年内,该市在“校校通”工
程的总投入是多少?
学以致用
总结:实际问题,建立数学模型,利用数学的观点
解决问题,然后再回归问题实际
例3
公式应用
已知等差数列{an}前10项的和是310,
前20项的和是1220.由这些条件能确
定这个等差数列的前n项和的公式吗?
列方程组,解方程
例 4
已知数列 的前 项和为
(1)求数列 的通项公式;
(2)这个数列是等差数列吗?如果是,它 的首相与公差分别是什么?
Sn=n2+9n
反思:已知Sn如何求通项公式an
等差数列前n项和公式的推导:
倒序相加法
类比思想、方程思想、
数学建模思想,整体思想
数学思想:
等差数列前n项和公式的应用:
课本46页
习题2.3:1、2、
作业反馈
作业反馈
a1
an
a1
an
n
等差数列前n项和公式
—— 类比梯形面积公式记忆
方法2:等差数列{ an }a1, a2 , a3 ,…, an ,…的公差为d.
泰姬陵坐落于印度古都阿格,是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,她宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,成为世界七大奇迹之一。陵寝以宝石镶饰,图案之细致令人叫绝。传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有100层(见上图),奢靡之程度,可见一斑。你知道这个图案一共耗费了多少宝石吗?
高斯答:1+2+3+4+…+97+98+99+100=
1+100=101
101×50=5050
2+ 99=101
3+ 97=101
……
50+ 51=101
5050
1+2+3+4+…+97+98+99+100=?
情景
高斯(1777---1855), 德国数学家、物理学家和天文学家。他和牛顿、阿基米德,被誉为有史以来的三大数学家。有“数学王子”之称。
实际上高斯解决了求等差数列
1,2,3,4,…n,…
前100项的和的问题
定义 一般的,我们称
a1+a2+a3+…+an
为数列{an}的前n项和,用Sn 表示,即
Sn =a1+a2+a3+…+an
如何求等差数列
1,2,3,4,…n,…
前n项的和?
sn = 1 + 2 + 3 + …+(n-1 )+ n
sn = n +( n-1 )+(n-2)+… + 2 + 1
∴2 sn =(n+ 1)+ (n+ 1) +…+(n+ 1)
=n(n+1)
思考:这种方法能否推广到求一般等差数列前n项求和呢?
+)
—— 倒序相加法
求等差数列 1,2,3,…n,…前n项的和?
由 S n = a 1 + a 2 + a 3 + … + a n -1 + a n
S n = a n + a n -1 + a n -2 + … + a 2 + a 1
+)
2S n = ( a 1 + a n ) + ( a 2 + a n -1 ) +…+ ( a n + a 1 )
=n ( a 1 + a n )
倒序相加法
故等差数列的前 n 项求和公式:
探究发现
a1
an
n
等差数列前n项和公式
—— 类比梯形面积公式记忆
a1
(n-1)d
练习 根据下列各题中的条件,求相应的等差数列 的前n项和
答案 (1)
(2)
根据条件,选择公式
1、等差数列中a1 =4,d=2, an=32,
求 数列的前项和Sn
2、等差数列5,4,3,2,…,则前多少项的和 为 -30;
270
例1
15
巩固与提高
3. 在等差数列{an}中,已知a6+a9+a12+a15=34,S20= ————
1. 在等差数列{an}中,a2+a9=30,求S10= ———
2. 在等差数列{an}中,已知a7=20,S13 = ——
150
260
170
反思总结:
当已知条件不足以求出a1和d时,要认真观察,灵活应用等差数列的性质,看能否用整体思想求a1+an的值.
例2: 2000年11月14日教育部下发了《关于小学
“校校通”工程的通知.某市据此提出了实施
“校校通”工程的总目标:从2001年起用10年的
时间,在全市中小学建成不同标准的校园网.
据测算,2001年该市用于“校校通”工程的经费
为500万元. 为了保证工程的顺利实施,计划
每年投入的资金都比上一年增加50万元. 那么
从2001年起的未来10年内,该市在“校校通”工
程的总投入是多少?
学以致用
总结:实际问题,建立数学模型,利用数学的观点
解决问题,然后再回归问题实际
例3
公式应用
已知等差数列{an}前10项的和是310,
前20项的和是1220.由这些条件能确
定这个等差数列的前n项和的公式吗?
列方程组,解方程
例 4
已知数列 的前 项和为
(1)求数列 的通项公式;
(2)这个数列是等差数列吗?如果是,它 的首相与公差分别是什么?
Sn=n2+9n
反思:已知Sn如何求通项公式an
等差数列前n项和公式的推导:
倒序相加法
类比思想、方程思想、
数学建模思想,整体思想
数学思想:
等差数列前n项和公式的应用:
课本46页
习题2.3:1、2、
作业反馈
作业反馈
a1
an
a1
an
n
等差数列前n项和公式
—— 类比梯形面积公式记忆
方法2:等差数列{ an }a1, a2 , a3 ,…, an ,…的公差为d.
