4.22等差数列前n项和(共20张PPT)
文档属性
| 名称 | 4.22等差数列前n项和(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 21:01:34 | ||
图片预览







文档简介
(共20张PPT)
等差数列的求和公式
诱思探究1
首尾
配对
诱思探究1
诱思探究2
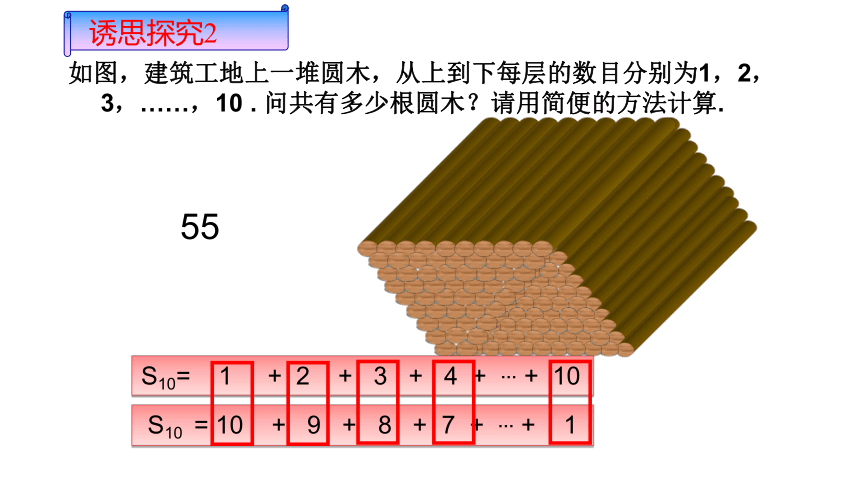
如图,建筑工地上一堆圆木,从上到下每层的数目分别为1,2,3,……,10 . 问共有多少根圆木?请用简便的方法计算.
S10= 1 + 2 + 3 + 4 + … + 10
S10 = 10 + 9 + 8 + 7 + … + 1
55
从上而下共27圈,第一圈是9块,第二层是18块,第三层是27块… …第27圈是243块地砖,共多少块地砖?
即: 9+18+27······+243=?
S27=9 + 18 + 27 + … + 243
S27 =243 + 234 + 225 + … + 9
2S27=(9+243) + (18+234) +(27+225)+ … + (243+9)
解决问题
S27=3402
这实质上就是数学中数列求和的一种重要方法
--------倒序相加法
总结一下这种方法特点?可以叫什么法呢?
问题: 对于一般等差数列{an},首项为a1公差为d,
如何推导它的前n项和公式Sn呢?
等差数列的前n项和公式推导
倒序相加法
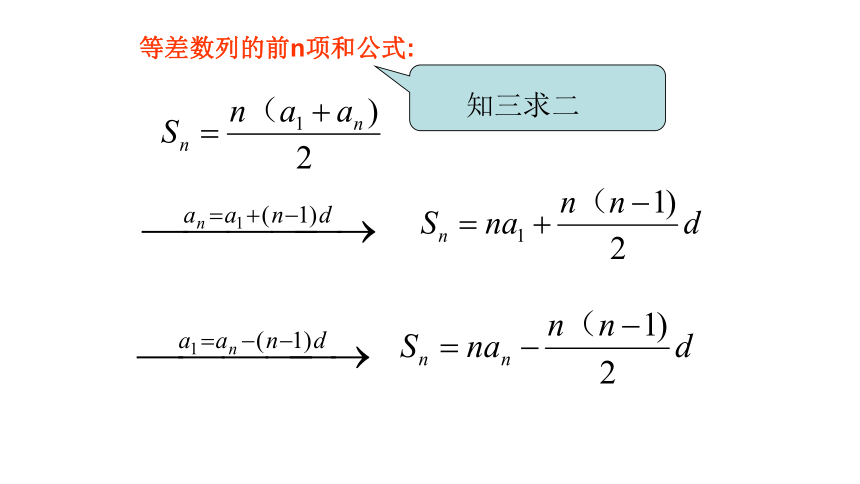
等差数列的前n项和公式:
知三求二
公式的记忆
我们可结合梯形的面积公式来记忆等差数列前 n 项和公式.
n
a1
an
公式应用
根据下列各题中的条件,求相应的等差数列{an}的Sn :
(1)a1=5,an=95,n=10
(2)a1=100,d=-2,n=50
变式练习
一个屋顶的某一斜面成等腰梯形,最上面一层铺瓦片21块,往下每一层多铺1块,斜面上铺了19层,共铺瓦片多少块?
解:由题意,该屋顶斜面每层所铺的瓦片数构成等差数列{an},且a1=21,d=1,n=19.
于是,屋顶斜面共铺瓦片:
答:屋顶斜面共铺瓦片570块.
例题讲解
例2、已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n项和的公式吗?
解:由于S10=310,S20=1220,将它们代入公式
可得
所以
例题讲解
例2、已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n项和的公式吗?
另解:
两式相减得
将等差数列前n项和公式
看作是一个关于n的函数,这个函数有什么特点?
当d≠0时,Sn是常数项为零的二次函数
则 Sn=An2+Bn
令
等差数列的前n项和表达式与函数有什么关系?
结论:
q
pn
a
qn
pn
S
q
p
a
a
p
r
q
p
r
qn
pn
S
a
n
n
n
n
n
n
+
=
+
=
=
+
+
=
{an}
2
}
{
0
r
}
{
0
r
)
0
(
n
}
{
)
1
(
2
2
成等差数列
数列
为常数
、
)
(
不是等差数列
时,数列
当
一定是等差数列
时,数列
当
为常数,且
、
、
项和
的前
若数列
课堂练习
答案: 27
练习1、
练习2、等差数列-10,-6,-2,2,
…的前______项的和为54?
答案: n=9,或n=-3(舍去)
仍是知三求一
课堂小结
1.等差数列前n项和的公式;
2.等差数列前n项和公式的推导方法——倒序相加法;
3.在两个求和公式中,各有五个元素,只要知道其中三个元素,结合通项公式就可求出另两个元素.
知识打包
an=a1+(n-1)d
对于Sn、an 、a1、n、d 五个量,“知三求二”.
方程(组)思想
(待定系数法)
倒序求和法
掌握与应用
教材P22 练习 1.2.3.4.
1.一个等差数列前4项的和是24,前5项的和与前2项的和的差是27,求这个等差数列的通项公式.
2.差数列{ }中, =-15, 公差d=3, 求数列{ }的前n项和的最小值.
课后作业
等差数列的求和公式
诱思探究1
首尾
配对
诱思探究1
诱思探究2
如图,建筑工地上一堆圆木,从上到下每层的数目分别为1,2,3,……,10 . 问共有多少根圆木?请用简便的方法计算.
S10= 1 + 2 + 3 + 4 + … + 10
S10 = 10 + 9 + 8 + 7 + … + 1
55
从上而下共27圈,第一圈是9块,第二层是18块,第三层是27块… …第27圈是243块地砖,共多少块地砖?
即: 9+18+27······+243=?
S27=9 + 18 + 27 + … + 243
S27 =243 + 234 + 225 + … + 9
2S27=(9+243) + (18+234) +(27+225)+ … + (243+9)
解决问题
S27=3402
这实质上就是数学中数列求和的一种重要方法
--------倒序相加法
总结一下这种方法特点?可以叫什么法呢?
问题: 对于一般等差数列{an},首项为a1公差为d,
如何推导它的前n项和公式Sn呢?
等差数列的前n项和公式推导
倒序相加法
等差数列的前n项和公式:
知三求二
公式的记忆
我们可结合梯形的面积公式来记忆等差数列前 n 项和公式.
n
a1
an
公式应用
根据下列各题中的条件,求相应的等差数列{an}的Sn :
(1)a1=5,an=95,n=10
(2)a1=100,d=-2,n=50
变式练习
一个屋顶的某一斜面成等腰梯形,最上面一层铺瓦片21块,往下每一层多铺1块,斜面上铺了19层,共铺瓦片多少块?
解:由题意,该屋顶斜面每层所铺的瓦片数构成等差数列{an},且a1=21,d=1,n=19.
于是,屋顶斜面共铺瓦片:
答:屋顶斜面共铺瓦片570块.
例题讲解
例2、已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n项和的公式吗?
解:由于S10=310,S20=1220,将它们代入公式
可得
所以
例题讲解
例2、已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定求其前n项和的公式吗?
另解:
两式相减得
将等差数列前n项和公式
看作是一个关于n的函数,这个函数有什么特点?
当d≠0时,Sn是常数项为零的二次函数
则 Sn=An2+Bn
令
等差数列的前n项和表达式与函数有什么关系?
结论:
q
pn
a
qn
pn
S
q
p
a
a
p
r
q
p
r
qn
pn
S
a
n
n
n
n
n
n
+
=
+
=
=
+
+
=
{an}
2
}
{
0
r
}
{
0
r
)
0
(
n
}
{
)
1
(
2
2
成等差数列
数列
为常数
、
)
(
不是等差数列
时,数列
当
一定是等差数列
时,数列
当
为常数,且
、
、
项和
的前
若数列
课堂练习
答案: 27
练习1、
练习2、等差数列-10,-6,-2,2,
…的前______项的和为54?
答案: n=9,或n=-3(舍去)
仍是知三求一
课堂小结
1.等差数列前n项和的公式;
2.等差数列前n项和公式的推导方法——倒序相加法;
3.在两个求和公式中,各有五个元素,只要知道其中三个元素,结合通项公式就可求出另两个元素.
知识打包
an=a1+(n-1)d
对于Sn、an 、a1、n、d 五个量,“知三求二”.
方程(组)思想
(待定系数法)
倒序求和法
掌握与应用
教材P22 练习 1.2.3.4.
1.一个等差数列前4项的和是24,前5项的和与前2项的和的差是27,求这个等差数列的通项公式.
2.差数列{ }中, =-15, 公差d=3, 求数列{ }的前n项和的最小值.
课后作业
