4.2.2等差数列的前n项和公式(18张PPT)
文档属性
| 名称 | 4.2.2等差数列的前n项和公式(18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 14.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 00:00:00 | ||
图片预览






文档简介
4.2.2等差数列的前n项和公式
复习巩固
1. 等差数列定义:
2. 等差数列通项公式:
(2) an=am+(n-m)d .
(3) an=pn+q (p、q是常数)
(1) an=a1+(n-1)d (n≥1).
an-an-1 =d (n≥2)
或 an+1-an =d.
3. 几种计算公差d的方法:
复习巩固
4. 等差中项
a,A,b组成等差数列
?A=????+?????2
?
m+n=p+q ? am+an=ap+aq .
(m,n,p,q∈N*)
5. 等差数列的性质
m+n=2p ? am+an=2ap
泰姬陵坐落于印度古都阿格,是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,她宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,成为世界七大奇迹之一。陵寝以宝石镶饰,图案之细致令人叫绝.
传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有100层(见左图),奢靡之程度,可见一斑。你知道这个图案一共花了多少宝石吗?
探究新知
1+2+3+···+100 = ?
合作探究
德国古代著名数学家高斯9岁的时候很快就解决了这个问题:1+2+3+…+100=?你知道高斯是怎样算出来的吗?
高斯的算法是:
首项与末项的和:
第2项与倒数第2项的和:
第3项与倒数第3项的和:
第50项与倒数第50项的和:
…
于是所求的和是:101× =5050
1+100=101
2+99 =101
3+98 =101
50+51=101
合作探究
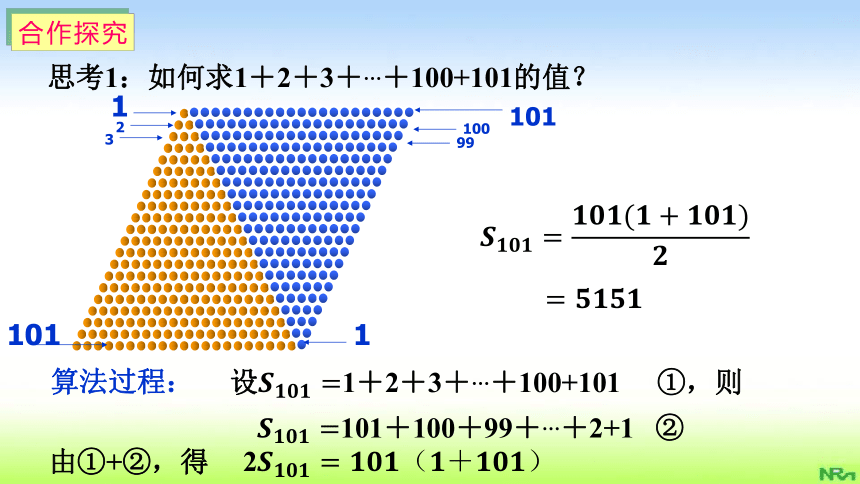
思考1:如何求1+2+3+…+100+101的值?
1
2
3
101
101
100
99
1
????????????????=????????????(????+????????????)????
?
=????????????????
?
算法过程:
设????????????????=1+2+3+…+100+101 ①,则
?
???????????????????=101+100+99+…+2+1 ②
?
由①+②,得
2????????????????=????????????(????+????????????)
?
思考2:已知数列{an}是等差数列,如何求
????????=????1+????2+????3+···+?????????1+????????的值?
?
合作探究
因为数列{an}是等差数列,
所以a1+ an= a2+ an-1= a3+ an-3 =···,
由?????????=????1+????2+????3+···+?????????1+???????? ①,得
?
????????=????????+?????????1+?????????2+···+????2+????1 ②,
?
由①+②,得
?
2????????=????(????1+???????? )
?
所以????????=????(????????+????????)?????
?
倒序相加法
如果一个数列{an},与首末项等距的两项之和等于首末两项之和,可采用把正着写和与倒着写和的两个和式相加,就得到这个数列的和,这一求和方法称为倒序相加法.
解惑提高
等差数列{an}的前n项和公式
名师点析:(1)两个公式均为等差数列的求和公式,一共涉及a1,an,Sn,n,d五个量.通常已知其中三个,可求其余两个,而且方法就是解方程(组),这也是等差数列的基本问题形式之一.
(2)当已知首项a1,末项an,项数n时,用公式Sn=????(????????+????????)????.用此公式时,有时要结合等差数列的性质,如a1+an=ak+an-k+1,从而有Sn=????????(ak+an-k+1).
?
1.①在正整数列中,前n个数的和是多少?
②在正整数列中,前n个偶数的和是多少?
1+2+…+n =
2 + 4 +…+ 2n=
2
n(n+1)
n(n+1)
小试牛刀
B
典型例题
例1 已知数列{an}是等差数列.
(1)若a1=7,a50=101,求S50; (2)若a1=2,a2=????????,求S10;
(3)若a1=????????,d=-????????, Sn =-5,求n.
?
解: (1) ????????????=????????(????????+????????????)????
?
=????????(????+????????????)????
?
=????????????????
?
(2) ????=????????-????????=????????-2=????????
?
????????????=????????????????+????????×????????d
?
=???????? ×?2+????????×???????? ×????????
?
=????????????
?
典型例题
例1 已知数列{an}是等差数列.
(1)若a1=7,a50=101,求S50; (2)若a1=2,a2=????????,求S10;
(3)若a1=????????,d=-????????, Sn =-5,求n.
?
解: (3)由????????=????????????+????×(?????????)????d,得
?
?????=????????n+????×(?????????)???? ×(?????????)
?
整理,得
????????-7n-60=0
?
解得
n=12或n=-5(舍去)
所以
n=12
解惑提高
求数列的基本量的基本方法
求数列的基本量的基本方法是构建方程或方程组或运用数列的有关性质进行处理.
(1)“知三求一”:a1,d,n称为等差数列的三个基本量,在通项公式和前n项和公式中,都含有四个量,已知其中的三个可求出第四个.
(2)“知三求二”:五个量a1,d,n,an,Sn中可知三求二,一般列方程组求解.
巩固练习
根据条件,求相应等差数列{an}的Sn:
①a1=5, an=95, n=10;
②a1=100, d=-2, n=50;
③a1=14.5, d=0.7, an=32.
答案:①500;
②2550;
③604.5
典型例题
例2 己知一个等差数列{an}前10项的和是310,前20项的和是1220.由这些条件能确定这个等差数列的首项和公差吗?
解:由题意知
????10=310,????20=1220
?
∴10????1+????????×????????????=31020????1+????????×????????????????=1220
?
解得:????1=4????=6
?
所以,由所给的条件可以确定等差数列的首项和公差.
典型例题
例2 己知一个等差数列{an}前10项的和是310,前20项的和是1220.由这些条件能确定这个等差数列的首项和公差吗?
变 式
1.己知一个等差数列{an}前10项的和是310,前20项的和是1220.求数列{an}前30项的和.
????1=4,????=6
?
????????????=????????????????
?
2.己知一个等差数列{an}前10项的和是310,前20项的和是1220.求数列{an}前n项的和.
????????=????????????+n
?
等差数列-10,-6,-2,2,…前多少项的和是54?
解:由已知可得:a1= -10,d=4
所以数列前9项的和是54.
巩固练习
课堂小结
等差数列前n项和公式
在两个求和公式中,共有五个元素,只要知道其中三个元素,结合通项公式就可求出另两个元素.
公式的推证用的是倒序相加法
(关于n的二次函数)
复习巩固
1. 等差数列定义:
2. 等差数列通项公式:
(2) an=am+(n-m)d .
(3) an=pn+q (p、q是常数)
(1) an=a1+(n-1)d (n≥1).
an-an-1 =d (n≥2)
或 an+1-an =d.
3. 几种计算公差d的方法:
复习巩固
4. 等差中项
a,A,b组成等差数列
?A=????+?????2
?
m+n=p+q ? am+an=ap+aq .
(m,n,p,q∈N*)
5. 等差数列的性质
m+n=2p ? am+an=2ap
泰姬陵坐落于印度古都阿格,是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,她宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,成为世界七大奇迹之一。陵寝以宝石镶饰,图案之细致令人叫绝.
传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有100层(见左图),奢靡之程度,可见一斑。你知道这个图案一共花了多少宝石吗?
探究新知
1+2+3+···+100 = ?
合作探究
德国古代著名数学家高斯9岁的时候很快就解决了这个问题:1+2+3+…+100=?你知道高斯是怎样算出来的吗?
高斯的算法是:
首项与末项的和:
第2项与倒数第2项的和:
第3项与倒数第3项的和:
第50项与倒数第50项的和:
…
于是所求的和是:101× =5050
1+100=101
2+99 =101
3+98 =101
50+51=101
合作探究
思考1:如何求1+2+3+…+100+101的值?
1
2
3
101
101
100
99
1
????????????????=????????????(????+????????????)????
?
=????????????????
?
算法过程:
设????????????????=1+2+3+…+100+101 ①,则
?
???????????????????=101+100+99+…+2+1 ②
?
由①+②,得
2????????????????=????????????(????+????????????)
?
思考2:已知数列{an}是等差数列,如何求
????????=????1+????2+????3+···+?????????1+????????的值?
?
合作探究
因为数列{an}是等差数列,
所以a1+ an= a2+ an-1= a3+ an-3 =···,
由?????????=????1+????2+????3+···+?????????1+???????? ①,得
?
????????=????????+?????????1+?????????2+···+????2+????1 ②,
?
由①+②,得
?
2????????=????(????1+???????? )
?
所以????????=????(????????+????????)?????
?
倒序相加法
如果一个数列{an},与首末项等距的两项之和等于首末两项之和,可采用把正着写和与倒着写和的两个和式相加,就得到这个数列的和,这一求和方法称为倒序相加法.
解惑提高
等差数列{an}的前n项和公式
名师点析:(1)两个公式均为等差数列的求和公式,一共涉及a1,an,Sn,n,d五个量.通常已知其中三个,可求其余两个,而且方法就是解方程(组),这也是等差数列的基本问题形式之一.
(2)当已知首项a1,末项an,项数n时,用公式Sn=????(????????+????????)????.用此公式时,有时要结合等差数列的性质,如a1+an=ak+an-k+1,从而有Sn=????????(ak+an-k+1).
?
1.①在正整数列中,前n个数的和是多少?
②在正整数列中,前n个偶数的和是多少?
1+2+…+n =
2 + 4 +…+ 2n=
2
n(n+1)
n(n+1)
小试牛刀
B
典型例题
例1 已知数列{an}是等差数列.
(1)若a1=7,a50=101,求S50; (2)若a1=2,a2=????????,求S10;
(3)若a1=????????,d=-????????, Sn =-5,求n.
?
解: (1) ????????????=????????(????????+????????????)????
?
=????????(????+????????????)????
?
=????????????????
?
(2) ????=????????-????????=????????-2=????????
?
????????????=????????????????+????????×????????d
?
=???????? ×?2+????????×???????? ×????????
?
=????????????
?
典型例题
例1 已知数列{an}是等差数列.
(1)若a1=7,a50=101,求S50; (2)若a1=2,a2=????????,求S10;
(3)若a1=????????,d=-????????, Sn =-5,求n.
?
解: (3)由????????=????????????+????×(?????????)????d,得
?
?????=????????n+????×(?????????)???? ×(?????????)
?
整理,得
????????-7n-60=0
?
解得
n=12或n=-5(舍去)
所以
n=12
解惑提高
求数列的基本量的基本方法
求数列的基本量的基本方法是构建方程或方程组或运用数列的有关性质进行处理.
(1)“知三求一”:a1,d,n称为等差数列的三个基本量,在通项公式和前n项和公式中,都含有四个量,已知其中的三个可求出第四个.
(2)“知三求二”:五个量a1,d,n,an,Sn中可知三求二,一般列方程组求解.
巩固练习
根据条件,求相应等差数列{an}的Sn:
①a1=5, an=95, n=10;
②a1=100, d=-2, n=50;
③a1=14.5, d=0.7, an=32.
答案:①500;
②2550;
③604.5
典型例题
例2 己知一个等差数列{an}前10项的和是310,前20项的和是1220.由这些条件能确定这个等差数列的首项和公差吗?
解:由题意知
????10=310,????20=1220
?
∴10????1+????????×????????????=31020????1+????????×????????????????=1220
?
解得:????1=4????=6
?
所以,由所给的条件可以确定等差数列的首项和公差.
典型例题
例2 己知一个等差数列{an}前10项的和是310,前20项的和是1220.由这些条件能确定这个等差数列的首项和公差吗?
变 式
1.己知一个等差数列{an}前10项的和是310,前20项的和是1220.求数列{an}前30项的和.
????1=4,????=6
?
????????????=????????????????
?
2.己知一个等差数列{an}前10项的和是310,前20项的和是1220.求数列{an}前n项的和.
????????=????????????+n
?
等差数列-10,-6,-2,2,…前多少项的和是54?
解:由已知可得:a1= -10,d=4
所以数列前9项的和是54.
巩固练习
课堂小结
等差数列前n项和公式
在两个求和公式中,共有五个元素,只要知道其中三个元素,结合通项公式就可求出另两个元素.
公式的推证用的是倒序相加法
(关于n的二次函数)
