19.2.3 第1课时 一次函数与一元一次方程、不等式 课件(共18张PPT)
文档属性
| 名称 | 19.2.3 第1课时 一次函数与一元一次方程、不等式 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-01 08:36:06 | ||
图片预览






文档简介
(共18张PPT)
人教版八下数学
精品同步教学课件
19.2.3 一次函数
第1课时一次函数与一元一次方程、不等式
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
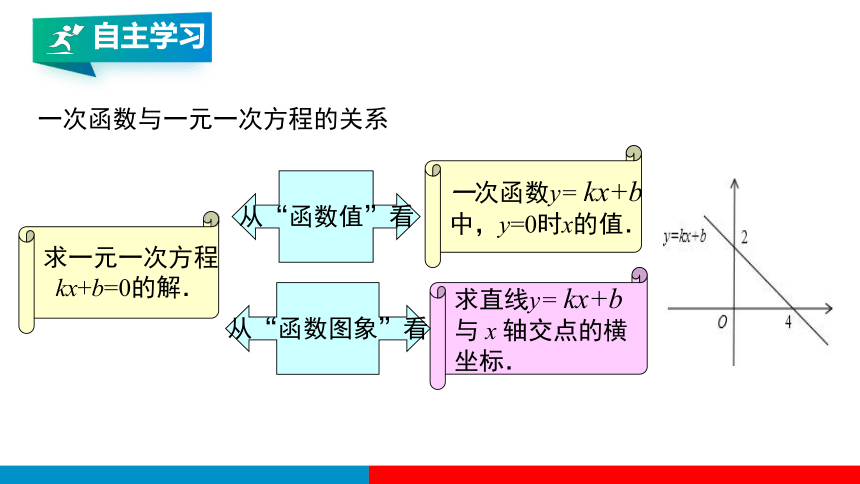
一次函数与一元一次方程(不等式)的关系
1
思考
下面3个方程有什么共同点和不同点?你能从函
数的角度对解这3个方程进行解释吗?
(1)2x+1=3; (2)2x+1=0; (3)2x+1=-1.
自主学习
可以看出,这3个方程的等号左边都是2x+1,等号右边分别是3, 0, -1.从函数的角度看,解这3个方程
相当于在一次函数y= 2x+1的函数
值分别为3, 0,-1时,求自变量x的
值.或者说,在直线y= 2x+1上取纵
坐标分别为3,0,-1的点,看它们的
横坐标分别为多少(如图).
因为任何一个以x为未知数的一
元一次方程都可以变形为ax+b=0(a≠0)的形式,所以解
一元一次方程相当于在某个一次函数y=ax+b的函数值为
0时,求自变量x的值.
自主学习
求一元一次方程
kx+b=0的解.
一次函数与一元一次方程的关系
一次函数y= kx+b
中,y=0时x的值.
从“函数值”看
求直线y= kx+b
与 x 轴交点的横
坐标.
从“函数图象”看
自主学习
1.直线y=2x+20与x轴交点坐标为(____,_____),这说明方程2x+20=0的解是x=_____.
-10
0
-10
练一练
2.若方程kx+2=0的解是x=5,则直线y=kx+2与x轴交点坐标为(____,_____).
5
0
课堂练习
思考
下面3个不等式有什么共同点和不同点?你能从
函数的角度对解这3个不等式进行解释吗?
(1)3x+2>2; (2) 3x+2<0; (3) 3x+2<-1.
自主学习
可以看出,这3个不等式的不等号左边
都是3x+2,而不等号及不等号右边却有不同.
从函数的角度看,解这3个不等式相当于在
一次函数y=3x+2的函数值分别大于2、小于
0、小于-1时,求自变量x的取值范围.或者
说,在直线y=3x+2上取纵坐标分别满足大
于2、小于0、小于-1的点,看它们的横坐
标分别满足什么条件(如图).
自主学习
例 结合函数y=-3x+6的图象求:
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当0x
O
B(2,0)
A(0,6)
y
解:(1)由图象可知,不等式
-3x+6>0 的解集是图象位于 x轴上方的x的取值范围,即x<2;不等式 -3x+6<0的解集是图象位于 x轴下方的x的取值范围,即x>2;
求kx+b>0(或<0)
(k≠0)的解集
y=kx+b的函数值
大于(或小于)0时,
x的取值范围
从“函数值”看
确定直线y=kx+b
在x轴上方(或下方)
的图象所对应的x
取值范围
从“函数图象”看
一次函数与一元一次不等式的关系
自主学习
例
已知函数y1=2x-5,y2=3-2x,求当x取何值时,
(1)y1>y2; (2)y1=y2; (3)y1<y2.
导引:
解这类题目的关键,是要将比较函数值的大小的问
题转化成解不等式的问题.
典例分析
解:
方法一:代数法.
(1)y1>y2,即2x-5>3-2x,解得x>2;
(2)y1=y2,即2x-5=3-2x,解得x=2;
(3)y1<y2,即2x-5<3-2x,解得x<2.
所以当x>2时,y1>y2;当x=2时,y1=y2;
当x<2时,y1<y2.
典例分析
方法二:图象法.
在同一直角坐标系内画出函数
y1=2x-5和y2=3-2x的图象,
如图所示.由图象知,两直线
的交点坐标为(2,-1).观察
图象可知,当x>2时,y1>y2;
当x=2时,y1=y2;
当x<2时,y1<y2.
典例分析
归 纳
根据问题可寻找代数法和图象法两种途径,用
代数法将其转化为解不等式,用图象法确定一元一
次不等式的解集的方法是:先找出直线与坐标轴的
交点,画出函数的图象,再观察图象,确定两条直
线的交点坐标,最后观察图象交点两侧直线的位置,
直接得出不等式的解集.
1.
【中考·合肥】已知方程 x+b=0的解是x=
-2,下列可能为直线y= x+b的图象的是
( )
C
课堂练习
2.
已知一次函数y=2x+n的图象如图所示,则方程2x+n=0的解可能是( )
A.x=1
B.x=
C.x=-
D.x=-1
C
课堂练习
https://www.21cnjy.com/help/help_extract.php
人教版八下数学
精品同步教学课件
19.2.3 一次函数
第1课时一次函数与一元一次方程、不等式
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
一次函数与一元一次方程(不等式)的关系
1
思考
下面3个方程有什么共同点和不同点?你能从函
数的角度对解这3个方程进行解释吗?
(1)2x+1=3; (2)2x+1=0; (3)2x+1=-1.
自主学习
可以看出,这3个方程的等号左边都是2x+1,等号右边分别是3, 0, -1.从函数的角度看,解这3个方程
相当于在一次函数y= 2x+1的函数
值分别为3, 0,-1时,求自变量x的
值.或者说,在直线y= 2x+1上取纵
坐标分别为3,0,-1的点,看它们的
横坐标分别为多少(如图).
因为任何一个以x为未知数的一
元一次方程都可以变形为ax+b=0(a≠0)的形式,所以解
一元一次方程相当于在某个一次函数y=ax+b的函数值为
0时,求自变量x的值.
自主学习
求一元一次方程
kx+b=0的解.
一次函数与一元一次方程的关系
一次函数y= kx+b
中,y=0时x的值.
从“函数值”看
求直线y= kx+b
与 x 轴交点的横
坐标.
从“函数图象”看
自主学习
1.直线y=2x+20与x轴交点坐标为(____,_____),这说明方程2x+20=0的解是x=_____.
-10
0
-10
练一练
2.若方程kx+2=0的解是x=5,则直线y=kx+2与x轴交点坐标为(____,_____).
5
0
课堂练习
思考
下面3个不等式有什么共同点和不同点?你能从
函数的角度对解这3个不等式进行解释吗?
(1)3x+2>2; (2) 3x+2<0; (3) 3x+2<-1.
自主学习
可以看出,这3个不等式的不等号左边
都是3x+2,而不等号及不等号右边却有不同.
从函数的角度看,解这3个不等式相当于在
一次函数y=3x+2的函数值分别大于2、小于
0、小于-1时,求自变量x的取值范围.或者
说,在直线y=3x+2上取纵坐标分别满足大
于2、小于0、小于-1的点,看它们的横坐
标分别满足什么条件(如图).
自主学习
例 结合函数y=-3x+6的图象求:
(1)不等式-3x+6>0 和-3x+6<0的解集;
(2)当0
O
B(2,0)
A(0,6)
y
解:(1)由图象可知,不等式
-3x+6>0 的解集是图象位于 x轴上方的x的取值范围,即x<2;不等式 -3x+6<0的解集是图象位于 x轴下方的x的取值范围,即x>2;
求kx+b>0(或<0)
(k≠0)的解集
y=kx+b的函数值
大于(或小于)0时,
x的取值范围
从“函数值”看
确定直线y=kx+b
在x轴上方(或下方)
的图象所对应的x
取值范围
从“函数图象”看
一次函数与一元一次不等式的关系
自主学习
例
已知函数y1=2x-5,y2=3-2x,求当x取何值时,
(1)y1>y2; (2)y1=y2; (3)y1<y2.
导引:
解这类题目的关键,是要将比较函数值的大小的问
题转化成解不等式的问题.
典例分析
解:
方法一:代数法.
(1)y1>y2,即2x-5>3-2x,解得x>2;
(2)y1=y2,即2x-5=3-2x,解得x=2;
(3)y1<y2,即2x-5<3-2x,解得x<2.
所以当x>2时,y1>y2;当x=2时,y1=y2;
当x<2时,y1<y2.
典例分析
方法二:图象法.
在同一直角坐标系内画出函数
y1=2x-5和y2=3-2x的图象,
如图所示.由图象知,两直线
的交点坐标为(2,-1).观察
图象可知,当x>2时,y1>y2;
当x=2时,y1=y2;
当x<2时,y1<y2.
典例分析
归 纳
根据问题可寻找代数法和图象法两种途径,用
代数法将其转化为解不等式,用图象法确定一元一
次不等式的解集的方法是:先找出直线与坐标轴的
交点,画出函数的图象,再观察图象,确定两条直
线的交点坐标,最后观察图象交点两侧直线的位置,
直接得出不等式的解集.
1.
【中考·合肥】已知方程 x+b=0的解是x=
-2,下列可能为直线y= x+b的图象的是
( )
C
课堂练习
2.
已知一次函数y=2x+n的图象如图所示,则方程2x+n=0的解可能是( )
A.x=1
B.x=
C.x=-
D.x=-1
C
课堂练习
https://www.21cnjy.com/help/help_extract.php
