19.2.3 第2课时一次函数与二元一次方程(组) 课件(共23张PPT)
文档属性
| 名称 | 19.2.3 第2课时一次函数与二元一次方程(组) 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-01 08:33:21 | ||
图片预览








文档简介
(共23张PPT)
人教版八下数学
精品同步教学课件
19.2.3 一次函数
第2课时 一次函数与二元一次方程(组)
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
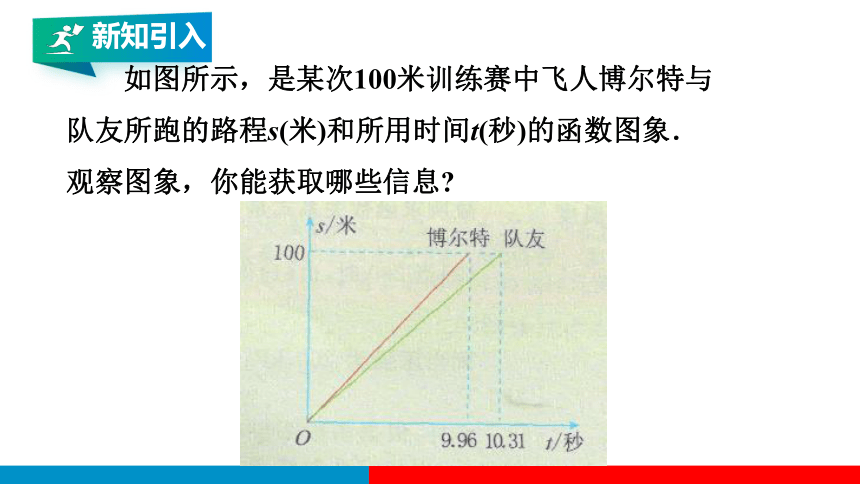
如图所示,是某次100米训练赛中飞人博尔特与
队友所跑的路程s(米)和所用时间t(秒)的函数图象.
观察图象,你能获取哪些信息
新知引入
一次函数与二元一次方程(组)的关系
1
二元一次方程与一次函数的联系
(1)任意一个二元一次方程都可化成y=kx+b的形式,
即令每个二元一次方程都对应一个一次函数,也
对应一条直线.
(2)直线y=kx+b上每一点的坐标均为这个二元一次
方程的解.
自主学习
例 1
如图所示的四条直线,其中直线上每个点的坐标都是
二元一次方程x-2y=2的解的是( )
C
典例分析
导引:
对于二元一次方程x-2y=2,当x=0时,y=-1;
当y=0时,x=2,故直线x-2y=2与两坐标轴的交点是
(0,-1),(2,0),对照四个选项中的直线,可知选C.
典例分析
归 纳
直线y=kx+b与x轴的交点的横坐标即是二元一
次方程y=kx+b中,当y=0时x的值;
直线y=kx+b与y轴的交点的纵坐标即是二元一
次方程y=kx+b中,当x=0时y的值.
解这类题,常运用数形结合思想.
问题
1号探测气球从海拔5m处出发,以1m/min的速度
上升.与此同时,2号探测气球从海拔15 m处出发,以
0.5 m/min的速度上升.两个气球都上升了1 h.
(1)用式子分别表示两个气球所在位置的海拔y (单位:m)
关于上升时间x(单位:min)的函数关系;
(2)在某时刻两个气球能否位于同一高度?如果能,这
时气球上升了多长时间?位于什么高度?
自主学习
(1)气球上升时间x满足0≤x≤60.
对于1号气球,y关于x的函数解析式为y=x+5.
对于2号气球,y关于x的函数解析式为y=0.5x+15.
(2)在某时刻两个气球位于同一高度,就是说对于x的某个值 (0≤x≤60),函数y=x+5和y=0.5x+15有相同的值y.如能求出这个x和y,则问题得到解决.由此容易想到解二元一次方程组
这就是说,当上升20 min时,两个气球都位于海拔25 m的高度.
分析:
自主学习
我们也可以用一次函数的图
象解释上述问题 的解答.如图,在
同一直角坐标系中,画出一次函
数y=x+5和y=0.5x+15的图象.
这两条直线的交点坐标为(20, 25),
这也说明当上升20 min时,两个
气球都位于海拔25 m的高度.
自主学习
一般地,因为每个含有未知数x和y的二元一次方程,
都可以改写为y=kx+b(k、b是常数,k≠0)的形式,所以每个这样的方程都对应一个一次函数,于是也对应一条直线.
这条直线上每个点的坐标(x,y)都是这个二元一次方程的解.
自主学习
由上可知,由含有未知数x和y的两个二元一次
方程组成的每个二元一 次方程组,都对应两个一次
函数,于是也对应两条直线.从“数”的角度看, 解
这样的方程组,相当于求自变量为何值时相应的两
个函数值相等,以及这个函数值是多少;从“形”
的角度看,解这样的方程组,相当于确定两条相应
直线交点的坐标.因此,我们可以用画一次函数图象
的方法得到方程组的解.
自主学习
二元一次方程组与一次函数的关系:
(1)二元一次方程组中的每个方程均可看作函数解析式.
(2)求二元一次方程组的解可看作求两个一次函数的交
点坐标.
自主学习
例2
利用图象法解二元一次方程组:
解:
列表得:
过点(0,-2)和(1,1)画出直线l1,
再过点(0,2)和(1,1)画出直线l2,如图,
x 0 1
y=3x-2 -2 1
y=2-x 2 1
典例分析
由图象知:两条直线交点的坐标为(1,1),
∴方程组的解为:
典例分析
归 纳
用图象法解二元一次方程组的基本方法:
(1)将方程组中的两个方程转化成一次函数y=kx+b
的形式;
(2)在同一直角坐标系中画出两函数的图象;
(3)利用图象的直观性确定交点坐标.
自主学习
1.
【中考·巴中】已知二元一次方程组
的解为 则在同一平面直角坐标系中,直线 l1:y=x+5与直线 l2:y=- x-1的交点坐标为___________.
(-4,1)
课堂练习
2.
【中考·贵阳】若直线y=-x+a与直线y=x+b的交点坐标为(2,8),则a-b的值为( )
A.2 B.4
C.6 D.8
B
课堂练习
3.
在同一平面直角坐标系内画出二元一次方程2x-y-2=0和x-y+3=0所对应的一次函数的图象.利用图象求:
(1)方程2x-2=x+3的解;
(2)方程组 的解.
课堂练习
解:
画出y=2x-2和y=x+3的图象,如图所示.
(1)根据图象可知方程2x-2=x+3的解为x=5.
(2)根据图象可知方程组
的解
为
课堂练习
一次函数与二元
一次方程(组)
二元一次方程组无解 一次函数的图象平行(无交点);
二元一次方程组有一组解 一次函数的图象相交(有
一个交点);
二元一次方程组有无数个解 一次函数的图象重合
(有无数个交点).
课堂小结
https://www.21cnjy.com/help/help_extract.php
人教版八下数学
精品同步教学课件
19.2.3 一次函数
第2课时 一次函数与二元一次方程(组)
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
如图所示,是某次100米训练赛中飞人博尔特与
队友所跑的路程s(米)和所用时间t(秒)的函数图象.
观察图象,你能获取哪些信息
新知引入
一次函数与二元一次方程(组)的关系
1
二元一次方程与一次函数的联系
(1)任意一个二元一次方程都可化成y=kx+b的形式,
即令每个二元一次方程都对应一个一次函数,也
对应一条直线.
(2)直线y=kx+b上每一点的坐标均为这个二元一次
方程的解.
自主学习
例 1
如图所示的四条直线,其中直线上每个点的坐标都是
二元一次方程x-2y=2的解的是( )
C
典例分析
导引:
对于二元一次方程x-2y=2,当x=0时,y=-1;
当y=0时,x=2,故直线x-2y=2与两坐标轴的交点是
(0,-1),(2,0),对照四个选项中的直线,可知选C.
典例分析
归 纳
直线y=kx+b与x轴的交点的横坐标即是二元一
次方程y=kx+b中,当y=0时x的值;
直线y=kx+b与y轴的交点的纵坐标即是二元一
次方程y=kx+b中,当x=0时y的值.
解这类题,常运用数形结合思想.
问题
1号探测气球从海拔5m处出发,以1m/min的速度
上升.与此同时,2号探测气球从海拔15 m处出发,以
0.5 m/min的速度上升.两个气球都上升了1 h.
(1)用式子分别表示两个气球所在位置的海拔y (单位:m)
关于上升时间x(单位:min)的函数关系;
(2)在某时刻两个气球能否位于同一高度?如果能,这
时气球上升了多长时间?位于什么高度?
自主学习
(1)气球上升时间x满足0≤x≤60.
对于1号气球,y关于x的函数解析式为y=x+5.
对于2号气球,y关于x的函数解析式为y=0.5x+15.
(2)在某时刻两个气球位于同一高度,就是说对于x的某个值 (0≤x≤60),函数y=x+5和y=0.5x+15有相同的值y.如能求出这个x和y,则问题得到解决.由此容易想到解二元一次方程组
这就是说,当上升20 min时,两个气球都位于海拔25 m的高度.
分析:
自主学习
我们也可以用一次函数的图
象解释上述问题 的解答.如图,在
同一直角坐标系中,画出一次函
数y=x+5和y=0.5x+15的图象.
这两条直线的交点坐标为(20, 25),
这也说明当上升20 min时,两个
气球都位于海拔25 m的高度.
自主学习
一般地,因为每个含有未知数x和y的二元一次方程,
都可以改写为y=kx+b(k、b是常数,k≠0)的形式,所以每个这样的方程都对应一个一次函数,于是也对应一条直线.
这条直线上每个点的坐标(x,y)都是这个二元一次方程的解.
自主学习
由上可知,由含有未知数x和y的两个二元一次
方程组成的每个二元一 次方程组,都对应两个一次
函数,于是也对应两条直线.从“数”的角度看, 解
这样的方程组,相当于求自变量为何值时相应的两
个函数值相等,以及这个函数值是多少;从“形”
的角度看,解这样的方程组,相当于确定两条相应
直线交点的坐标.因此,我们可以用画一次函数图象
的方法得到方程组的解.
自主学习
二元一次方程组与一次函数的关系:
(1)二元一次方程组中的每个方程均可看作函数解析式.
(2)求二元一次方程组的解可看作求两个一次函数的交
点坐标.
自主学习
例2
利用图象法解二元一次方程组:
解:
列表得:
过点(0,-2)和(1,1)画出直线l1,
再过点(0,2)和(1,1)画出直线l2,如图,
x 0 1
y=3x-2 -2 1
y=2-x 2 1
典例分析
由图象知:两条直线交点的坐标为(1,1),
∴方程组的解为:
典例分析
归 纳
用图象法解二元一次方程组的基本方法:
(1)将方程组中的两个方程转化成一次函数y=kx+b
的形式;
(2)在同一直角坐标系中画出两函数的图象;
(3)利用图象的直观性确定交点坐标.
自主学习
1.
【中考·巴中】已知二元一次方程组
的解为 则在同一平面直角坐标系中,直线 l1:y=x+5与直线 l2:y=- x-1的交点坐标为___________.
(-4,1)
课堂练习
2.
【中考·贵阳】若直线y=-x+a与直线y=x+b的交点坐标为(2,8),则a-b的值为( )
A.2 B.4
C.6 D.8
B
课堂练习
3.
在同一平面直角坐标系内画出二元一次方程2x-y-2=0和x-y+3=0所对应的一次函数的图象.利用图象求:
(1)方程2x-2=x+3的解;
(2)方程组 的解.
课堂练习
解:
画出y=2x-2和y=x+3的图象,如图所示.
(1)根据图象可知方程2x-2=x+3的解为x=5.
(2)根据图象可知方程组
的解
为
课堂练习
一次函数与二元
一次方程(组)
二元一次方程组无解 一次函数的图象平行(无交点);
二元一次方程组有一组解 一次函数的图象相交(有
一个交点);
二元一次方程组有无数个解 一次函数的图象重合
(有无数个交点).
课堂小结
https://www.21cnjy.com/help/help_extract.php
