第16章 分式复习
图片预览


文档简介
分 式
知识要点及难点:
1 理解分式定义及基本性质。
2 理解分式有意义与值为0的条件。(难点)
3 会化简和通分。(难点)
4 能进行分式加减乘除运算,关键是通分和因式分解。
5. 有理式。
6. 能熟练解出分式方程。
一、分式的定义(概念)及基本性质
1、定义:设A、B表示两个整式,如果B中含有字母,式子就叫做分式,(B≠0)。
2、意义:整式的另一种表示法。
3、有意义的条件:B≠0;
无意义的条件:B=0;
值为零的条件:B≠0且A=0。
必须在有意义的条件下,才能谈分式的值。
4、最简分式:分子与分母没有公因式的分式叫最简分式。否则约分化简。
5、基本性质:同乘同除一个不为零的整式,值不变
==(M为不等于零的整式)。
二、分式的四则运算规则
运算规则与整式类似
1、加减:
2、乘除:,。
三、有理式的概念
有理式包括整式和分式。整式和分式统称有理式。
四、有关分式加减运算的技巧
1、通分
(1)加减的实质:分式加减运算就是通分。
(2)通分的依据:分式的基本性质(注意同乘的因式不能为零)。
(3)通分的关键:确定最简公分母(不是最简也可运算,但结果要化简)。
(4)最简公分母:各分母所有因式(包括因数)的最高次幂的积叫最简公分母。多项式应先分解因式。如何求?系数取最小公倍数;凡出现的以字母为底的幂的因式都要取;相同字母的幂的因式取最高次幂;这些因式的积就是最简公分母。
(5)通分结果中,分母不展开而写成连乘积的形式,分子则乘出来写成多项式,为进一步运算作准备。
2、分式通分的方法:
注意观察,如果不加思考地一味寻找公分母,有时会让计算变得更加复杂化。
(1)整体处理后通分。就是把分散的整式合并后,把整式的分母看分1,再寻找公共的最简公分母,再通分。
例3:
例4:
(2)化积约分后通分。先分解因式,再通分。
例5:
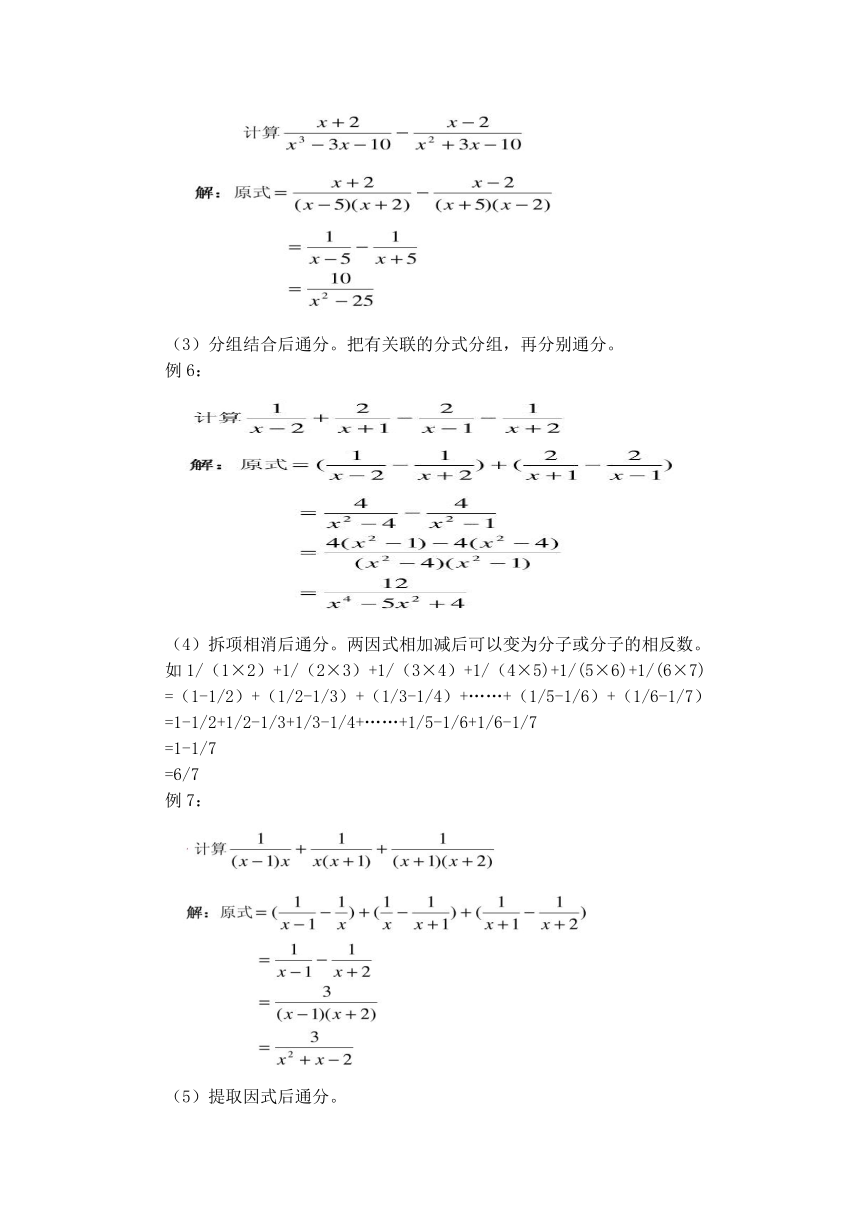
(3)分组结合后通分。把有关联的分式分组,再分别通分。
例6:
(4)拆项相消后通分。两因式相加减后可以变为分子或分子的相反数。
如1/(1×2)+1/(2×3)+1/(3×4)+1/(4×5)+1/(5×6)+1/(6×7)
=(1-1/2)+(1/2-1/3)+(1/3-1/4)+……+(1/5-1/6)+(1/6-1/7)
=1-1/2+1/2-1/3+1/3-1/4+……+1/5-1/6+1/6-1/7
=1-1/7
=6/7
例7:
(5)提取因式后通分。
例8:
(6)添项后通分。添一项或几项,使分式在巧合中简化
例9:
例10:
(7)拆项后通分。即是整体处理后通分的逆运算,通过拆项,消掉每对相反数。
例11:
(8)分离整式后通分。即把分子先简化,其实也是一种拆分。
例12:
(9)代入条件后通分。
例13:
(10)换元后通分。
例14:
五、分式的乘除运算
1、乘除规则:,
2、分式的乘除就是约分。
(1)乘除的实质:分式的乘除就是约分。
(2)约分的依据:分式的基本性质。(与通分不同,约分不必考虑约去的因式是否为零,但乘上的因式还需要考虑是否为零)
(3)约分的关键:先分解因式,然后找出分子分母的最大公因式。
(4)最简分式:一个分式的分子分母没有除1之外的公因式,叫最简分式。约分就是将分式化为最简分式的过程。
3、变号规则:分式的分子、分母和本身的符号,同时改变其中两个,其值不变。
4、分式的乘方
分式的乘方等于分子分母各自乘方,实质是几个相同的分式之积。
六、分式方程
1、概念:分母里含有字母的方程叫做分式方程。分式方程是方程中的一种。
2、特征:(1)含分母;(2)分母里含未知数。
3、可化为一元一次方程的分式方程的解法。
(1)去分母。方程两边同时乘以最简公分母,将分式方程化为整式方程;每一项都要乘,特别是以一个数或一个整式为一项时,这一项不能漏乘;若分式的符号是“-”,去掉分母后,分子应加括号;若遇到互为相反数时,不要忘了改变符号;
(2)按解整式方程的步骤求出未知数的值;
(3)验根(求出未知数的值后必须验根,因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根)。
验根时把整式方程的根代入最简公分母,如果最简公分母等于0,这个根就是增根。否则这个根就是原分式方程的根。若解出的根都是增根,则原方程无解。
在列分式方程解应用题时,不仅要检验所有的解是否满足方程式,还要检验是否符合题意。
知识要点及难点:
1 理解分式定义及基本性质。
2 理解分式有意义与值为0的条件。(难点)
3 会化简和通分。(难点)
4 能进行分式加减乘除运算,关键是通分和因式分解。
5. 有理式。
6. 能熟练解出分式方程。
一、分式的定义(概念)及基本性质
1、定义:设A、B表示两个整式,如果B中含有字母,式子就叫做分式,(B≠0)。
2、意义:整式的另一种表示法。
3、有意义的条件:B≠0;
无意义的条件:B=0;
值为零的条件:B≠0且A=0。
必须在有意义的条件下,才能谈分式的值。
4、最简分式:分子与分母没有公因式的分式叫最简分式。否则约分化简。
5、基本性质:同乘同除一个不为零的整式,值不变
==(M为不等于零的整式)。
二、分式的四则运算规则
运算规则与整式类似
1、加减:
2、乘除:,。
三、有理式的概念
有理式包括整式和分式。整式和分式统称有理式。
四、有关分式加减运算的技巧
1、通分
(1)加减的实质:分式加减运算就是通分。
(2)通分的依据:分式的基本性质(注意同乘的因式不能为零)。
(3)通分的关键:确定最简公分母(不是最简也可运算,但结果要化简)。
(4)最简公分母:各分母所有因式(包括因数)的最高次幂的积叫最简公分母。多项式应先分解因式。如何求?系数取最小公倍数;凡出现的以字母为底的幂的因式都要取;相同字母的幂的因式取最高次幂;这些因式的积就是最简公分母。
(5)通分结果中,分母不展开而写成连乘积的形式,分子则乘出来写成多项式,为进一步运算作准备。
2、分式通分的方法:
注意观察,如果不加思考地一味寻找公分母,有时会让计算变得更加复杂化。
(1)整体处理后通分。就是把分散的整式合并后,把整式的分母看分1,再寻找公共的最简公分母,再通分。
例3:
例4:
(2)化积约分后通分。先分解因式,再通分。
例5:
(3)分组结合后通分。把有关联的分式分组,再分别通分。
例6:
(4)拆项相消后通分。两因式相加减后可以变为分子或分子的相反数。
如1/(1×2)+1/(2×3)+1/(3×4)+1/(4×5)+1/(5×6)+1/(6×7)
=(1-1/2)+(1/2-1/3)+(1/3-1/4)+……+(1/5-1/6)+(1/6-1/7)
=1-1/2+1/2-1/3+1/3-1/4+……+1/5-1/6+1/6-1/7
=1-1/7
=6/7
例7:
(5)提取因式后通分。
例8:
(6)添项后通分。添一项或几项,使分式在巧合中简化
例9:
例10:
(7)拆项后通分。即是整体处理后通分的逆运算,通过拆项,消掉每对相反数。
例11:
(8)分离整式后通分。即把分子先简化,其实也是一种拆分。
例12:
(9)代入条件后通分。
例13:
(10)换元后通分。
例14:
五、分式的乘除运算
1、乘除规则:,
2、分式的乘除就是约分。
(1)乘除的实质:分式的乘除就是约分。
(2)约分的依据:分式的基本性质。(与通分不同,约分不必考虑约去的因式是否为零,但乘上的因式还需要考虑是否为零)
(3)约分的关键:先分解因式,然后找出分子分母的最大公因式。
(4)最简分式:一个分式的分子分母没有除1之外的公因式,叫最简分式。约分就是将分式化为最简分式的过程。
3、变号规则:分式的分子、分母和本身的符号,同时改变其中两个,其值不变。
4、分式的乘方
分式的乘方等于分子分母各自乘方,实质是几个相同的分式之积。
六、分式方程
1、概念:分母里含有字母的方程叫做分式方程。分式方程是方程中的一种。
2、特征:(1)含分母;(2)分母里含未知数。
3、可化为一元一次方程的分式方程的解法。
(1)去分母。方程两边同时乘以最简公分母,将分式方程化为整式方程;每一项都要乘,特别是以一个数或一个整式为一项时,这一项不能漏乘;若分式的符号是“-”,去掉分母后,分子应加括号;若遇到互为相反数时,不要忘了改变符号;
(2)按解整式方程的步骤求出未知数的值;
(3)验根(求出未知数的值后必须验根,因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根)。
验根时把整式方程的根代入最简公分母,如果最简公分母等于0,这个根就是增根。否则这个根就是原分式方程的根。若解出的根都是增根,则原方程无解。
在列分式方程解应用题时,不仅要检验所有的解是否满足方程式,还要检验是否符合题意。
