第9讲 二项分布与超几何分布(原卷版Word无答案)
文档属性
| 名称 | 第9讲 二项分布与超几何分布(原卷版Word无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 446.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 00:00:00 | ||
图片预览




文档简介
本资料分享自高中数学同步资源大全QQ群483122854 专注收集同步资源期待你的加入与分享
第9讲 二项分布与超几何分布
知识点一 n重伯努利试验及其特征
1.n重伯努利试验的概念
将一个伯努利试验独立地重复进行n次所组成的随机试验称为n重伯努利试验.
2.n重伯努利试验的共同特征
(1)同一个伯努利试验重复做n次.
(2)各次试验的结果相互独立.
知识点二 二项分布
一般地,在n重伯努利试验中,设每次试验中事件A发生的概率为p(0称随机变量X服从二项分布,记作X~B(n,p).
知识点三 二项分布的均值与方差
若X~B(n,p),则E(X)=np,D(X)=np(1-p).
知识点四 超几何分布
1.定义:一般地,假设一批产品共有N件,其中有M件次品,从N件产品中随机抽取n件(不放回),用X表示抽取的n件产品中的次品数,则X的分布列为
P(X=k)=,k=m,m+1,m+2,…,r.
其中n,N,M∈N*,M≤N,n≤N,m=max{0,n-N+M},r=min{n,M}.
如果随机变量X的分布列具有上式的形式,那么称随机变量X服从超几何分布.
2.均值:E(X)=.
【题型归纳】
考点一 超几何与二项分布概念的辨析
【例1-1】(2021·全国·高二课时练习)下列随机变量中,服从超几何分布的有________.(填序号)
①在10件产品中有3件次品,一件一件地不放回地任意取出4件,记取到的次品数为X;
②从3台甲型彩电和2台乙型彩电中任取2台,记X表示所取的2台彩电中甲型彩电的台数;
③一名学生骑自行车上学,途中有6个交通岗,记此学生遇到红灯数为随机变量X.
【例1-2】(2021·全国全国·)下列例子中随机变量ξ服从二项分布的有________.
①随机变量ξ表示重复抛掷一枚骰子n次中出现点数是3的倍数的次数;
②某射手击中目标的概率为0.9,从开始射击到击中目标所需的射击次数ξ;
③有一批产品共有N件,其中M件为次品,采用有放回抽取方法,ξ表示n次抽取中出现次品的件数(M④有一批产品共有N件,其中M件为次品,采用不放回抽取方法,ξ表示n次抽取中出现次品的件数.
【考点精练】
1.(2021·全国·高二课时练习)一个袋中有6个同样大小的黑球,编号为1,2,3,4,5,6,还有4个同样大小的白球,编号为7,8,9,10.现从中任取4个球,有如下几种变量:
①X表示取出的最大号码;
②X表示取出的最小号码;
③取出一个黑球记2分,取出一个白球记1分,X表示取出的4个球的总得分;
④X表示取出的黑球个数.
这四种变量中服从超几何分布的是( )
A.①② B.③④ C.①②④ D.①②③④
2.(2021·全国·高二课时练习)下列随机事件中的随机变量服从超几何分布的是( )
A.将一枚硬币连抛3次,记正面向上的次数为
B.从7男3女共10名学生干部中随机选出5名学生干部,记选出女生的人数为
C.某射手的射击命中率为0.8,现对目标射击1次,记命中的次数为
D.盒中有4个白球和3个黑球,每次从中摸出1个球且不放回,记第一次摸出黑球时摸取的次数为
3.(2021·全国·高二课时练习)下列例子中随机变量服从二项分布的个数为( )
①某同学投篮的命中率为0.6,他10次投篮中命中的次数;
②某射手击中目标的概率为0.9,从开始射击到击中目标所需的射击次数;
③从装有5个红球,5个白球的袋中,有放回地摸球,直到摸出白球为止,摸到白球时的摸球次数;
④有一批产品共有件,其中件为次品,采用不放回抽取方法,表示次抽取中出现次品的件数
A.0 B.1 C.2 D.3
4.(2021·全国·)下列选项中的随机变量不服从两点分布的是( )
A.抛掷一枚骰子,所得点数
B.某射击手射击一次,击中目标的次数
C.从装有除颜色外其余均相同的5个红球,3个白球的袋中任取1个球,设
D.某医生做一次手术,手术成功的次数
考点二 二项分布的均值与方差
【例2】.(2021·山东·高三月考)已知随机变量满足,且,则分别是( )
A.5,3 B.5,6 C.8,3 D.8,6
【考点精练】
1.(2021·江苏启东·高二期中)设随机变量X,Y满足:Y=3X﹣1,X~B,则V(Y)=()
A.4 B.5 C.6 D.7
2.(2021·全国·高二课时练习)设随机变量,若,则的值为( )
A. B. C. D.
3.(2021·山东威海·高二期末)已知随机变量,随机变量,则( )
A. B.
C. D.
考点三 二项分布
【例3】(2021·吉林·长春外国语学校高三期中(理))很多新手拿到驾驶证后开车上路,如果不遵守交通规则,将会面临扣分的处罚,为让广大新手了解驾驶证扣分新规定,某市交警部门结合机动车驾驶人有违法行为一次记12分 6分 3分 2分的新规定设置了一份试卷(满分100分),发放给新手解答,从中随机抽取了12名新手的成绩,成绩以茎叶图表示如图所示,并规定成绩低于95分的为不合格,需要加强学习,成绩不低于95分的为合格.
(1)求这12名新手的平均成绩与方差;
(2)将频率视为概率,根据样本估计总体的思想,若从该市新手中任选4名参加座谈会,用X表示成绩合格的人数,求X的分布列与数学期望.
【考点精练】
1.(2021·全国·高二课时练习)影响青少年近视形成的因素有遗传因素和环境因素,主要原因是环境因素.学生长时期近距离的用眼状态,加上不注意用眼卫生、不合理的作息时间很容易引起近视除了学习,学生平时爱看电视、上网玩电子游戏、不喜欢参加户外体育活动,都是造成近视情况日益严重的原因.为了解情况,现从某地区随机抽取16名学生,调查人员用对数视力表检查得到这16名学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶),如图.
(1)写出这组数据的众数和中位数.
(2)若视力测试结果不低于5.0,则称为“好视力”.
①从这16名学生中随机选取3名,求至少有2名学生是“好视力”的概率;
②以这16名学生中是“好视力”的频率代替该地区学生中是“好视力”的概率.若从该地区学生(人数较多)中任选3名,记表示抽到“好视力”学生的人数,求的分布列.
2.(2021·全国·高二课时练习)甲 乙二人进行定点投篮比赛,已知甲 乙二人每次投进的概率均为,两人各投1次称为一轮投篮.
(1)求乙在前3次投篮中,恰好投进2个球的概率;
(2)设前3轮投篮中,甲与乙进球个数差的绝对值为随机变量,求的分布列与期望.
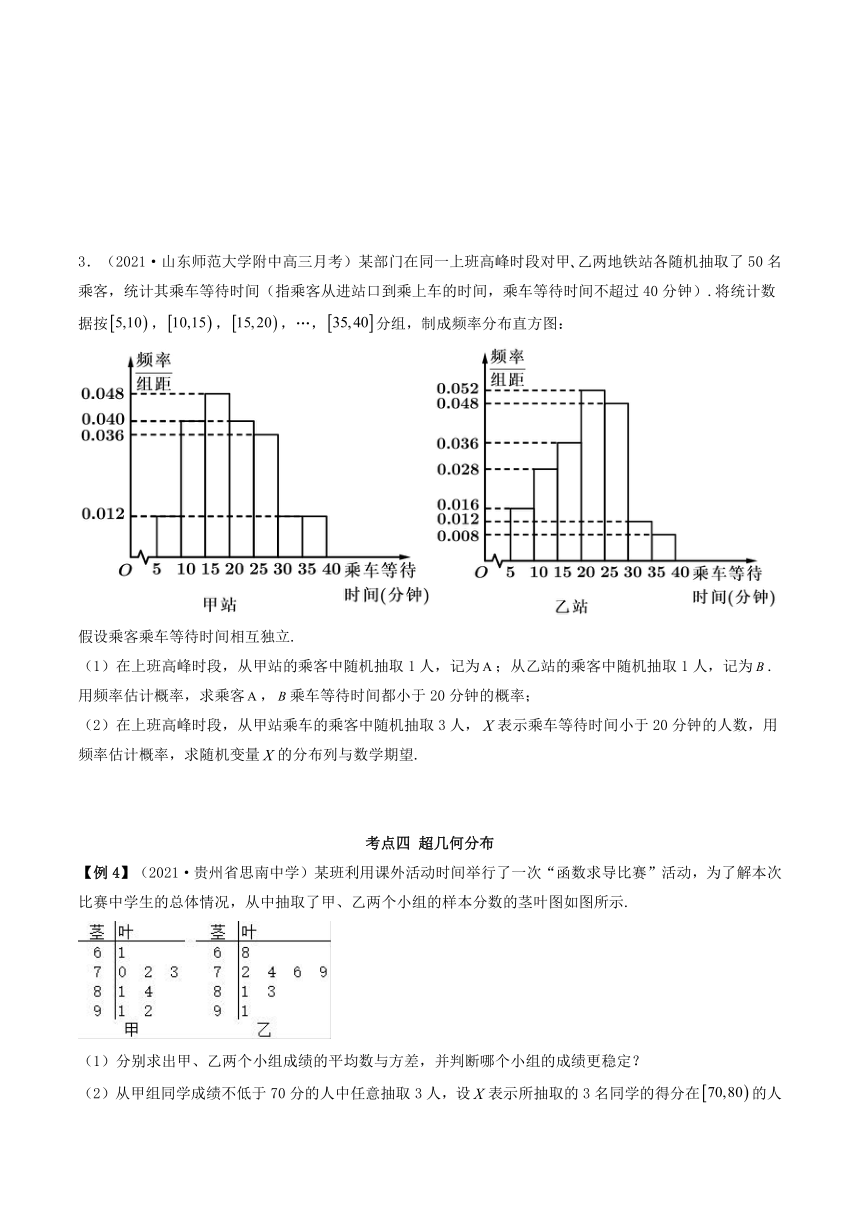
3.(2021·山东师范大学附中高三月考)某部门在同一上班高峰时段对甲 乙两地铁站各随机抽取了50名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,乘车等待时间不超过40分钟).将统计数据按,,,…,分组,制成频率分布直方图:
假设乘客乘车等待时间相互独立.
(1)在上班高峰时段,从甲站的乘客中随机抽取1人,记为;从乙站的乘客中随机抽取1人,记为.用频率估计概率,求乘客,乘车等待时间都小于20分钟的概率;
(2)在上班高峰时段,从甲站乘车的乘客中随机抽取3人,表示乘车等待时间小于20分钟的人数,用频率估计概率,求随机变量的分布列与数学期望.
考点四 超几何分布
【例4】(2021·贵州省思南中学)某班利用课外活动时间举行了一次“函数求导比赛”活动,为了解本次比赛中学生的总体情况,从中抽取了甲、乙两个小组的样本分数的茎叶图如图所示.
(1)分别求出甲、乙两个小组成绩的平均数与方差,并判断哪个小组的成绩更稳定?
(2)从甲组同学成绩不低于70分的人中任意抽取3人,设表示所抽取的3名同学的得分在的人数,求的分布列及数学期望.
【考点精练】
1.(2021·安徽·六安一中)2020年5月28日,十三届全国人大三次会议表决通过了《中华人民共和国民法典》,自2021年1月1日起施行.它被称为“社会生活的百科全书”,是新中国第一部以法典命名的法律,在法律体系中居于基础性地位,也是市场经济的基本法某中学培养学生知法懂法,组织全校学生学习《中华人民共和国民法典》并组织知识竞赛.为了解学习的效果,现从高一,高二两个年级中各随机抽取20名学生的成绩(单位:分),绘制成如图所示的茎叶图:
根据学生的竞赛成绩,将其分为四个等级:
测试成绩(单位:分)
等级 合格 中等 良好 优秀
(1)从样本中任取2名同学的竞赛成绩,在成绩为优秀的情况下,求这2名同学来自同一个年级的概率;
(2)现从样本中成绩为良好的学生中随机抽取3人座谈,记为抽到高二年级的人数,求的分布列,数学期望与方差.
2.(2021·广西柳州)为庆祝2021年中国共产党成立100周年,某校高二年级举行“党史知识你我答”活动,共有10个班,每班选5名选手参加了预赛,预赛满分为150分,现预赛成绩全部介于90分到140分之间.将成绩结果按如下方式分成五组:第一组,第二组,…,第五组.按上述分组方法得到的频率分布直方图如图所示.
(1)若成绩大于或等于100分且小于120分认为是良好的,求参赛学生在这次活动中成绩良好的人数;
(2)若从第一 五组中共随机取出两个成绩,记X为取得第一组成绩的个数,求X的分布列与数学期望.
3.(2021·江苏赣榆·高二期中)已知袋中装有5个白球,2个黑球,3个红球,现从中任取3个球.
(1)求恰有一个白球的方法种数;
(2)求至少有一个红球的方法种数;
(3)设随机变量X为取出3球中黑球的个数,求X的概率分布及数学期望.
考点五 二项分布与超几何分布的综合
【例5】(2021·全国·高二课时练习)袋中有6个白球、3个黑球,从中随机地连续抽取2次,每次取1个球.
(1)若每次抽取后都放回,设取到黑球的次数为X,求X的分布列;
(2)若每次抽取后都不放回,设取到黑球的个数为Y,求Y的分布列.
【考点精练】
1.(2021·全国·高二课时练习)某校从高三年级中选拔一个班级代表学校参加“学习强国知识大赛”,经过层层选拔,甲、乙两个班级进入最后决赛,规定回答1道相关问题做最后的评判选择由哪个班级代表学校参加大赛.每个班级4名选手,现从每个班级4名选手中随机抽取2人回答这个问题.已知这4人中,甲班级有3人可以正确回答这道题目,而乙班级4人中能正确回答这道题目的概率均为,甲、乙两班级每个人对问题的回答都是相互独立、互不影响的.
(1)求甲、乙两个班级抽取的4人都能正确回答的概率.
(2)设甲、乙两个班级被抽取的选手中能正确回答题目的人数分别为,,求随机变量,的期望,和方差,,并由此分析由哪个班级代表学校参加大赛更好.
2.(2021·全国·高二单元测试)是指大气中直径小于或等于的颗粒物,也称为可入肺颗粒物,我国标准采用世卫组织设定的最宽限值,即日均值在以下空气质量为一级;在之间空气质量为二级;在以上空气质量为污染.某市生态环境局从该市年上半年每天的监测数据中随机抽取天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
(1)从这天的数据中任取天,求这天空气质量达到一级的概率;
(2)从这天的数据中任取天的数据,记表示其中空气质量达到一级的天数,求的分布列和数学期望;
(3)以这天的的日均值来估计一年的空气质量情况(一年按天来计算),则一年中大约有多少天的空气质量达到一级?
3.(2021·全国·高二课时练习)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的质量(单位:克),质量的分组区间为(490,495],(495,500],…,(510,515].由此得到样本的频率分布直方图如图.
(1)根据频率分布直方图,求质量超过505克的产品数量;
(2)在上述抽取的40件产品中任取2件,设X为质量超过505克的产品数量,求X的分布列;
(3)从该流水线上任取2件产品,设Y为质量超过505克的产品数量,求Y的分布列.
考点六 二项分布与超几何分布与其他知识综合
【例6】(2021·山东威海·高二期末)某企业为检验某种设备生产的零件质量,现随机选取个零件进行检验,分出合格品和次品.设每个零件是次品的概率为,且相互独立.
(Ⅰ)若个零件中恰有2个次品的概率为,求的最大值点;
(Ⅱ)若合格品又分为一等品和二等品,每个零件是二等品的概率为是一等品概率的倍. 已知生产一个一等品可获利元,生产一个二等品可获利元,生产一个次品会亏损元,当每个零件平均获利低于元时,需对设备进行技术升级. 当满足什么条件时,企业需对该设备进行技术升级?
【考点精练】
1.(2021·辽宁·大连二十四中高二期中)某商城玩具柜台五一期间促销,购买甲、乙系列的盲盒,并且集齐所有的产品就可以赠送节日送礼,现有甲、乙两个系列盲盒,每个甲系列盲盒可以开出玩偶,,中的一个,每个乙系列盲盒可以开出玩偶,中的一个.
(1)记事件:一次性购买个甲系列盲盒后集齐玩偶,,玩偶;事件:一次性购买个乙系列盲盒后集齐,玩偶;求概率及;
(2)某礼品店限量出售甲、乙两个系列的盲盒,每个消费者每天只有一次购买机会,且购买时,只能选择其中一个系列的一个盲盒.通过统计发现:第一次购买盲盒的消费者购买甲系列的概率为,购买乙系列的概率为;而前一次购买甲系列的消费者下一次购买甲系列的概率为,购买乙系列的概率为,前一次购买乙系列的消费者下一次购买甲系列的概率为,购买乙系列的概率为;如此往复,记某人第次购买甲系列的概率为.
①求的通项公式;
②若每天购买盲盒的人数约为,且这人都已购买过很多次这两个系列的盲盒,试估计该礼品店每天应准备甲、乙两个系列的盲盒各多少个.
2.(2021·山东·济宁一中 )由于“新冠肺炎”对抵抗力差的人的感染率相对更高,特别是老年人群体,因此某社区在疫情控制后,及时给老年人免费体检,通过体检发现“高血糖,高血脂,高血压”,即“三高”老人较多.为此社区根据医生的建议为每位老人提供了一份详细的健康安排表,还特地建设了一个老年人活动中心,老年人每天可以到该活动中心去活动,以增强体质,通过统计每周到活动中心去运动的老年人的活动时间,得到了以下频率分布直方图.
(1)从到活动中心参加活动的老人中任意选取5人.
①若将频率视为概率,求至少有3人每周活动时间在[8,9)(单位:)的概率;
②若抽取的5人中每周活动时间在[8,11](单位:)的人数为2人,从5人中选出3人进行健康情况调查,记3人中每周活动时间在[8,11](单位:h)的人数为ξ,求ξ的分布列和期望;
(2)将某人的每周活动时间量与所有老人的每周平均活动时间量比较,当超出所有老人的每周平均活动量不少于0.74时,则称该老人为“活动爱好者”,从参加活动的老人中随机抽取10人,且抽到k人为“活动爱好者”的可能性最大,试求k的值.(每组数据以区间的中点值为代表)
3.(2021·江苏泰州·模拟预测)现有一批疫苗试剂,拟进入动物试验阶段,将1000只动物平均分成100组,任选一组进行试验.第一轮注射,对该组的每只动物都注射一次,若检验出该组中有9只或10只动物产生抗体,说明疫苗有效,试验终止;否则对没有产生抗体的动物进行第二轮注射,再次检验.如果被二次注射的动物都产生抗体,说明疫苗有效,否则需要改进疫苗.设每只动物是否产生抗体相互独立,两次注射疫苗互不影响,且产生抗体的概率均为.
(1)求该组试验只需第一轮注射的概率(用含的多项式表示);
(2)记该组动物需要注射次数的数学期望为,求证:
联系QQ309000116加入百度网盘群2500G一线老师必备资料一键转存,自动更新,一劳永逸
第9讲 二项分布与超几何分布
知识点一 n重伯努利试验及其特征
1.n重伯努利试验的概念
将一个伯努利试验独立地重复进行n次所组成的随机试验称为n重伯努利试验.
2.n重伯努利试验的共同特征
(1)同一个伯努利试验重复做n次.
(2)各次试验的结果相互独立.
知识点二 二项分布
一般地,在n重伯努利试验中,设每次试验中事件A发生的概率为p(0
知识点三 二项分布的均值与方差
若X~B(n,p),则E(X)=np,D(X)=np(1-p).
知识点四 超几何分布
1.定义:一般地,假设一批产品共有N件,其中有M件次品,从N件产品中随机抽取n件(不放回),用X表示抽取的n件产品中的次品数,则X的分布列为
P(X=k)=,k=m,m+1,m+2,…,r.
其中n,N,M∈N*,M≤N,n≤N,m=max{0,n-N+M},r=min{n,M}.
如果随机变量X的分布列具有上式的形式,那么称随机变量X服从超几何分布.
2.均值:E(X)=.
【题型归纳】
考点一 超几何与二项分布概念的辨析
【例1-1】(2021·全国·高二课时练习)下列随机变量中,服从超几何分布的有________.(填序号)
①在10件产品中有3件次品,一件一件地不放回地任意取出4件,记取到的次品数为X;
②从3台甲型彩电和2台乙型彩电中任取2台,记X表示所取的2台彩电中甲型彩电的台数;
③一名学生骑自行车上学,途中有6个交通岗,记此学生遇到红灯数为随机变量X.
【例1-2】(2021·全国全国·)下列例子中随机变量ξ服从二项分布的有________.
①随机变量ξ表示重复抛掷一枚骰子n次中出现点数是3的倍数的次数;
②某射手击中目标的概率为0.9,从开始射击到击中目标所需的射击次数ξ;
③有一批产品共有N件,其中M件为次品,采用有放回抽取方法,ξ表示n次抽取中出现次品的件数(M
【考点精练】
1.(2021·全国·高二课时练习)一个袋中有6个同样大小的黑球,编号为1,2,3,4,5,6,还有4个同样大小的白球,编号为7,8,9,10.现从中任取4个球,有如下几种变量:
①X表示取出的最大号码;
②X表示取出的最小号码;
③取出一个黑球记2分,取出一个白球记1分,X表示取出的4个球的总得分;
④X表示取出的黑球个数.
这四种变量中服从超几何分布的是( )
A.①② B.③④ C.①②④ D.①②③④
2.(2021·全国·高二课时练习)下列随机事件中的随机变量服从超几何分布的是( )
A.将一枚硬币连抛3次,记正面向上的次数为
B.从7男3女共10名学生干部中随机选出5名学生干部,记选出女生的人数为
C.某射手的射击命中率为0.8,现对目标射击1次,记命中的次数为
D.盒中有4个白球和3个黑球,每次从中摸出1个球且不放回,记第一次摸出黑球时摸取的次数为
3.(2021·全国·高二课时练习)下列例子中随机变量服从二项分布的个数为( )
①某同学投篮的命中率为0.6,他10次投篮中命中的次数;
②某射手击中目标的概率为0.9,从开始射击到击中目标所需的射击次数;
③从装有5个红球,5个白球的袋中,有放回地摸球,直到摸出白球为止,摸到白球时的摸球次数;
④有一批产品共有件,其中件为次品,采用不放回抽取方法,表示次抽取中出现次品的件数
A.0 B.1 C.2 D.3
4.(2021·全国·)下列选项中的随机变量不服从两点分布的是( )
A.抛掷一枚骰子,所得点数
B.某射击手射击一次,击中目标的次数
C.从装有除颜色外其余均相同的5个红球,3个白球的袋中任取1个球,设
D.某医生做一次手术,手术成功的次数
考点二 二项分布的均值与方差
【例2】.(2021·山东·高三月考)已知随机变量满足,且,则分别是( )
A.5,3 B.5,6 C.8,3 D.8,6
【考点精练】
1.(2021·江苏启东·高二期中)设随机变量X,Y满足:Y=3X﹣1,X~B,则V(Y)=()
A.4 B.5 C.6 D.7
2.(2021·全国·高二课时练习)设随机变量,若,则的值为( )
A. B. C. D.
3.(2021·山东威海·高二期末)已知随机变量,随机变量,则( )
A. B.
C. D.
考点三 二项分布
【例3】(2021·吉林·长春外国语学校高三期中(理))很多新手拿到驾驶证后开车上路,如果不遵守交通规则,将会面临扣分的处罚,为让广大新手了解驾驶证扣分新规定,某市交警部门结合机动车驾驶人有违法行为一次记12分 6分 3分 2分的新规定设置了一份试卷(满分100分),发放给新手解答,从中随机抽取了12名新手的成绩,成绩以茎叶图表示如图所示,并规定成绩低于95分的为不合格,需要加强学习,成绩不低于95分的为合格.
(1)求这12名新手的平均成绩与方差;
(2)将频率视为概率,根据样本估计总体的思想,若从该市新手中任选4名参加座谈会,用X表示成绩合格的人数,求X的分布列与数学期望.
【考点精练】
1.(2021·全国·高二课时练习)影响青少年近视形成的因素有遗传因素和环境因素,主要原因是环境因素.学生长时期近距离的用眼状态,加上不注意用眼卫生、不合理的作息时间很容易引起近视除了学习,学生平时爱看电视、上网玩电子游戏、不喜欢参加户外体育活动,都是造成近视情况日益严重的原因.为了解情况,现从某地区随机抽取16名学生,调查人员用对数视力表检查得到这16名学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶),如图.
(1)写出这组数据的众数和中位数.
(2)若视力测试结果不低于5.0,则称为“好视力”.
①从这16名学生中随机选取3名,求至少有2名学生是“好视力”的概率;
②以这16名学生中是“好视力”的频率代替该地区学生中是“好视力”的概率.若从该地区学生(人数较多)中任选3名,记表示抽到“好视力”学生的人数,求的分布列.
2.(2021·全国·高二课时练习)甲 乙二人进行定点投篮比赛,已知甲 乙二人每次投进的概率均为,两人各投1次称为一轮投篮.
(1)求乙在前3次投篮中,恰好投进2个球的概率;
(2)设前3轮投篮中,甲与乙进球个数差的绝对值为随机变量,求的分布列与期望.
3.(2021·山东师范大学附中高三月考)某部门在同一上班高峰时段对甲 乙两地铁站各随机抽取了50名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,乘车等待时间不超过40分钟).将统计数据按,,,…,分组,制成频率分布直方图:
假设乘客乘车等待时间相互独立.
(1)在上班高峰时段,从甲站的乘客中随机抽取1人,记为;从乙站的乘客中随机抽取1人,记为.用频率估计概率,求乘客,乘车等待时间都小于20分钟的概率;
(2)在上班高峰时段,从甲站乘车的乘客中随机抽取3人,表示乘车等待时间小于20分钟的人数,用频率估计概率,求随机变量的分布列与数学期望.
考点四 超几何分布
【例4】(2021·贵州省思南中学)某班利用课外活动时间举行了一次“函数求导比赛”活动,为了解本次比赛中学生的总体情况,从中抽取了甲、乙两个小组的样本分数的茎叶图如图所示.
(1)分别求出甲、乙两个小组成绩的平均数与方差,并判断哪个小组的成绩更稳定?
(2)从甲组同学成绩不低于70分的人中任意抽取3人,设表示所抽取的3名同学的得分在的人数,求的分布列及数学期望.
【考点精练】
1.(2021·安徽·六安一中)2020年5月28日,十三届全国人大三次会议表决通过了《中华人民共和国民法典》,自2021年1月1日起施行.它被称为“社会生活的百科全书”,是新中国第一部以法典命名的法律,在法律体系中居于基础性地位,也是市场经济的基本法某中学培养学生知法懂法,组织全校学生学习《中华人民共和国民法典》并组织知识竞赛.为了解学习的效果,现从高一,高二两个年级中各随机抽取20名学生的成绩(单位:分),绘制成如图所示的茎叶图:
根据学生的竞赛成绩,将其分为四个等级:
测试成绩(单位:分)
等级 合格 中等 良好 优秀
(1)从样本中任取2名同学的竞赛成绩,在成绩为优秀的情况下,求这2名同学来自同一个年级的概率;
(2)现从样本中成绩为良好的学生中随机抽取3人座谈,记为抽到高二年级的人数,求的分布列,数学期望与方差.
2.(2021·广西柳州)为庆祝2021年中国共产党成立100周年,某校高二年级举行“党史知识你我答”活动,共有10个班,每班选5名选手参加了预赛,预赛满分为150分,现预赛成绩全部介于90分到140分之间.将成绩结果按如下方式分成五组:第一组,第二组,…,第五组.按上述分组方法得到的频率分布直方图如图所示.
(1)若成绩大于或等于100分且小于120分认为是良好的,求参赛学生在这次活动中成绩良好的人数;
(2)若从第一 五组中共随机取出两个成绩,记X为取得第一组成绩的个数,求X的分布列与数学期望.
3.(2021·江苏赣榆·高二期中)已知袋中装有5个白球,2个黑球,3个红球,现从中任取3个球.
(1)求恰有一个白球的方法种数;
(2)求至少有一个红球的方法种数;
(3)设随机变量X为取出3球中黑球的个数,求X的概率分布及数学期望.
考点五 二项分布与超几何分布的综合
【例5】(2021·全国·高二课时练习)袋中有6个白球、3个黑球,从中随机地连续抽取2次,每次取1个球.
(1)若每次抽取后都放回,设取到黑球的次数为X,求X的分布列;
(2)若每次抽取后都不放回,设取到黑球的个数为Y,求Y的分布列.
【考点精练】
1.(2021·全国·高二课时练习)某校从高三年级中选拔一个班级代表学校参加“学习强国知识大赛”,经过层层选拔,甲、乙两个班级进入最后决赛,规定回答1道相关问题做最后的评判选择由哪个班级代表学校参加大赛.每个班级4名选手,现从每个班级4名选手中随机抽取2人回答这个问题.已知这4人中,甲班级有3人可以正确回答这道题目,而乙班级4人中能正确回答这道题目的概率均为,甲、乙两班级每个人对问题的回答都是相互独立、互不影响的.
(1)求甲、乙两个班级抽取的4人都能正确回答的概率.
(2)设甲、乙两个班级被抽取的选手中能正确回答题目的人数分别为,,求随机变量,的期望,和方差,,并由此分析由哪个班级代表学校参加大赛更好.
2.(2021·全国·高二单元测试)是指大气中直径小于或等于的颗粒物,也称为可入肺颗粒物,我国标准采用世卫组织设定的最宽限值,即日均值在以下空气质量为一级;在之间空气质量为二级;在以上空气质量为污染.某市生态环境局从该市年上半年每天的监测数据中随机抽取天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).
(1)从这天的数据中任取天,求这天空气质量达到一级的概率;
(2)从这天的数据中任取天的数据,记表示其中空气质量达到一级的天数,求的分布列和数学期望;
(3)以这天的的日均值来估计一年的空气质量情况(一年按天来计算),则一年中大约有多少天的空气质量达到一级?
3.(2021·全国·高二课时练习)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的质量(单位:克),质量的分组区间为(490,495],(495,500],…,(510,515].由此得到样本的频率分布直方图如图.
(1)根据频率分布直方图,求质量超过505克的产品数量;
(2)在上述抽取的40件产品中任取2件,设X为质量超过505克的产品数量,求X的分布列;
(3)从该流水线上任取2件产品,设Y为质量超过505克的产品数量,求Y的分布列.
考点六 二项分布与超几何分布与其他知识综合
【例6】(2021·山东威海·高二期末)某企业为检验某种设备生产的零件质量,现随机选取个零件进行检验,分出合格品和次品.设每个零件是次品的概率为,且相互独立.
(Ⅰ)若个零件中恰有2个次品的概率为,求的最大值点;
(Ⅱ)若合格品又分为一等品和二等品,每个零件是二等品的概率为是一等品概率的倍. 已知生产一个一等品可获利元,生产一个二等品可获利元,生产一个次品会亏损元,当每个零件平均获利低于元时,需对设备进行技术升级. 当满足什么条件时,企业需对该设备进行技术升级?
【考点精练】
1.(2021·辽宁·大连二十四中高二期中)某商城玩具柜台五一期间促销,购买甲、乙系列的盲盒,并且集齐所有的产品就可以赠送节日送礼,现有甲、乙两个系列盲盒,每个甲系列盲盒可以开出玩偶,,中的一个,每个乙系列盲盒可以开出玩偶,中的一个.
(1)记事件:一次性购买个甲系列盲盒后集齐玩偶,,玩偶;事件:一次性购买个乙系列盲盒后集齐,玩偶;求概率及;
(2)某礼品店限量出售甲、乙两个系列的盲盒,每个消费者每天只有一次购买机会,且购买时,只能选择其中一个系列的一个盲盒.通过统计发现:第一次购买盲盒的消费者购买甲系列的概率为,购买乙系列的概率为;而前一次购买甲系列的消费者下一次购买甲系列的概率为,购买乙系列的概率为,前一次购买乙系列的消费者下一次购买甲系列的概率为,购买乙系列的概率为;如此往复,记某人第次购买甲系列的概率为.
①求的通项公式;
②若每天购买盲盒的人数约为,且这人都已购买过很多次这两个系列的盲盒,试估计该礼品店每天应准备甲、乙两个系列的盲盒各多少个.
2.(2021·山东·济宁一中 )由于“新冠肺炎”对抵抗力差的人的感染率相对更高,特别是老年人群体,因此某社区在疫情控制后,及时给老年人免费体检,通过体检发现“高血糖,高血脂,高血压”,即“三高”老人较多.为此社区根据医生的建议为每位老人提供了一份详细的健康安排表,还特地建设了一个老年人活动中心,老年人每天可以到该活动中心去活动,以增强体质,通过统计每周到活动中心去运动的老年人的活动时间,得到了以下频率分布直方图.
(1)从到活动中心参加活动的老人中任意选取5人.
①若将频率视为概率,求至少有3人每周活动时间在[8,9)(单位:)的概率;
②若抽取的5人中每周活动时间在[8,11](单位:)的人数为2人,从5人中选出3人进行健康情况调查,记3人中每周活动时间在[8,11](单位:h)的人数为ξ,求ξ的分布列和期望;
(2)将某人的每周活动时间量与所有老人的每周平均活动时间量比较,当超出所有老人的每周平均活动量不少于0.74时,则称该老人为“活动爱好者”,从参加活动的老人中随机抽取10人,且抽到k人为“活动爱好者”的可能性最大,试求k的值.(每组数据以区间的中点值为代表)
3.(2021·江苏泰州·模拟预测)现有一批疫苗试剂,拟进入动物试验阶段,将1000只动物平均分成100组,任选一组进行试验.第一轮注射,对该组的每只动物都注射一次,若检验出该组中有9只或10只动物产生抗体,说明疫苗有效,试验终止;否则对没有产生抗体的动物进行第二轮注射,再次检验.如果被二次注射的动物都产生抗体,说明疫苗有效,否则需要改进疫苗.设每只动物是否产生抗体相互独立,两次注射疫苗互不影响,且产生抗体的概率均为.
(1)求该组试验只需第一轮注射的概率(用含的多项式表示);
(2)记该组动物需要注射次数的数学期望为,求证:
联系QQ309000116加入百度网盘群2500G一线老师必备资料一键转存,自动更新,一劳永逸
