第10讲 正态分布(原卷版Word无答案)
文档属性
| 名称 | 第10讲 正态分布(原卷版Word无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 592.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-30 22:23:46 | ||
图片预览




文档简介
本资料分享自高中数学同步资源大全QQ群483122854 专注收集同步资源期待你的加入与分享
第10讲 正态分布
【知识梳理】
知识点一 正态曲线与正态分布
1.我们称f(x)=,x∈R,其中μ∈R,σ>0为参数,为正态密度函数,称其图象为正态分布密度曲线,简称正态曲线.
2.若随机变量X的概率密度函数为f(x),则称随机变量X服从正态分布,记为X~N(μ,σ2).
特别地,当μ=0,σ=1时,称随机变量X服从标准正态分布.
3.若X~N(μ,σ2),如图所示,X取值不超过x的概率P(X≤x)为图中区域A的面积,而P(a≤X≤b)为区域B的面积.
知识点二 正态曲线的特点
1.对 x∈R,f(x)>0,它的图象在x轴的上方.
2.曲线与x轴之间的面积为1.
3.曲线是单峰的,它关于直线x=μ对称.
4.曲线在x=μ处达到峰值.
5.当|x|无限增大时,曲线无限接近x轴.
6.当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移,如图①.
7.当μ一定时,曲线的形状由σ确定,σ较小时曲线“瘦高”,表示随机变量X的分布比较集中;σ较大时,曲线“矮胖”,表示随机变量X的分布比较分散,如图②.
知识点三 正态总体在三个特殊区间内取值的概率值及3σ原则
P(μ-σ≤X≤μ+σ)≈0.682 7;
P(μ-2σ≤X≤μ+2σ)≈0.954 5;
P(μ-3σ≤X≤μ+3σ)≈0.997 3.
尽管正态变量的取值范围是(-∞,+∞),但在一次试验中,X的取值几乎总是落在区间[μ-3σ,μ+3σ]内,而在此区间以外取值的概率大约只有0.002 7,通常认为这种情况在一次试验中几乎不可能发生.
在实际应用中,通常认为服从于正态分布N(μ,σ2)的随机变量X只取[μ-3σ,μ+3σ]中的值,这在统计学中称为3σ原则.
【题型归纳】
考点一 正态分布曲线
【例1】(2021·黑龙江·哈尔滨三中高二月考)下列是关于正态曲线性质的说法:
①曲线关于直线对称,且恒位于轴上方;
②曲线关于直线对称,且仅当时才位于轴上方;
③曲线对应的正态密度函数是一个偶函数,因此曲线关于轴对称;
④曲线在处位于最高点,由这一点向左、右两边延伸时,曲线逐渐降低;
⑤曲线的位置由确定,曲线的形状由确定.
其中说法正确的是( )
A.①④⑤ B.②④⑤ C.③④⑤ D.①⑤
【考点精练】
1.(2021·全国·高二课时练习)(多选)甲、乙两类水果的质量(单位:kg)分别服从正态分布,,,其正态分布的密度曲线,,如图所示,则下列说法正确的是( )
A.甲类水果的平均质量
B.乙类水果的质量比甲类水果的质量更集中于均值左右
C.甲类水果的平均质量比乙类水果的平均质量小
D.乙类水果的质量服从的正态分布的参数
2.(2021·全国·高二课时练习)(多选)设X~N(μ1,),Y~N(μ2,),这两个正态分布密度曲线如图所示.下列结论中错误的是( )
A.P(Y≥μ2)≥P(Y≥μ1)
B.P(X≤σ2)≤P(X≤σ1)
C.对任意正数t,P(X≤t)>P(Y≤t)
D.对任意正数t,P(X>t)>P(Y>t)
3.(2021·全国·高二课时练习)(多选)下面给出的关于正态曲线的4个叙述中,正确的有( )
A.曲线在x轴上方,且与x轴不相交
B.当x>μ时,曲线下降,当x<μ时,曲线上升
C.当μ一定时,σ越小,总体分布越分散,σ越大,总体分布越集中
D.曲线关于直线x=μ对称,且当x=μ时,位于最高点
4.(2021·全国·高二课时练习)(多选)一次教学质量检测中,甲、乙、丙三科考试成绩的正态分布密度曲线如图所示,下列说法中不正确的是( )
A.甲科总体的标准差最小
B.丙科总体的平均数最小
C.乙科总体的标准差及平均数都比甲小,比丙大
D.甲、乙、丙总体的平均数不相同
考点二 正态分布(小题)
【例2-1】(2021·全国·高二课时练习)若随机变量,且,则等于( )
A.0.6 B.0.5
C.0.4 D.0.3
【例2-2】(2021·全国·高二课时练习)设随机变量的正态分布密度函数为,,则参数,的值分别是( )
A., B.,
C., D.,
【考点精练】
1.(2021·广东·广州市协和中学高二期中)若随机变量,且,则( )
A.0.6 B.0.5
C.0.4 D.0.3
2.(2021·全国·高二单元测试)某军工企业为某种型号的新式步枪生产了一批枪管,其口径误差(单位:微米)服从正态分布,从已经生产出的枪管中随机取出一只,则其口径误差在区间内的概率为( )
(注:若随机变量服从正态分布,则,)
A.31.7% B.27.18%
C.13. 55% D.4.5%
3.(2021·全国·高二课时练习)在某市2020年3月份的高三线上质量检测考试中,学生的数学成绩服从正态分布N(98,100).已知参加本次考试的全市学生有9 455人,如果某学生在这次考试中的数学成绩是108分,那么他的数学成绩大约排在全市第( )
A.1 500名 B.1 700名
C.4 500名 D.8 000名
4.(2021·全国·高二课时练习)随机变量服从正态分布N(1,4),若,则 ( )
A. B.
C. D.
考点三 正态分布的应用(解答题)
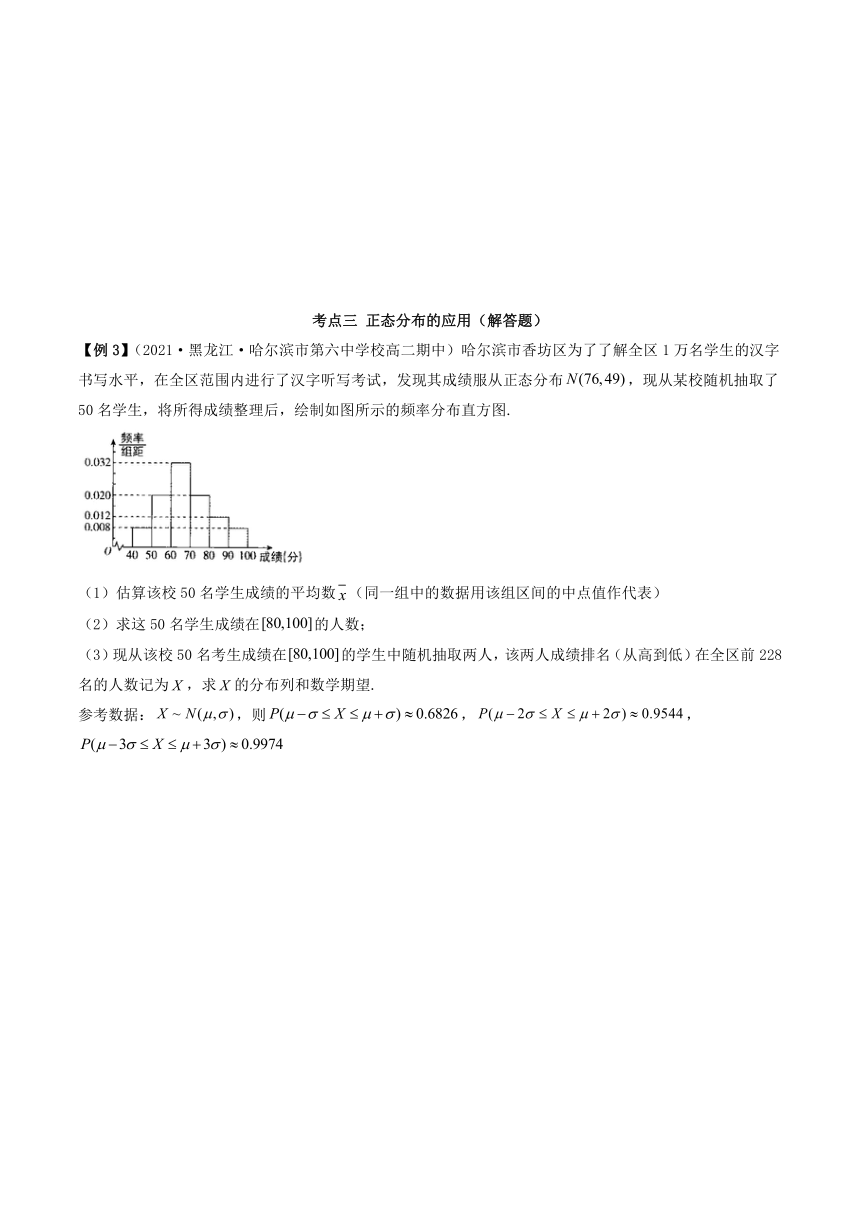
【例3】(2021·黑龙江·哈尔滨市第六中学校高二期中)哈尔滨市香坊区为了了解全区1万名学生的汉字书写水平,在全区范围内进行了汉字听写考试,发现其成绩服从正态分布,现从某校随机抽取了50名学生,将所得成绩整理后,绘制如图所示的频率分布直方图.
(1)估算该校50名学生成绩的平均数(同一组中的数据用该组区间的中点值作代表)
(2)求这50名学生成绩在的人数;
(3)现从该校50名考生成绩在的学生中随机抽取两人,该两人成绩排名(从高到低)在全区前228名的人数记为,求的分布列和数学期望.
参考数据:,则,,
【考点精练】
1(2021·全国·高二课时练习)某市在实施垃圾分类的过程中,从本市人口数量在两万人左右的A类社区(全市共320个)中随机抽取了50个进行调查,统计这50个社区某天产生的垃圾量(单位:吨),得到如下频数分布表,并将这一天垃圾数量超过8吨的社区定为“超标”社区.
垃圾量
频数 5 6 9 12 8 6 7
(1)估计该市类社区这一天垃圾量的平均值.
(2)若该市类社区这一天的垃圾量大致服从正态分布,其中近似为个样本社区的平均值(精确到0.1吨,估计该市类社区中“超标”社区的个数.
(3)根据原始样本数据,在抽取的50个社区中,这一天共有8个“超标”社区,市政府决定从这8个“超标”社区中任选5个跟踪调查其垃圾来源.设这一天垃圾量不小于30.5吨的社区个数为,求的分布列和数学期望附:若服从正态分布,则,,.
2.(2021·全国·高二课时练习)某学校工会积极组织该校教职工参与“日行万步”活动.界定日行步数不足4千步的人为“不健康生活方式者”,不少于10千步的人为“超健康生活方式者”,其他为“一般生活方式者”.某日,学校工会随机抽取了该校400名教职工,统计他们的日行步数,按步数分组,得到频率分布直方图如图所示.
(1)求400名教职工日行步数(千步)的样本平均数(结果四舍五入保留整数).
(2)由频率分布直方图可以认为该校教职工的日行步数(千步)服从正态分布,其中为样本平均数,标准差的近似值为2.5,求该校被抽取的400名教职工中日行步数(千步)的人数(结果四舍五入保留整数).
(3)用样本估计总体,将频率视为概率.若工会从该校教职工中随机抽取2人作为“日行万步”活动的慰问奖励对象,规定:“不健康生活方式者”给予精神鼓励,奖励金额每人0元;“一般生活方式者”奖励金额每人100元;“超健康生活方式者”奖励金额每人200元.求工会慰问奖励金额X的分布列和数学期望.
附:若随机变量服从正态分布,则,.
3.(2021·全国·高二单元测试)“公平正义”是社会主义和谐社会的重要特征,是社会主义法治的价值追求.考试作为一种公平公正选拔人才的有效途径,正被广泛采用.某单位准备通过考试(按照高分优先录取的原则)录用298名职员,其中275个高薪职位和23个普薪职位.实际报名人数为2000名,考试满分为400分.本次招聘考试的成绩服从正态分布.考试后考生成绩的部分统计结果如下:考试平均成绩是180分,360分及其以上的高分考生有30名.
(1)求最低录取分数(结果保留整数);
(2)考生甲的成绩为286分,若甲被录取,能否获得高薪职位?请说明理由.
参考资料:①当时,令,则.②当时, ,,,.
4.(2021·山东胶州·高二期中)年辽宁、广东、河北、湖北、湖南、江苏、福建、重庆等八省市将全部采用“”的新高考模式.“”指的是语文、数学、外语,这三门科目考试参加统一高考,由教育部考试中心统一命题,以原始成绩计入考生总成绩;“”指的是物理和历史中的一科,考生必须从物理和历史两个科目中选择一科,由各省自主命题,以原始成绩计入考生总成绩.为了让考生更好的适应新高考模式,某省几个地市进行了统一的高考适应性考试.在所有入考考生中有人选考物理,考后物理成绩(满分分)服从正态分布.
(1)分别估计成绩在和分以上者的人数;(运算过程中精确到,最后结果保留为整数)
附1:,,.
(2)本次考试物理成绩服从正态分布.令,则,若本次考试物理成绩的前划定为优秀等级,试估计物理优秀等级划线分大约为多少分?
附2:若,则.
5.(2021·福建泉州·高二期末)2021年3月24日,某些国际服装企业因抵制新疆棉花声明在中国互联网上引发热议.对此,中国外交部发言人25日表示,中国光明磊落,中国人民友善开放,但中国民意不可欺、不可违.某记者随机采访了100名群众,调查群众对此事件的看法,根据统计,抽取的100名群众的年龄频率分布直方图如图所示.
(1)求这100名受访群众年龄的平均数(同一组数据用该区间的中点值代替).
(2)由频率分布直方图可以认为,受访群众的年龄服从正态分布,其中近似为.
①求;
②从年龄在,的受访群众中,按分层抽样的方法,抽出7人参加访谈节目录制,再从这7人中随机抽出3人作为代表发言,设这3位发言人的年龄落在内的人数为,求变量的分布列和数学期望.
参考数据:取,若,则,
联系QQ309000116加入百度网盘群2500G一线老师必备资料一键转存,自动更新,一劳永逸
第10讲 正态分布
【知识梳理】
知识点一 正态曲线与正态分布
1.我们称f(x)=,x∈R,其中μ∈R,σ>0为参数,为正态密度函数,称其图象为正态分布密度曲线,简称正态曲线.
2.若随机变量X的概率密度函数为f(x),则称随机变量X服从正态分布,记为X~N(μ,σ2).
特别地,当μ=0,σ=1时,称随机变量X服从标准正态分布.
3.若X~N(μ,σ2),如图所示,X取值不超过x的概率P(X≤x)为图中区域A的面积,而P(a≤X≤b)为区域B的面积.
知识点二 正态曲线的特点
1.对 x∈R,f(x)>0,它的图象在x轴的上方.
2.曲线与x轴之间的面积为1.
3.曲线是单峰的,它关于直线x=μ对称.
4.曲线在x=μ处达到峰值.
5.当|x|无限增大时,曲线无限接近x轴.
6.当σ一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移,如图①.
7.当μ一定时,曲线的形状由σ确定,σ较小时曲线“瘦高”,表示随机变量X的分布比较集中;σ较大时,曲线“矮胖”,表示随机变量X的分布比较分散,如图②.
知识点三 正态总体在三个特殊区间内取值的概率值及3σ原则
P(μ-σ≤X≤μ+σ)≈0.682 7;
P(μ-2σ≤X≤μ+2σ)≈0.954 5;
P(μ-3σ≤X≤μ+3σ)≈0.997 3.
尽管正态变量的取值范围是(-∞,+∞),但在一次试验中,X的取值几乎总是落在区间[μ-3σ,μ+3σ]内,而在此区间以外取值的概率大约只有0.002 7,通常认为这种情况在一次试验中几乎不可能发生.
在实际应用中,通常认为服从于正态分布N(μ,σ2)的随机变量X只取[μ-3σ,μ+3σ]中的值,这在统计学中称为3σ原则.
【题型归纳】
考点一 正态分布曲线
【例1】(2021·黑龙江·哈尔滨三中高二月考)下列是关于正态曲线性质的说法:
①曲线关于直线对称,且恒位于轴上方;
②曲线关于直线对称,且仅当时才位于轴上方;
③曲线对应的正态密度函数是一个偶函数,因此曲线关于轴对称;
④曲线在处位于最高点,由这一点向左、右两边延伸时,曲线逐渐降低;
⑤曲线的位置由确定,曲线的形状由确定.
其中说法正确的是( )
A.①④⑤ B.②④⑤ C.③④⑤ D.①⑤
【考点精练】
1.(2021·全国·高二课时练习)(多选)甲、乙两类水果的质量(单位:kg)分别服从正态分布,,,其正态分布的密度曲线,,如图所示,则下列说法正确的是( )
A.甲类水果的平均质量
B.乙类水果的质量比甲类水果的质量更集中于均值左右
C.甲类水果的平均质量比乙类水果的平均质量小
D.乙类水果的质量服从的正态分布的参数
2.(2021·全国·高二课时练习)(多选)设X~N(μ1,),Y~N(μ2,),这两个正态分布密度曲线如图所示.下列结论中错误的是( )
A.P(Y≥μ2)≥P(Y≥μ1)
B.P(X≤σ2)≤P(X≤σ1)
C.对任意正数t,P(X≤t)>P(Y≤t)
D.对任意正数t,P(X>t)>P(Y>t)
3.(2021·全国·高二课时练习)(多选)下面给出的关于正态曲线的4个叙述中,正确的有( )
A.曲线在x轴上方,且与x轴不相交
B.当x>μ时,曲线下降,当x<μ时,曲线上升
C.当μ一定时,σ越小,总体分布越分散,σ越大,总体分布越集中
D.曲线关于直线x=μ对称,且当x=μ时,位于最高点
4.(2021·全国·高二课时练习)(多选)一次教学质量检测中,甲、乙、丙三科考试成绩的正态分布密度曲线如图所示,下列说法中不正确的是( )
A.甲科总体的标准差最小
B.丙科总体的平均数最小
C.乙科总体的标准差及平均数都比甲小,比丙大
D.甲、乙、丙总体的平均数不相同
考点二 正态分布(小题)
【例2-1】(2021·全国·高二课时练习)若随机变量,且,则等于( )
A.0.6 B.0.5
C.0.4 D.0.3
【例2-2】(2021·全国·高二课时练习)设随机变量的正态分布密度函数为,,则参数,的值分别是( )
A., B.,
C., D.,
【考点精练】
1.(2021·广东·广州市协和中学高二期中)若随机变量,且,则( )
A.0.6 B.0.5
C.0.4 D.0.3
2.(2021·全国·高二单元测试)某军工企业为某种型号的新式步枪生产了一批枪管,其口径误差(单位:微米)服从正态分布,从已经生产出的枪管中随机取出一只,则其口径误差在区间内的概率为( )
(注:若随机变量服从正态分布,则,)
A.31.7% B.27.18%
C.13. 55% D.4.5%
3.(2021·全国·高二课时练习)在某市2020年3月份的高三线上质量检测考试中,学生的数学成绩服从正态分布N(98,100).已知参加本次考试的全市学生有9 455人,如果某学生在这次考试中的数学成绩是108分,那么他的数学成绩大约排在全市第( )
A.1 500名 B.1 700名
C.4 500名 D.8 000名
4.(2021·全国·高二课时练习)随机变量服从正态分布N(1,4),若,则 ( )
A. B.
C. D.
考点三 正态分布的应用(解答题)
【例3】(2021·黑龙江·哈尔滨市第六中学校高二期中)哈尔滨市香坊区为了了解全区1万名学生的汉字书写水平,在全区范围内进行了汉字听写考试,发现其成绩服从正态分布,现从某校随机抽取了50名学生,将所得成绩整理后,绘制如图所示的频率分布直方图.
(1)估算该校50名学生成绩的平均数(同一组中的数据用该组区间的中点值作代表)
(2)求这50名学生成绩在的人数;
(3)现从该校50名考生成绩在的学生中随机抽取两人,该两人成绩排名(从高到低)在全区前228名的人数记为,求的分布列和数学期望.
参考数据:,则,,
【考点精练】
1(2021·全国·高二课时练习)某市在实施垃圾分类的过程中,从本市人口数量在两万人左右的A类社区(全市共320个)中随机抽取了50个进行调查,统计这50个社区某天产生的垃圾量(单位:吨),得到如下频数分布表,并将这一天垃圾数量超过8吨的社区定为“超标”社区.
垃圾量
频数 5 6 9 12 8 6 7
(1)估计该市类社区这一天垃圾量的平均值.
(2)若该市类社区这一天的垃圾量大致服从正态分布,其中近似为个样本社区的平均值(精确到0.1吨,估计该市类社区中“超标”社区的个数.
(3)根据原始样本数据,在抽取的50个社区中,这一天共有8个“超标”社区,市政府决定从这8个“超标”社区中任选5个跟踪调查其垃圾来源.设这一天垃圾量不小于30.5吨的社区个数为,求的分布列和数学期望附:若服从正态分布,则,,.
2.(2021·全国·高二课时练习)某学校工会积极组织该校教职工参与“日行万步”活动.界定日行步数不足4千步的人为“不健康生活方式者”,不少于10千步的人为“超健康生活方式者”,其他为“一般生活方式者”.某日,学校工会随机抽取了该校400名教职工,统计他们的日行步数,按步数分组,得到频率分布直方图如图所示.
(1)求400名教职工日行步数(千步)的样本平均数(结果四舍五入保留整数).
(2)由频率分布直方图可以认为该校教职工的日行步数(千步)服从正态分布,其中为样本平均数,标准差的近似值为2.5,求该校被抽取的400名教职工中日行步数(千步)的人数(结果四舍五入保留整数).
(3)用样本估计总体,将频率视为概率.若工会从该校教职工中随机抽取2人作为“日行万步”活动的慰问奖励对象,规定:“不健康生活方式者”给予精神鼓励,奖励金额每人0元;“一般生活方式者”奖励金额每人100元;“超健康生活方式者”奖励金额每人200元.求工会慰问奖励金额X的分布列和数学期望.
附:若随机变量服从正态分布,则,.
3.(2021·全国·高二单元测试)“公平正义”是社会主义和谐社会的重要特征,是社会主义法治的价值追求.考试作为一种公平公正选拔人才的有效途径,正被广泛采用.某单位准备通过考试(按照高分优先录取的原则)录用298名职员,其中275个高薪职位和23个普薪职位.实际报名人数为2000名,考试满分为400分.本次招聘考试的成绩服从正态分布.考试后考生成绩的部分统计结果如下:考试平均成绩是180分,360分及其以上的高分考生有30名.
(1)求最低录取分数(结果保留整数);
(2)考生甲的成绩为286分,若甲被录取,能否获得高薪职位?请说明理由.
参考资料:①当时,令,则.②当时, ,,,.
4.(2021·山东胶州·高二期中)年辽宁、广东、河北、湖北、湖南、江苏、福建、重庆等八省市将全部采用“”的新高考模式.“”指的是语文、数学、外语,这三门科目考试参加统一高考,由教育部考试中心统一命题,以原始成绩计入考生总成绩;“”指的是物理和历史中的一科,考生必须从物理和历史两个科目中选择一科,由各省自主命题,以原始成绩计入考生总成绩.为了让考生更好的适应新高考模式,某省几个地市进行了统一的高考适应性考试.在所有入考考生中有人选考物理,考后物理成绩(满分分)服从正态分布.
(1)分别估计成绩在和分以上者的人数;(运算过程中精确到,最后结果保留为整数)
附1:,,.
(2)本次考试物理成绩服从正态分布.令,则,若本次考试物理成绩的前划定为优秀等级,试估计物理优秀等级划线分大约为多少分?
附2:若,则.
5.(2021·福建泉州·高二期末)2021年3月24日,某些国际服装企业因抵制新疆棉花声明在中国互联网上引发热议.对此,中国外交部发言人25日表示,中国光明磊落,中国人民友善开放,但中国民意不可欺、不可违.某记者随机采访了100名群众,调查群众对此事件的看法,根据统计,抽取的100名群众的年龄频率分布直方图如图所示.
(1)求这100名受访群众年龄的平均数(同一组数据用该区间的中点值代替).
(2)由频率分布直方图可以认为,受访群众的年龄服从正态分布,其中近似为.
①求;
②从年龄在,的受访群众中,按分层抽样的方法,抽出7人参加访谈节目录制,再从这7人中随机抽出3人作为代表发言,设这3位发言人的年龄落在内的人数为,求变量的分布列和数学期望.
参考数据:取,若,则,
联系QQ309000116加入百度网盘群2500G一线老师必备资料一键转存,自动更新,一劳永逸
