沪教版数学八年级第二学期20.2一次函数的图像与性质练习试题
文档属性
| 名称 | 沪教版数学八年级第二学期20.2一次函数的图像与性质练习试题 |
|
|
| 格式 | docx | ||
| 文件大小 | 76.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 00:00:00 | ||
图片预览

文档简介
20.2一次函数的图像与性质
(限时60分钟 满分120分)
一、选择(本题共计7小题,每题5分,共计35分)
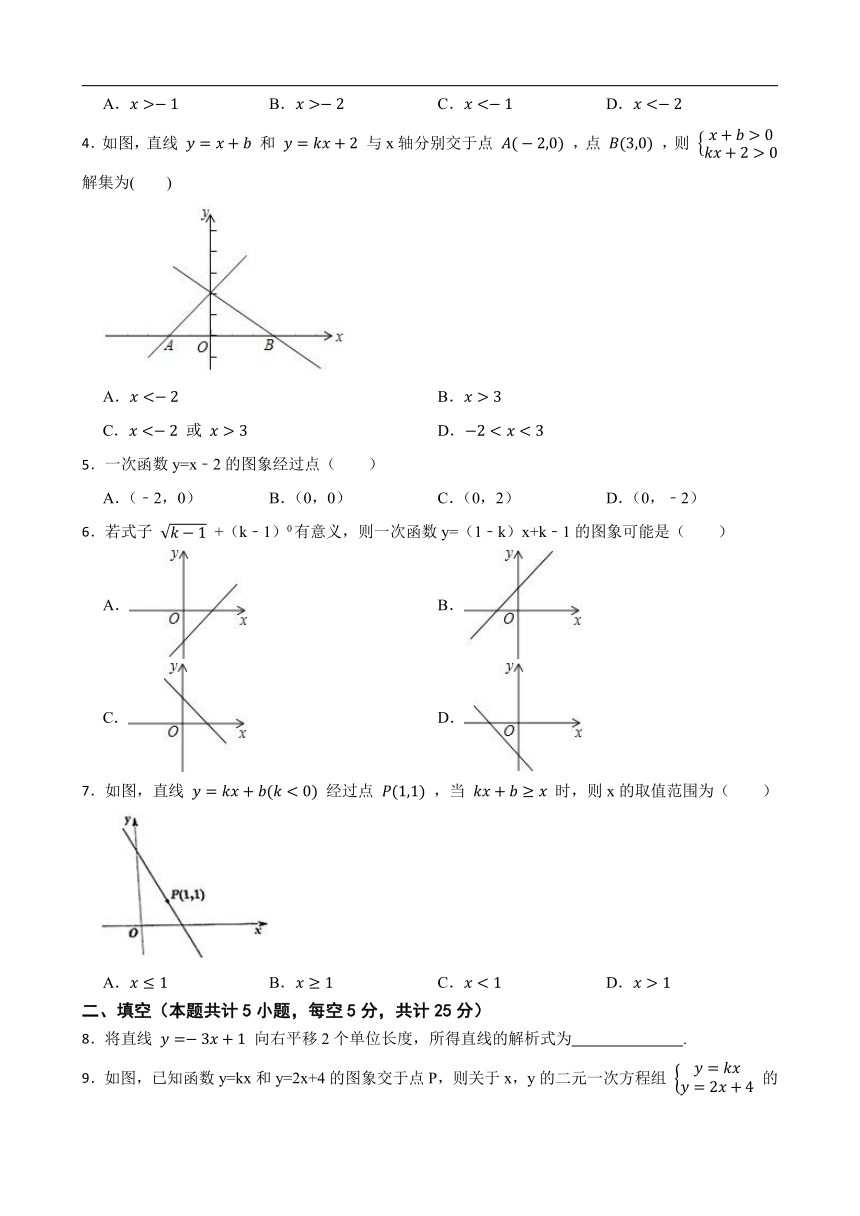
1.一次函数y=kx+b的图象如图所示,则关于x的方程kx+b=﹣1的解为( )
A.x=0 B.x=1 C.x= D.x=﹣2
2.若kb>0,则函数y=kx+b的图象可能是( )
A. B.
C. D.
3.如图,直线 与x轴交于点 ,与y轴交于点 ,则关于x的不等式 的解集为( )
A. B. C. D.
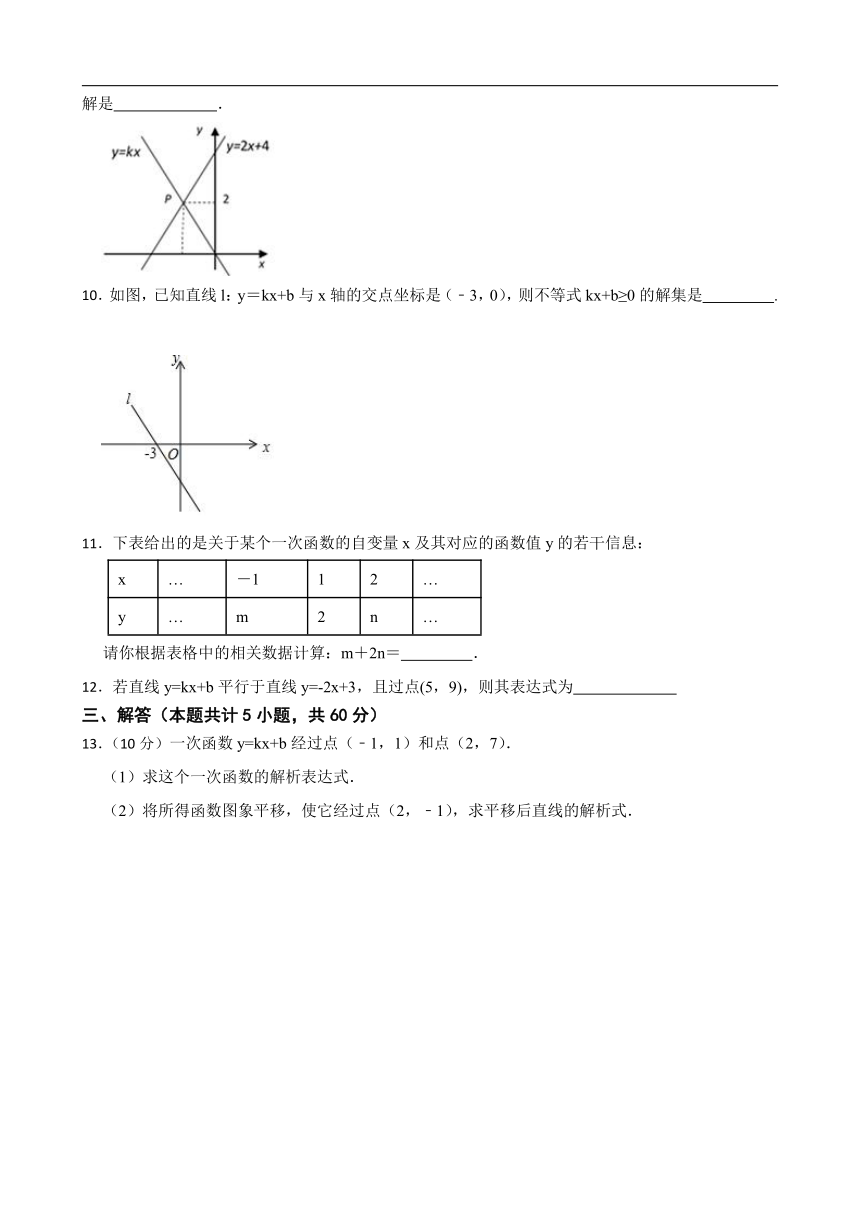
4.如图,直线 和 与x轴分别交于点 ,点 ,则 解集为( )
A. B.
C. 或 D.
5.一次函数y=x﹣2的图象经过点( )
A.(﹣2,0) B.(0,0) C.(0,2) D.(0,﹣2)
6.若式子 +(k﹣1)0有意义,则一次函数y=(1﹣k)x+k﹣1的图象可能是( )
A. B.
C. D.
7.如图,直线 经过点 ,当 时,则x的取值范围为( )
A. B. C. D.
二、填空(本题共计5小题,每空5分,共计25分)
8.将直线 向右平移2个单位长度,所得直线的解析式为 .
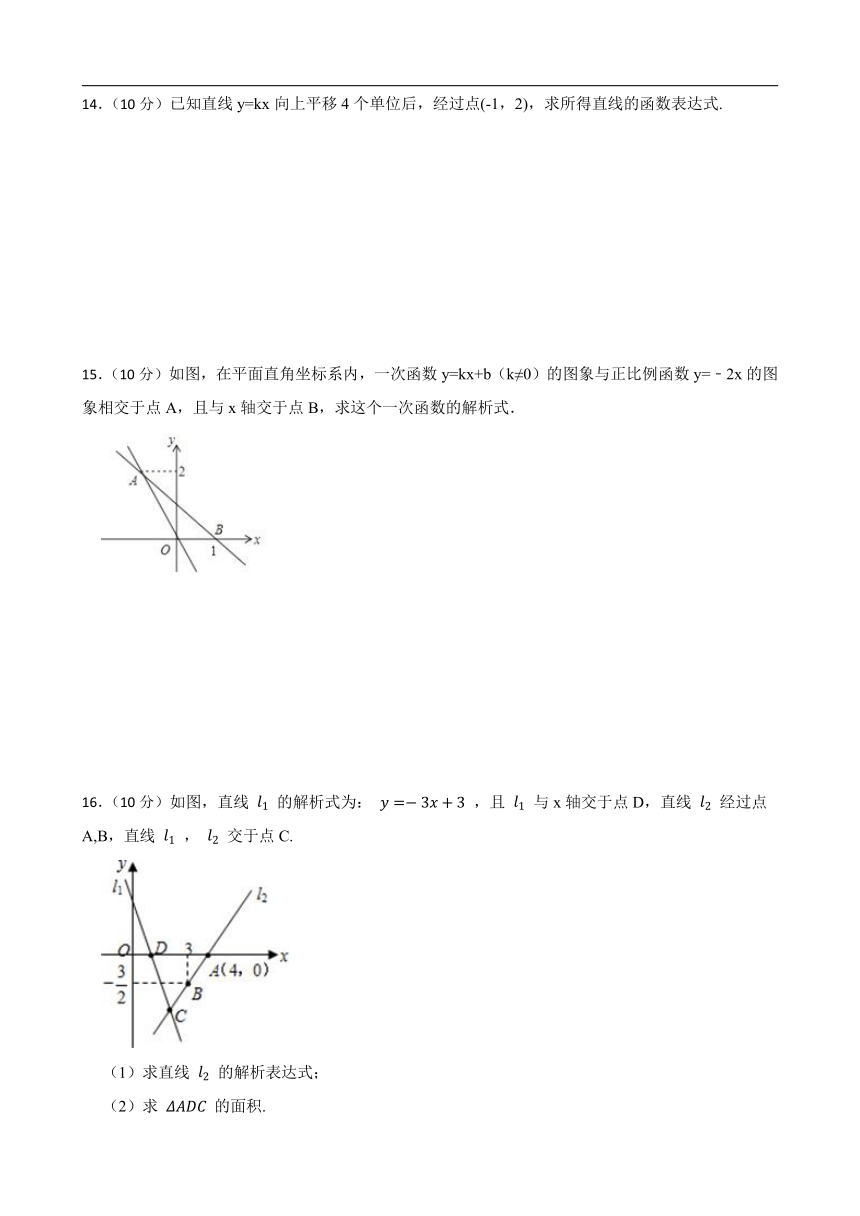
9.如图,已知函数y=kx和y=2x+4的图象交于点P,则关于x,y的二元一次方程组 的解是 .
10.如图,已知直线l:y=kx+b与x轴的交点坐标是(﹣3,0),则不等式kx+b≥0的解集是 .
11.下表给出的是关于某个一次函数的自变量x及其对应的函数值y的若干信息:
x … -1 1 2 …
y … m 2 n …
请你根据表格中的相关数据计算:m+2n= .
12.若直线y=kx+b平行于直线y=-2x+3,且过点(5,9),则其表达式为
三、解答(本题共计5小题,共60分)
13.(10分)一次函数y=kx+b经过点(﹣1,1)和点(2,7).
(1)求这个一次函数的解析表达式.
(2)将所得函数图象平移,使它经过点(2,﹣1),求平移后直线的解析式.
14.(10分)已知直线y=kx向上平移4个单位后,经过点(-1,2),求所得直线的函数表达式.
15.(10分)如图,在平面直角坐标系内,一次函数y=kx+b(k≠0)的图象与正比例函数y=﹣2x的图象相交于点A,且与x轴交于点B,求这个一次函数的解析式.
16.(10分)如图,直线 的解析式为: ,且 与x轴交于点D,直线 经过点A,B,直线 , 交于点C.
(1)求直线 的解析表达式;
(2)求 的面积.
17.(10分)如图,一次函数y=kx+b与反比例函数y= (x>0)的图象交于点A(a,3)和B(3,1).
(1)求一次函数的解析式.
(2)观察图象,写出反比例函数值小于一次函数值时x的取值范围.
(3)点P是线段AB上一点,过点P作PD⊥x轴于点D,交反比例函数图象于点Q,连接OP、OQ,若△POQ的面积为 ,求P点的坐标。
18.(10分)将直线y=﹣x+2先向右平移一个单位长度,再向上平移一个单位长度,所得新的直线l与x轴、y轴分别交于A、B两点,另有一条直线y=x+1.
(1)求l的解析式;
(2)求点A和点B的坐标;
(3)求直线y=x+1与直线l以及y轴所围成的三角形的面积.
答案部分
1.C
2.A
3.A
4.D
5.D
6.C
7.A
8.y= 3x+7
9.
10.x≤﹣3
11.6
12.y=-2x+19
13.解:(1)将点(﹣1,1)和点(2,7)代入解析式得:
,
解得:,
∴一次函数的解析表达式为:y=2x+3;
(2)因为平移,所以直线平行,所以设y=2x+b,
把点(2,﹣1)代入,得b=﹣5,
∴平移后直线的解析式为:y=2x﹣5.
14.解:直线y=kx向上平移4个单位后所得直线的函数表达式为y= kx+4.
把(-1,2)代入y=kx+4,得2=- -k+4,
解得k=2,
所以所得直线的函数表达式为y=2x+4.
15.解:在函数y=﹣2x中令y=2得:﹣2x=2,
解得:x=﹣1,
∴点A坐标为(﹣1,2),
将点A(﹣1,2)、点B(1,0)代入y=kx+b,得:
,
解得:,
∴一次函数解析式为:y=﹣x+1.
16.(1)设直线 的解析式为 .
把 , ; , ,代入 得 ,
∴ ,
∴直线 的解析式为 ;
(2)由 ,
解得
∴ ,
∵ ,
∴
17.(1)解:把 代入 中,得 ,∴
把 代入 中,得 ,∴
把 、 代入 中,得:
解得
∴
(2)解:由图象得:
(3)解:设 且 ,则
∴
∴
解得
∴
18.解:(1)直线y=﹣x+2先向右平移一个单位长度,再向上平移一个单位长度得
y=﹣(x﹣1)+2+1,化简得
y=﹣x+.
(2)当y=0时,0=﹣x+.解得x=7,即A(7,0);
当x=0时,y=,B(0,);
(3)将y=﹣x+和y=x+1联成方程组解得两直线交点为(,).
再求出两直线与y轴交点分别为(0,)和(0,1),
所以三角形面积为××(﹣1)=.
(限时60分钟 满分120分)
一、选择(本题共计7小题,每题5分,共计35分)
1.一次函数y=kx+b的图象如图所示,则关于x的方程kx+b=﹣1的解为( )
A.x=0 B.x=1 C.x= D.x=﹣2
2.若kb>0,则函数y=kx+b的图象可能是( )
A. B.
C. D.
3.如图,直线 与x轴交于点 ,与y轴交于点 ,则关于x的不等式 的解集为( )
A. B. C. D.
4.如图,直线 和 与x轴分别交于点 ,点 ,则 解集为( )
A. B.
C. 或 D.
5.一次函数y=x﹣2的图象经过点( )
A.(﹣2,0) B.(0,0) C.(0,2) D.(0,﹣2)
6.若式子 +(k﹣1)0有意义,则一次函数y=(1﹣k)x+k﹣1的图象可能是( )
A. B.
C. D.
7.如图,直线 经过点 ,当 时,则x的取值范围为( )
A. B. C. D.
二、填空(本题共计5小题,每空5分,共计25分)
8.将直线 向右平移2个单位长度,所得直线的解析式为 .
9.如图,已知函数y=kx和y=2x+4的图象交于点P,则关于x,y的二元一次方程组 的解是 .
10.如图,已知直线l:y=kx+b与x轴的交点坐标是(﹣3,0),则不等式kx+b≥0的解集是 .
11.下表给出的是关于某个一次函数的自变量x及其对应的函数值y的若干信息:
x … -1 1 2 …
y … m 2 n …
请你根据表格中的相关数据计算:m+2n= .
12.若直线y=kx+b平行于直线y=-2x+3,且过点(5,9),则其表达式为
三、解答(本题共计5小题,共60分)
13.(10分)一次函数y=kx+b经过点(﹣1,1)和点(2,7).
(1)求这个一次函数的解析表达式.
(2)将所得函数图象平移,使它经过点(2,﹣1),求平移后直线的解析式.
14.(10分)已知直线y=kx向上平移4个单位后,经过点(-1,2),求所得直线的函数表达式.
15.(10分)如图,在平面直角坐标系内,一次函数y=kx+b(k≠0)的图象与正比例函数y=﹣2x的图象相交于点A,且与x轴交于点B,求这个一次函数的解析式.
16.(10分)如图,直线 的解析式为: ,且 与x轴交于点D,直线 经过点A,B,直线 , 交于点C.
(1)求直线 的解析表达式;
(2)求 的面积.
17.(10分)如图,一次函数y=kx+b与反比例函数y= (x>0)的图象交于点A(a,3)和B(3,1).
(1)求一次函数的解析式.
(2)观察图象,写出反比例函数值小于一次函数值时x的取值范围.
(3)点P是线段AB上一点,过点P作PD⊥x轴于点D,交反比例函数图象于点Q,连接OP、OQ,若△POQ的面积为 ,求P点的坐标。
18.(10分)将直线y=﹣x+2先向右平移一个单位长度,再向上平移一个单位长度,所得新的直线l与x轴、y轴分别交于A、B两点,另有一条直线y=x+1.
(1)求l的解析式;
(2)求点A和点B的坐标;
(3)求直线y=x+1与直线l以及y轴所围成的三角形的面积.
答案部分
1.C
2.A
3.A
4.D
5.D
6.C
7.A
8.y= 3x+7
9.
10.x≤﹣3
11.6
12.y=-2x+19
13.解:(1)将点(﹣1,1)和点(2,7)代入解析式得:
,
解得:,
∴一次函数的解析表达式为:y=2x+3;
(2)因为平移,所以直线平行,所以设y=2x+b,
把点(2,﹣1)代入,得b=﹣5,
∴平移后直线的解析式为:y=2x﹣5.
14.解:直线y=kx向上平移4个单位后所得直线的函数表达式为y= kx+4.
把(-1,2)代入y=kx+4,得2=- -k+4,
解得k=2,
所以所得直线的函数表达式为y=2x+4.
15.解:在函数y=﹣2x中令y=2得:﹣2x=2,
解得:x=﹣1,
∴点A坐标为(﹣1,2),
将点A(﹣1,2)、点B(1,0)代入y=kx+b,得:
,
解得:,
∴一次函数解析式为:y=﹣x+1.
16.(1)设直线 的解析式为 .
把 , ; , ,代入 得 ,
∴ ,
∴直线 的解析式为 ;
(2)由 ,
解得
∴ ,
∵ ,
∴
17.(1)解:把 代入 中,得 ,∴
把 代入 中,得 ,∴
把 、 代入 中,得:
解得
∴
(2)解:由图象得:
(3)解:设 且 ,则
∴
∴
解得
∴
18.解:(1)直线y=﹣x+2先向右平移一个单位长度,再向上平移一个单位长度得
y=﹣(x﹣1)+2+1,化简得
y=﹣x+.
(2)当y=0时,0=﹣x+.解得x=7,即A(7,0);
当x=0时,y=,B(0,);
(3)将y=﹣x+和y=x+1联成方程组解得两直线交点为(,).
再求出两直线与y轴交点分别为(0,)和(0,1),
所以三角形面积为××(﹣1)=.
