第 10 讲 数列综合复习
图片预览


文档简介
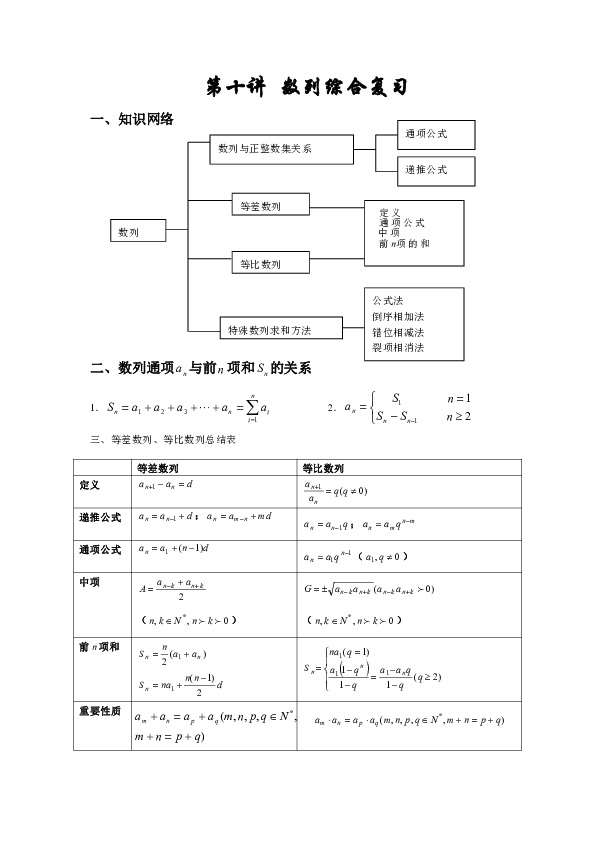
第十讲 数列综合复习
一、知识网络
二、数列通项与前项和的关系
1. 2.
三、等差数列、等比数列总结表
等差数列
等比数列
定义
递推公式
;
;
通项公式
()
中项
()
()
前项和
重要性质
四、裂项法求和
这是分解与组合思想在数列求和中的具体应用. 裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的. 通项分解(裂项)(如常见的几种列项方法):
(1) (2) (3)=
【典型例题】
例1)、等差数列中,( )
A.14 B.15 C.16 D.17
2).等差数列中,,则前 项的和最大。
3).已知等差数列的前10项和为100,前100项和为10,则前110项和为 ?
二、待定系数法(构造法)求通项
求递推式如(p、q为常数)的数列通项,可用待定系数法转化为我们熟知的数列求解,相当如换元法。
例2、已知数列{an}满足a1=1,且an+1 =+2,求.
例3、已知数列{}中且(),,求数列的通项公式。
三、裂项相消法求和
例4:求数列的前n项和.
点拨:①若数列的通项能转化为的形式,常采用裂项相消法求和。
②使用裂项消法求和时,要注意正负项相消时,消去了哪些项,保留了哪些项。
四、错位相减法求和
例5、求和:
五、函数与数列的综合问题
①设是常数,求证:成等比数列;
②若,的前项和是,当时,求
【基础训练A组】一、选择题
1.在数列中,等于 ( )
A. B. C. D.
2.等差数列项的和等于( )
A. B. C. D.
3.等比数列中, 则的前项和为 ( )
A. B. C. D.
4.与,两数的等比中项是 ( )
A. B. C. D.
5.已知一等比数列的前三项依次为,那么是此数列的第 ( )项
A. B. C. D.
6.在公比为整数的等比数列中,如果那么该数列的前项之和为( )
A. B. C. D.
二、填空题
1.等差数列中, 则的公差为______________。
2.数列{}是等差数列,,则_________
3.两个等差数列则 =___________.
4.在等比数列中, 若则a6 =___________.
5.在等比数列中, 若是方程的两根,则 =___________.
6.计算___________.
三、解答题
成等差数列的四个数的和为,第二数与第三数之积为,求这四个数。
在等差数列中, 求的值。
求和:
设等比数列前项和为,若,求数列的公比
5、 设等比数列的前项和为,若求.
【综合训练B组】一、选择题
1.已知等差数列的公差为,若成等比数列, 则 ( )
A. B. C. D.
2.设是等差数列的前n项和,若 ( )
A. B. C. D.
3.若成等差数列,则的值等于 ( )
A. B.或 C. D.
5.在中,是以为第三项, 为第七项的等差数列的公差,
是以为第三项, 为第六项的等比数列的公比,则这个三角形是 ( )
A.钝角三角形 B.锐角三角形 C.等腰直角三角形 D.以上都不对
6.在等差数列中,设,,
,则关系为 ( )
A.等差数列 B.等比数列 C.等差数列或等比数列 D.都不对
7.等比数列的各项均为正数,且,则( )
A. B. C. D.
8、各项均为正数的等比数列的前n项和为Sn,若S10=2,S30=14,则S40等于( )
(A)80 (B)30 (C)26 (D)16
二、填空题
1.等差数列中, 则_________。
2.数列…的一个通项公式是______________________。
3.在正项等比数列中,,则_______。
4.等差数列中,若则=_______。
5.已知数列是等差数列,若,
且,则_________。
6.等比数列前项的和为,则数列前项的和为______________。
7、(2011·广东)等差数列{an}前9项的和等于前4项的和.若a1=1,ak+a4=0,则k=________.
三、解答题
1.求和:
2.已知数列的通项公式,如果,求数列的前项和。
3.在等比数列中,求的范围。
【提高训练C组】一、选择题
1.数列的通项公式,则该数列的前( )项之和等于。
A. B. C. D.
2.在等差数列中,若,则的值为 ( )
A. B. C. D.
4.在等差数列中,,则为( )
A. B. C. D.
5.已知等差数列项和为等于( )
A. B. C. D.
6.等差数列,的前项和分别为,,若,则=( )
A. B. C. D.
二、填空题
1.已知数列中,,,则数列通项___________。
2.已知数列的,则=_____________。
3.三个不同的实数成等差数列,且成等比数列,则_________。
4.在等差数列中,公差,前项的和,
则=_____________。
5.若等差数列中,则
6.一个等比数列各项均为正数,且它的任何一项都等于它的后面两项的和,
则公比为_______________。
三、解答题
已知数列的前项和,求
一个有穷等比数列的首项为,项数为偶数,如果其奇数项的和为,偶数项的和为,求此数列的公比和项数。
一、知识网络
二、数列通项与前项和的关系
1. 2.
三、等差数列、等比数列总结表
等差数列
等比数列
定义
递推公式
;
;
通项公式
()
中项
()
()
前项和
重要性质
四、裂项法求和
这是分解与组合思想在数列求和中的具体应用. 裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的. 通项分解(裂项)(如常见的几种列项方法):
(1) (2) (3)=
【典型例题】
例1)、等差数列中,( )
A.14 B.15 C.16 D.17
2).等差数列中,,则前 项的和最大。
3).已知等差数列的前10项和为100,前100项和为10,则前110项和为 ?
二、待定系数法(构造法)求通项
求递推式如(p、q为常数)的数列通项,可用待定系数法转化为我们熟知的数列求解,相当如换元法。
例2、已知数列{an}满足a1=1,且an+1 =+2,求.
例3、已知数列{}中且(),,求数列的通项公式。
三、裂项相消法求和
例4:求数列的前n项和.
点拨:①若数列的通项能转化为的形式,常采用裂项相消法求和。
②使用裂项消法求和时,要注意正负项相消时,消去了哪些项,保留了哪些项。
四、错位相减法求和
例5、求和:
五、函数与数列的综合问题
①设是常数,求证:成等比数列;
②若,的前项和是,当时,求
【基础训练A组】一、选择题
1.在数列中,等于 ( )
A. B. C. D.
2.等差数列项的和等于( )
A. B. C. D.
3.等比数列中, 则的前项和为 ( )
A. B. C. D.
4.与,两数的等比中项是 ( )
A. B. C. D.
5.已知一等比数列的前三项依次为,那么是此数列的第 ( )项
A. B. C. D.
6.在公比为整数的等比数列中,如果那么该数列的前项之和为( )
A. B. C. D.
二、填空题
1.等差数列中, 则的公差为______________。
2.数列{}是等差数列,,则_________
3.两个等差数列则 =___________.
4.在等比数列中, 若则a6 =___________.
5.在等比数列中, 若是方程的两根,则 =___________.
6.计算___________.
三、解答题
成等差数列的四个数的和为,第二数与第三数之积为,求这四个数。
在等差数列中, 求的值。
求和:
设等比数列前项和为,若,求数列的公比
5、 设等比数列的前项和为,若求.
【综合训练B组】一、选择题
1.已知等差数列的公差为,若成等比数列, 则 ( )
A. B. C. D.
2.设是等差数列的前n项和,若 ( )
A. B. C. D.
3.若成等差数列,则的值等于 ( )
A. B.或 C. D.
5.在中,是以为第三项, 为第七项的等差数列的公差,
是以为第三项, 为第六项的等比数列的公比,则这个三角形是 ( )
A.钝角三角形 B.锐角三角形 C.等腰直角三角形 D.以上都不对
6.在等差数列中,设,,
,则关系为 ( )
A.等差数列 B.等比数列 C.等差数列或等比数列 D.都不对
7.等比数列的各项均为正数,且,则( )
A. B. C. D.
8、各项均为正数的等比数列的前n项和为Sn,若S10=2,S30=14,则S40等于( )
(A)80 (B)30 (C)26 (D)16
二、填空题
1.等差数列中, 则_________。
2.数列…的一个通项公式是______________________。
3.在正项等比数列中,,则_______。
4.等差数列中,若则=_______。
5.已知数列是等差数列,若,
且,则_________。
6.等比数列前项的和为,则数列前项的和为______________。
7、(2011·广东)等差数列{an}前9项的和等于前4项的和.若a1=1,ak+a4=0,则k=________.
三、解答题
1.求和:
2.已知数列的通项公式,如果,求数列的前项和。
3.在等比数列中,求的范围。
【提高训练C组】一、选择题
1.数列的通项公式,则该数列的前( )项之和等于。
A. B. C. D.
2.在等差数列中,若,则的值为 ( )
A. B. C. D.
4.在等差数列中,,则为( )
A. B. C. D.
5.已知等差数列项和为等于( )
A. B. C. D.
6.等差数列,的前项和分别为,,若,则=( )
A. B. C. D.
二、填空题
1.已知数列中,,,则数列通项___________。
2.已知数列的,则=_____________。
3.三个不同的实数成等差数列,且成等比数列,则_________。
4.在等差数列中,公差,前项的和,
则=_____________。
5.若等差数列中,则
6.一个等比数列各项均为正数,且它的任何一项都等于它的后面两项的和,
则公比为_______________。
三、解答题
已知数列的前项和,求
一个有穷等比数列的首项为,项数为偶数,如果其奇数项的和为,偶数项的和为,求此数列的公比和项数。
