沪科版七年级下册10.1相交线(第3课时)课件(共21PPT)
文档属性
| 名称 | 沪科版七年级下册10.1相交线(第3课时)课件(共21PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1019.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 09:41:07 | ||
图片预览




文档简介
(共21张PPT)
10.1 相 交 线
沪科版七年级下册
第10章 相交线、平行线与平移
第三课时 垂线段及其性质
A
D
C
l
m
O
B
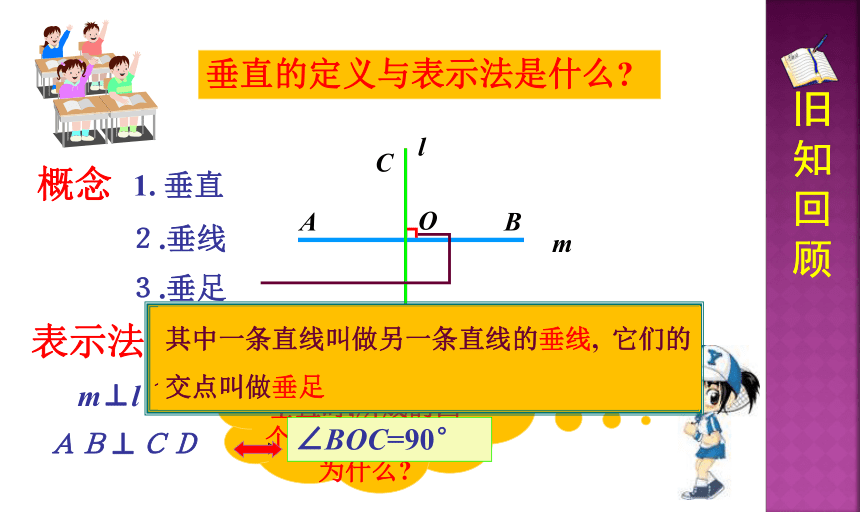
概念
1. 垂直
2.垂线
3.垂足
表示法
AB⊥CD
m⊥l
垂直的定义与表示法是什么
当两条直线互相垂直时,所成的四个角都是直角吗 为什么
∠BOC=90°
在两条直线相交所成的四个角中,如果有一个角是直角,就说这两条直线互相垂直
其中一条直线叫做另一条直线的垂线, 它们的交点叫做垂足
旧知回顾
旧知回顾
垂线的性质(1)
在同一平面内,过一点有且只有一条直线与已知直线垂直。
一、放;二、移;三、画线
垂线的画法
旧知回顾
数学通用课支持不同终端用户快捷上网,手机浏览器自主研发的X5内核在速度、流量节省、稳定性上业内领先
学习目标
1
2
3
掌握点到直线之间的距离,并且能够测量点到直线的距离
通过垂线和垂线段的相关知识学习,进一步发展学生的空间观念,培养不断探索发现新知识的精神
了解垂线段的概念和性质,并且会进行简单的推理
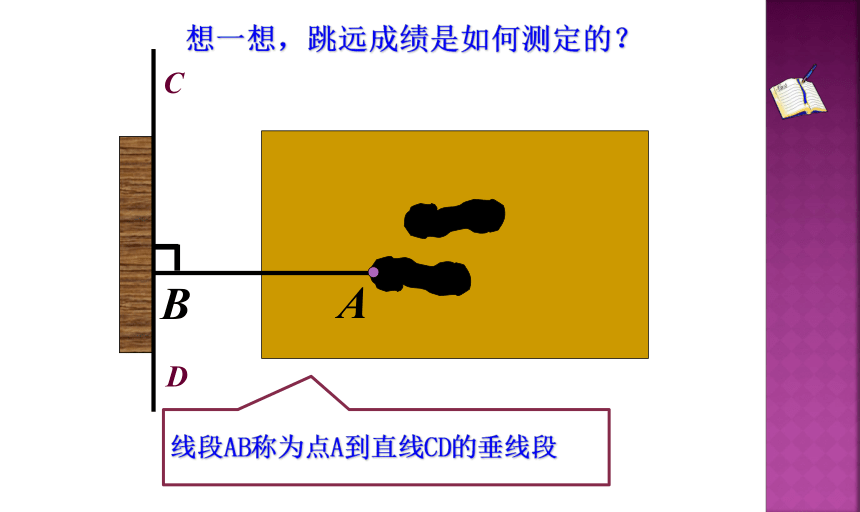
在奥运会的跳远比赛中,裁判员在测量运动员的跳远成绩时,拉紧的皮尺与起跳线有什么关系?这样做的依据是什么?
新知导入
A
B
想一想,跳远成绩是如何测定的?
线段AB称为点A到直线CD的垂线段
C
D
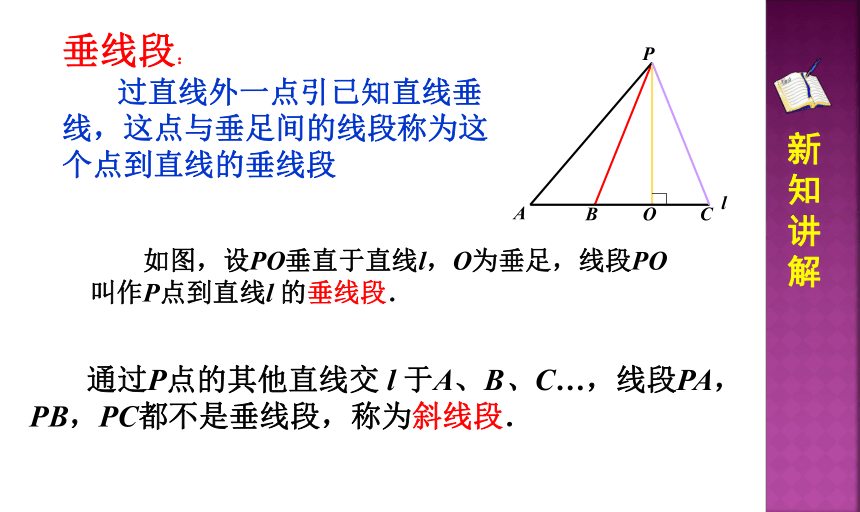
如图,设PO垂直于直线l,O为垂足,线段PO叫作P点到直线l 的垂线段.
P
B
l
O
A
C
通过P点的其他直线交 l 于A、B、C…,线段PA,PB,PC都不是垂线段,称为斜线段.
垂线段:
过直线外一点引已知直线垂线,这点与垂足间的线段称为这个点到直线的垂线段
新知讲解
l
P
O
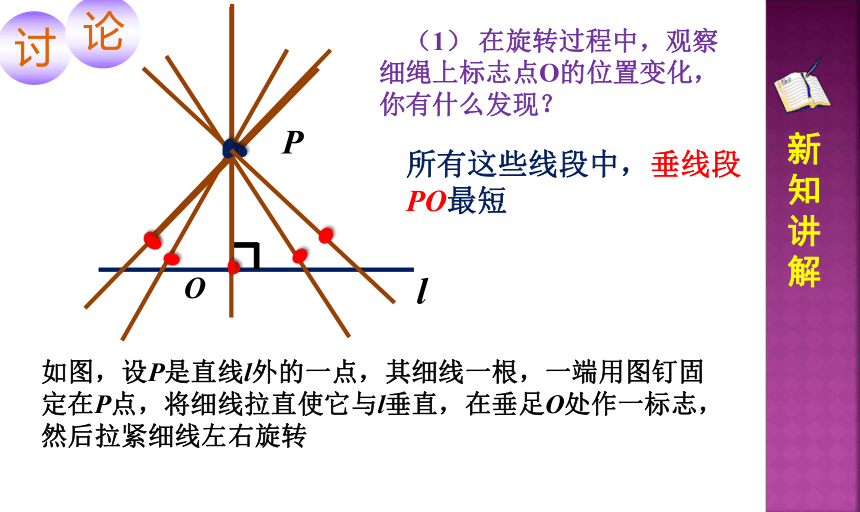
如图,设P是直线l外的一点,其细线一根,一端用图钉固定在P点,将细线拉直使它与l垂直,在垂足O处作一标志,然后拉紧细线左右旋转
所有这些线段中,垂线段PO最短
(1) 在旋转过程中,观察细绳上标志点O的位置变化,你有什么发现?
讨
论
新知讲解
C
A
B
F
E
D
G
H
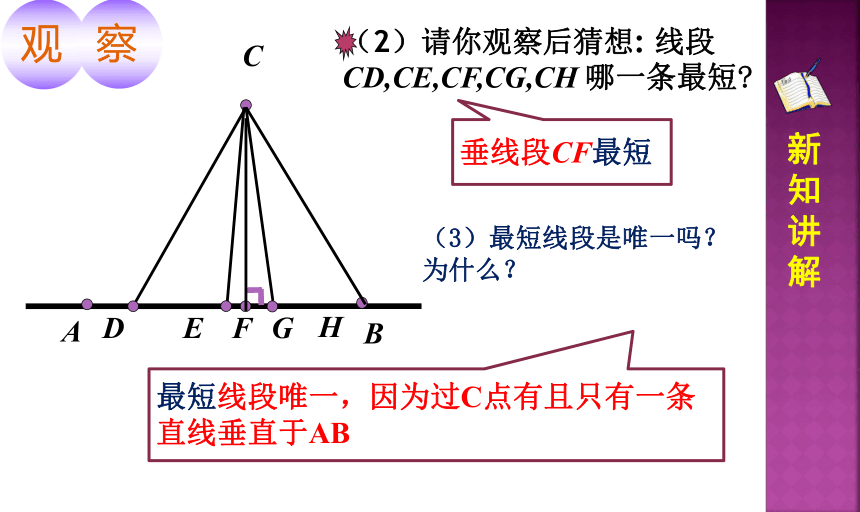
(2)请你观察后猜想: 线段CD,CE,CF,CG,CH 哪一条最短
观
察
(3)最短线段是唯一吗?为什么?
垂线段CF最短
最短线段唯一,因为过C点有且只有一条直线垂直于AB
新知讲解
(3)你能用一句话总结出观察得出的结论吗?
连接直线外一点与直线上各点的所有线段中,垂线段最短。
简单说成:垂线段最短.
垂线性质2:
连接直线外一点与直线上各点的所有线段中 垂线段最短.
A
B
C
D
E
l
新知讲解
由直线外一点向直线引垂线,这点与垂足间的线段叫做垂线段。
l
A
P
直线外一点到这条直线的垂线段的长度,叫做点直线的距离。
点到直线的距离
如图,过点P作l的垂线,垂足为A点。
线段PA的长度叫做点P到直线l的距离。
新知讲解
垂线是一条 线;
垂线段是一条 ,是图形;
点到直线的距离是垂线段的 ,是一个数量,不能说垂线段是距离。
垂线、垂线段与点到直线的距离的区别
直
线段
长度
我发现
三个不同的概念
新知讲解
思考:体育课上应该怎样测量同学们的跳远成绩?为什么?
测量身体的最后着地点到跳板前边缘所在直线的距离
垂线段最短
新知讲解
如图,要把河中的水引到农田P处,在比例尺为1:100 000的图中,求渠道最短距离。
P
直线外一点p到水渠所在直线的垂线段长度
思考:最短距离是哪条线段的长度,为什么?
过点p作河水所在直线的垂线,垂线段PA为水渠所在位置
垂线段最短
A
若量得线段PA=3cm,
则水渠长度=3×100000
=300000(cm)=3(千米)
新知讲解
巩固练习
1、判断
1)一条直线的垂线只能画一条( )
2)两直线相交所构成的四个角相等,则这两直线互相垂直( )
3)点到直线的垂线段就是点到直线的距离( )
4)过一点有且只有一条直线与已知直线垂直( )
×
√
√
×
2.过一条线段外一点,做这条直线的垂线,垂足在( )
A.这条线段上 B.这条线段的端点初、
C.这条线段的延长线上 D.以上都有可能
D
3.点到直线的距离是指( )
A.直线外一点到这条直线的垂线段
B.直线外一点到这条直线的垂线段的长度
C.直线外一点到这条直线的垂线的长度
D.直线外一点到这条线上任意一点的距离
B
巩固练习
4.如图, AC⊥BC, ∠C=90° ,线段AC、BC、CD中最短的是 ( )
A. AC B. BC C. CD D. 不能确定
C
D
┓
┓
A
B
C
5.如图,AD⊥BD,BC⊥CD,AB=a cm,BC=b cm,则BD的取值范围是( )
A.小于a cm B.大于b cm
C.小于a cm或大于b cm D.小于a cm且大于b cm
┓
┓
a
A
D
C
B
b
D
巩固练习
6、已知点A,与点A的距离是5cm的直线可( )
A. 1条 B. 2条 C. 3条 D. 无数条
D
7.如图,OM⊥NP,ON⊥NP,所以ON与OM重合,理由是( )
A.两点确定一条直线 B.同一平面内,经过有且只有一条直线与已知直线垂直 C.过一点只能作一条直线 D.垂线段最短
B
┓
M
N
P
O
巩固练习
┓
8.如图,BC⊥AC,CB=8cm,AC=6cm,AB=10cm,
那么点B到AC的距离是 ,
点A到BC的距离是 ,
点C到AB的距离是 。
A
C
B
8cm
6cm
4.8cm
┓
9、如图OA⊥OC,OB⊥OD,且∠BOC=α,
则∠AOD= .
180°- α
A
B
C
D
O
巩固练习
10.如图,AO⊥FD,OD为∠BOC的平分线,OE为射线OB的反向延长线,若∠AOB=40°,求∠EOF、∠COE的度数.
A
F
D
O
B
C
E
解:∵AO⊥OD且∠AOB=40°,
∴∠BOD=90°-40°=50°,
∴∠EOF=50°.
又∵OD平分∠BOC,
∴∠DOC=∠BOD=50°,
∴∠COE=180°-50°-50°=80°.
巩固练习
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
课堂小结
点到直线的距离.
新知总结
10.1 相 交 线
沪科版七年级下册
第10章 相交线、平行线与平移
第三课时 垂线段及其性质
A
D
C
l
m
O
B
概念
1. 垂直
2.垂线
3.垂足
表示法
AB⊥CD
m⊥l
垂直的定义与表示法是什么
当两条直线互相垂直时,所成的四个角都是直角吗 为什么
∠BOC=90°
在两条直线相交所成的四个角中,如果有一个角是直角,就说这两条直线互相垂直
其中一条直线叫做另一条直线的垂线, 它们的交点叫做垂足
旧知回顾
旧知回顾
垂线的性质(1)
在同一平面内,过一点有且只有一条直线与已知直线垂直。
一、放;二、移;三、画线
垂线的画法
旧知回顾
数学通用课支持不同终端用户快捷上网,手机浏览器自主研发的X5内核在速度、流量节省、稳定性上业内领先
学习目标
1
2
3
掌握点到直线之间的距离,并且能够测量点到直线的距离
通过垂线和垂线段的相关知识学习,进一步发展学生的空间观念,培养不断探索发现新知识的精神
了解垂线段的概念和性质,并且会进行简单的推理
在奥运会的跳远比赛中,裁判员在测量运动员的跳远成绩时,拉紧的皮尺与起跳线有什么关系?这样做的依据是什么?
新知导入
A
B
想一想,跳远成绩是如何测定的?
线段AB称为点A到直线CD的垂线段
C
D
如图,设PO垂直于直线l,O为垂足,线段PO叫作P点到直线l 的垂线段.
P
B
l
O
A
C
通过P点的其他直线交 l 于A、B、C…,线段PA,PB,PC都不是垂线段,称为斜线段.
垂线段:
过直线外一点引已知直线垂线,这点与垂足间的线段称为这个点到直线的垂线段
新知讲解
l
P
O
如图,设P是直线l外的一点,其细线一根,一端用图钉固定在P点,将细线拉直使它与l垂直,在垂足O处作一标志,然后拉紧细线左右旋转
所有这些线段中,垂线段PO最短
(1) 在旋转过程中,观察细绳上标志点O的位置变化,你有什么发现?
讨
论
新知讲解
C
A
B
F
E
D
G
H
(2)请你观察后猜想: 线段CD,CE,CF,CG,CH 哪一条最短
观
察
(3)最短线段是唯一吗?为什么?
垂线段CF最短
最短线段唯一,因为过C点有且只有一条直线垂直于AB
新知讲解
(3)你能用一句话总结出观察得出的结论吗?
连接直线外一点与直线上各点的所有线段中,垂线段最短。
简单说成:垂线段最短.
垂线性质2:
连接直线外一点与直线上各点的所有线段中 垂线段最短.
A
B
C
D
E
l
新知讲解
由直线外一点向直线引垂线,这点与垂足间的线段叫做垂线段。
l
A
P
直线外一点到这条直线的垂线段的长度,叫做点直线的距离。
点到直线的距离
如图,过点P作l的垂线,垂足为A点。
线段PA的长度叫做点P到直线l的距离。
新知讲解
垂线是一条 线;
垂线段是一条 ,是图形;
点到直线的距离是垂线段的 ,是一个数量,不能说垂线段是距离。
垂线、垂线段与点到直线的距离的区别
直
线段
长度
我发现
三个不同的概念
新知讲解
思考:体育课上应该怎样测量同学们的跳远成绩?为什么?
测量身体的最后着地点到跳板前边缘所在直线的距离
垂线段最短
新知讲解
如图,要把河中的水引到农田P处,在比例尺为1:100 000的图中,求渠道最短距离。
P
直线外一点p到水渠所在直线的垂线段长度
思考:最短距离是哪条线段的长度,为什么?
过点p作河水所在直线的垂线,垂线段PA为水渠所在位置
垂线段最短
A
若量得线段PA=3cm,
则水渠长度=3×100000
=300000(cm)=3(千米)
新知讲解
巩固练习
1、判断
1)一条直线的垂线只能画一条( )
2)两直线相交所构成的四个角相等,则这两直线互相垂直( )
3)点到直线的垂线段就是点到直线的距离( )
4)过一点有且只有一条直线与已知直线垂直( )
×
√
√
×
2.过一条线段外一点,做这条直线的垂线,垂足在( )
A.这条线段上 B.这条线段的端点初、
C.这条线段的延长线上 D.以上都有可能
D
3.点到直线的距离是指( )
A.直线外一点到这条直线的垂线段
B.直线外一点到这条直线的垂线段的长度
C.直线外一点到这条直线的垂线的长度
D.直线外一点到这条线上任意一点的距离
B
巩固练习
4.如图, AC⊥BC, ∠C=90° ,线段AC、BC、CD中最短的是 ( )
A. AC B. BC C. CD D. 不能确定
C
D
┓
┓
A
B
C
5.如图,AD⊥BD,BC⊥CD,AB=a cm,BC=b cm,则BD的取值范围是( )
A.小于a cm B.大于b cm
C.小于a cm或大于b cm D.小于a cm且大于b cm
┓
┓
a
A
D
C
B
b
D
巩固练习
6、已知点A,与点A的距离是5cm的直线可( )
A. 1条 B. 2条 C. 3条 D. 无数条
D
7.如图,OM⊥NP,ON⊥NP,所以ON与OM重合,理由是( )
A.两点确定一条直线 B.同一平面内,经过有且只有一条直线与已知直线垂直 C.过一点只能作一条直线 D.垂线段最短
B
┓
M
N
P
O
巩固练习
┓
8.如图,BC⊥AC,CB=8cm,AC=6cm,AB=10cm,
那么点B到AC的距离是 ,
点A到BC的距离是 ,
点C到AB的距离是 。
A
C
B
8cm
6cm
4.8cm
┓
9、如图OA⊥OC,OB⊥OD,且∠BOC=α,
则∠AOD= .
180°- α
A
B
C
D
O
巩固练习
10.如图,AO⊥FD,OD为∠BOC的平分线,OE为射线OB的反向延长线,若∠AOB=40°,求∠EOF、∠COE的度数.
A
F
D
O
B
C
E
解:∵AO⊥OD且∠AOB=40°,
∴∠BOD=90°-40°=50°,
∴∠EOF=50°.
又∵OD平分∠BOC,
∴∠DOC=∠BOD=50°,
∴∠COE=180°-50°-50°=80°.
巩固练习
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
课堂小结
点到直线的距离.
新知总结
