河北省保定市定兴中学2012-2013学年高二3月月考数学(文)试题(无答案)
文档属性
| 名称 | 河北省保定市定兴中学2012-2013学年高二3月月考数学(文)试题(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 113.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-18 16:33:15 | ||
图片预览


文档简介
定兴中学2012-2013学年高二3月月考数学(文)试题
一、选择题(本大题共12小题。每小题5分。共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.抛物线的焦点坐标是( )
A.(2,0) B.(,0) C.(0,) D. (0,2)
2.命题P:x=1,命题:(x-1)(x+2)=0则的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
3.分析法是从要证明的结论出发,逐步寻求使结论成立的( )
A.充分条件 B.必要条件 C.充要条件 D.等价条件
4.在某项体育比赛中,七位裁判为一选手打出分数的茎叶图如图,
去掉一个最高分和一个最低分后,该选手的平均分为( )
A.90 B.91 C.92 D.93
5.对一个命题的证明,下列说法错误的是( )
A.若能用分析法,必能用综合法
B.若用综合法或分析法证明难度较大时,可考虑分析法与综合法的合用等方法
C.若用直接证法难度较大时,可考虑反证法
D.用反证法就是要证结论的反面成立
6.在上随机取一个数,则的概率为( )
A. B. C. D.
7.(1)已知,求证,用反证法证明时,可假设,
(2)已知,求证方程的两根的绝对值都小于1.用反证法证明时可假设方程有一根的绝对值大于或等于1,即假设,以下结论正确的是( )
A.与的假设都错误 B.与的假设都正确
C.的假设正确;的假设错误 D.的假设错误;的假设正确
8.若、为双曲线C:的左、右焦点,点P在曲线C上,,则 ∣∣∣∣( )
A.2 B.4 C.6 D.8
9. 若某程序框图如图所示,则该程序运行后输出的值是( )
A. 11 B. 10 C. 9 D.8
10.已知三个数成等比数列,则圆锥曲线
的离心率为( )
A. B. C.或 D.或
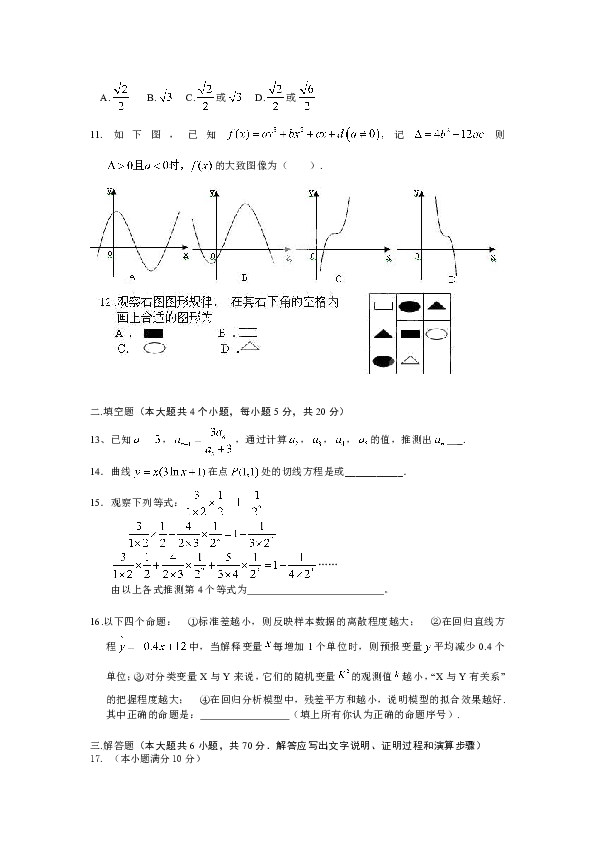
11.如下图,已知记则的大致图像为( ).
二.填空题(本大题共4个小题,每小题5分,共20分)
13、已知,,通过计算,,,的值,推测出___.
14.曲线在点处的切线方程是或___________.
15.观察下列等式:
……
由以上各式推测第4个等式为 。
16.以下四个命题: ①标准差越小,则反映样本数据的离散程度越大; ②在回归直线方程中,当解释变量每增加1个单位时,则预报变量平均减少0.4个单位;③对分类变量X与Y来说,它们的随机变量的观测值越小,“X与Y有关系”的把握程度越大; ④在回归分析模型中,残差平方和越小,说明模型的拟合效果越好.其中正确的命题是: (填上所有你认为正确的命题序号).
三.解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程和演算步骤)
17. (本小题满分10分)
求证:
18.(本小题满分12分)
在中,三个内角A,B,C的对边分别为a,b,c,且A,B,C成等差数列,a,b,c成等比数列.
求证:为等边三角形.
20.(本小题满分12分)已知直线y=-x+m与椭圆相交于A、B两点,若椭圆的离心率为,焦距为2.
(Ⅰ)求椭圆方程;
(Ⅱ)若向量·=0(其中0为坐标原点),求m的值.
21. (本大题满分12分)
一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如下
一、选择题(本大题共12小题。每小题5分。共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.抛物线的焦点坐标是( )
A.(2,0) B.(,0) C.(0,) D. (0,2)
2.命题P:x=1,命题:(x-1)(x+2)=0则的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
3.分析法是从要证明的结论出发,逐步寻求使结论成立的( )
A.充分条件 B.必要条件 C.充要条件 D.等价条件
4.在某项体育比赛中,七位裁判为一选手打出分数的茎叶图如图,
去掉一个最高分和一个最低分后,该选手的平均分为( )
A.90 B.91 C.92 D.93
5.对一个命题的证明,下列说法错误的是( )
A.若能用分析法,必能用综合法
B.若用综合法或分析法证明难度较大时,可考虑分析法与综合法的合用等方法
C.若用直接证法难度较大时,可考虑反证法
D.用反证法就是要证结论的反面成立
6.在上随机取一个数,则的概率为( )
A. B. C. D.
7.(1)已知,求证,用反证法证明时,可假设,
(2)已知,求证方程的两根的绝对值都小于1.用反证法证明时可假设方程有一根的绝对值大于或等于1,即假设,以下结论正确的是( )
A.与的假设都错误 B.与的假设都正确
C.的假设正确;的假设错误 D.的假设错误;的假设正确
8.若、为双曲线C:的左、右焦点,点P在曲线C上,,则 ∣∣∣∣( )
A.2 B.4 C.6 D.8
9. 若某程序框图如图所示,则该程序运行后输出的值是( )
A. 11 B. 10 C. 9 D.8
10.已知三个数成等比数列,则圆锥曲线
的离心率为( )
A. B. C.或 D.或
11.如下图,已知记则的大致图像为( ).
二.填空题(本大题共4个小题,每小题5分,共20分)
13、已知,,通过计算,,,的值,推测出___.
14.曲线在点处的切线方程是或___________.
15.观察下列等式:
……
由以上各式推测第4个等式为 。
16.以下四个命题: ①标准差越小,则反映样本数据的离散程度越大; ②在回归直线方程中,当解释变量每增加1个单位时,则预报变量平均减少0.4个单位;③对分类变量X与Y来说,它们的随机变量的观测值越小,“X与Y有关系”的把握程度越大; ④在回归分析模型中,残差平方和越小,说明模型的拟合效果越好.其中正确的命题是: (填上所有你认为正确的命题序号).
三.解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程和演算步骤)
17. (本小题满分10分)
求证:
18.(本小题满分12分)
在中,三个内角A,B,C的对边分别为a,b,c,且A,B,C成等差数列,a,b,c成等比数列.
求证:为等边三角形.
20.(本小题满分12分)已知直线y=-x+m与椭圆相交于A、B两点,若椭圆的离心率为,焦距为2.
(Ⅰ)求椭圆方程;
(Ⅱ)若向量·=0(其中0为坐标原点),求m的值.
21. (本大题满分12分)
一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如下
同课章节目录
