沪科版数学七年级下册 8.2 多项式与多项式相乘 课件(共22张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 8.2 多项式与多项式相乘 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 11:27:19 | ||
图片预览

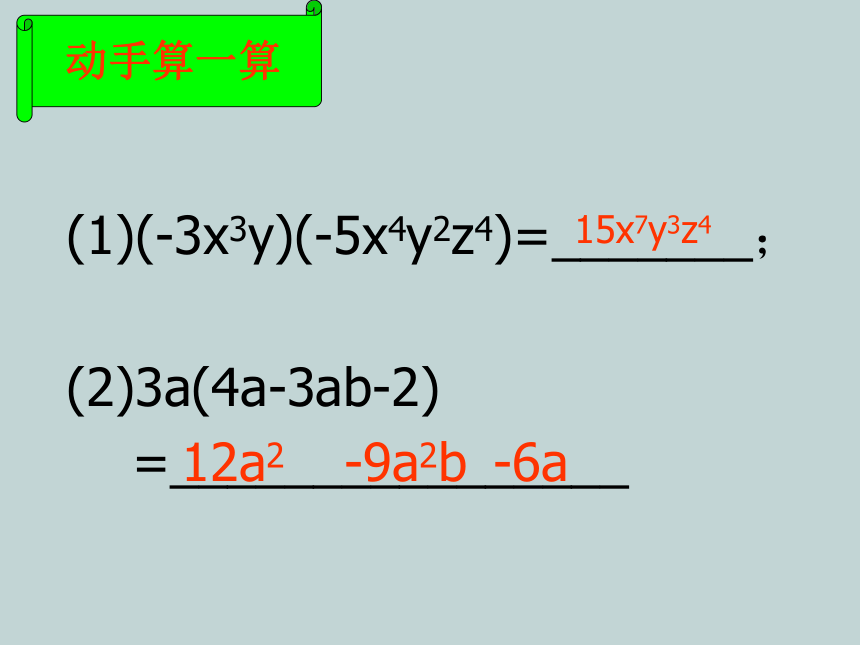



文档简介
(共22张PPT)
8.2.3多项式与多项式相乘
(1)(-3x3y)(-5x4y2z4)=_______;
(2)3a(4a-3ab-2)
=________________
15x7y3z4
12a2
-9a2b
-6a
动手算一算
1、单项式乘以单项式的法则?
思考并回答
2、单项式乘以多项式的法则?
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加。
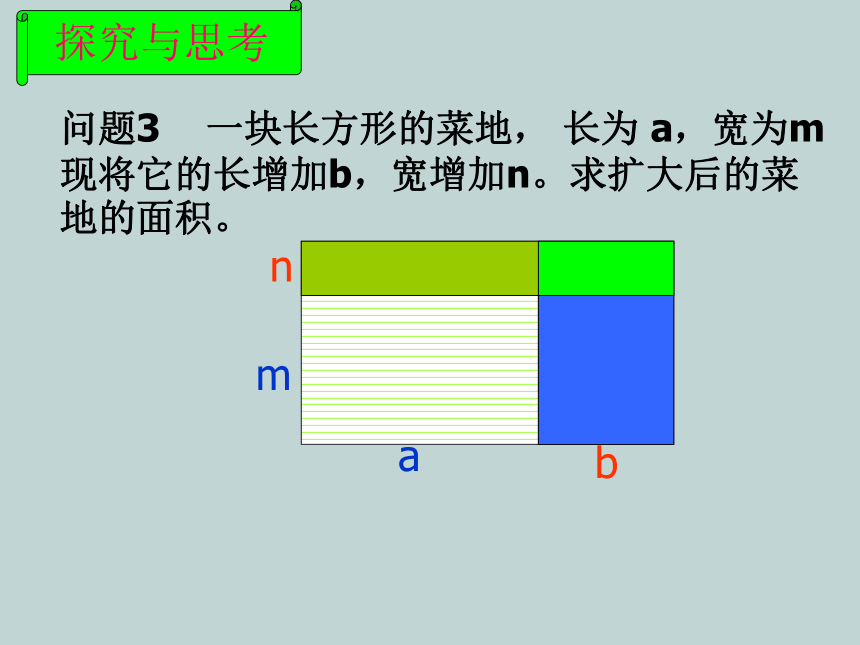
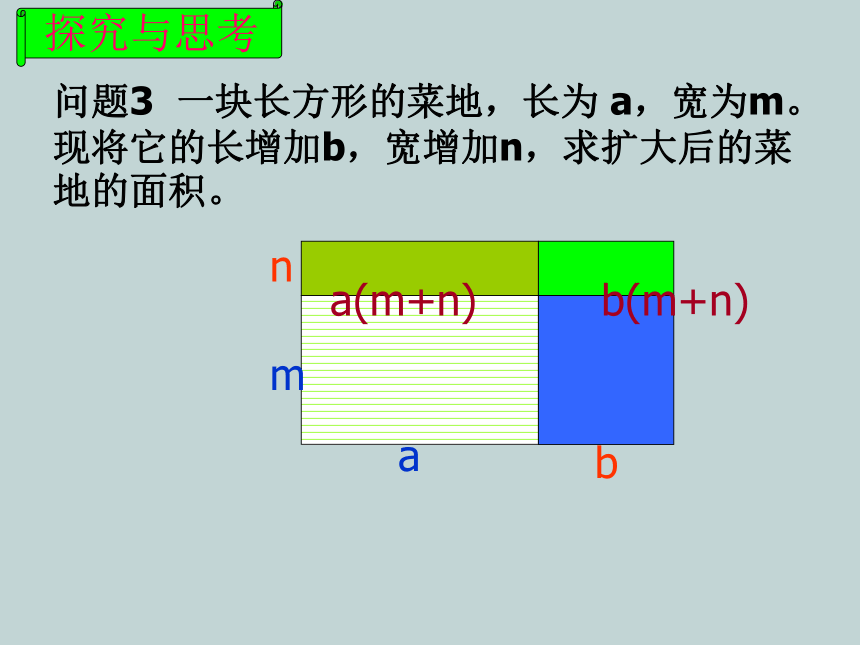
问题3 一块长方形的菜地, 长为 a,宽为m现将它的长增加b,宽增加n。求扩大后的菜地的面积。
n
b
m
a
探究与思考
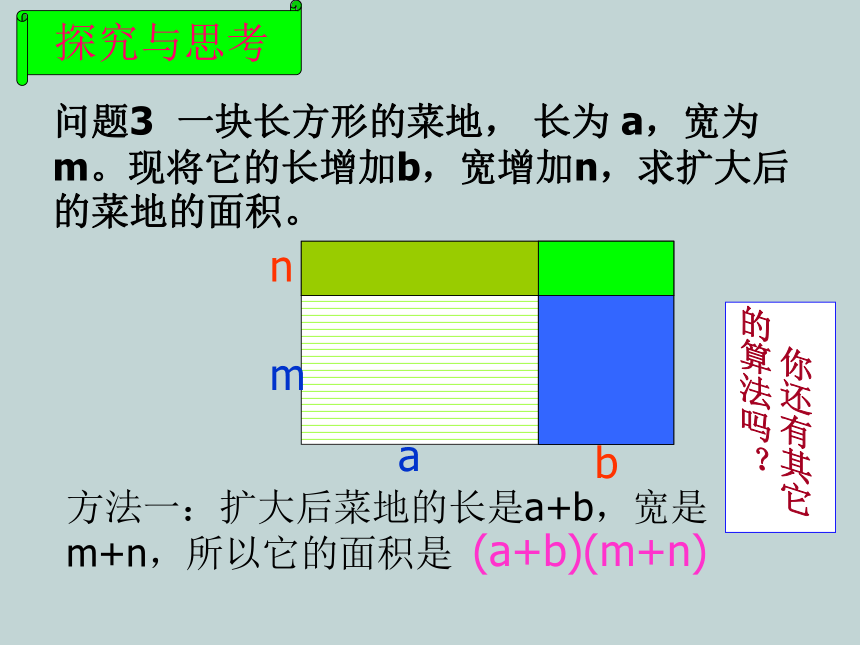
问题3 一块长方形的菜地, 长为 a,宽为m;现将它的长增加b,宽增加n。求扩大后的菜地的面积。
n
b
m
a
(a+b)(m+n)
方法一:扩大后菜地的长是a+b,宽是m+n,所以它的面积是
探究与思考
1、通过实际问题情境,探究多项式与多项式相乘的法则;
2、熟练运用多项式与多项式相乘的法则,进行运算;
3、培养学生自主探究和运算的能力,增强学生应用整体思想解决问题的意识。
学习目标
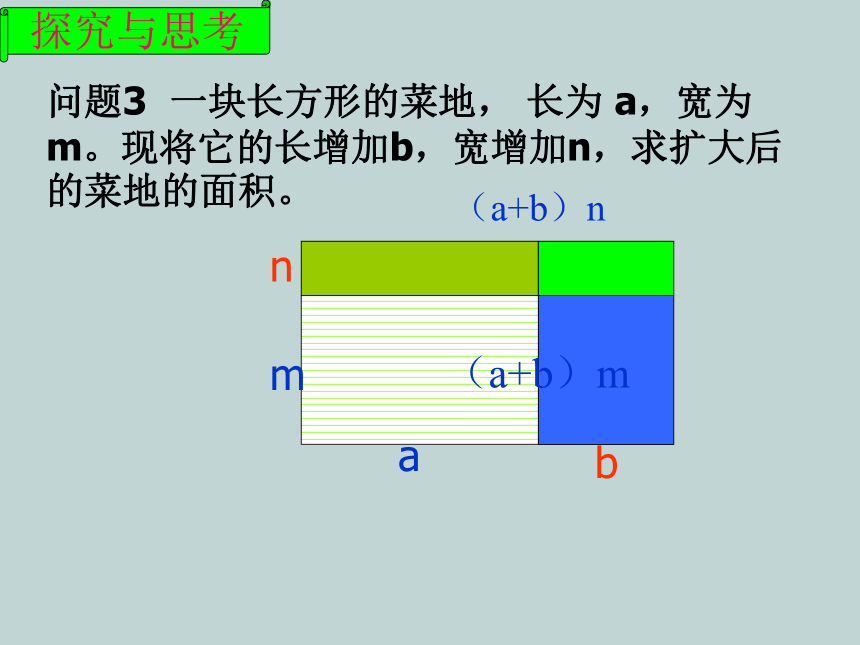
问题3 一块长方形的菜地, 长为 a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。
n
b
m
a
(a+b)(m+n)
方法一:扩大后菜地的长是a+b,宽是m+n,所以它的面积是
你还有其它的算法吗?
探究与思考
问题3 一块长方形的菜地, 长为 a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。
b
m
a
n
(a+b)m
(a+b)n
探究与思考
问题3 一块长方形的菜地,长为 a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。
n
m
a
b
a(m+n)
b(m+n)
探究与思考
问题3 一块长方形的菜地,长为 a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。
m
a
am
n
an
b
bm
bn
探究与思考
观察这几个式子:
(a+b)(m+n)
am+an+bm+bn
(a+b)m+(a+b)n
a(m+n)+b(m+n)
你能说出它们有何关系吗?
分析与比较
可以发现:
(a+b)(m+n)
am+an+bm+bn
(a+b)m+(a+b)n
a(m+n)+b(m+n)
由此你能得到什么启发?
=
=
=
分析与比较
(a+b)(m+n)
3
4
1
2
am
+an
+bm
+bn
=
你能用语言描述这个规律吗?
多项式的乘法法则
多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加.
1
3
2
4
(1) (-2x-1)(3x-2)
例 计算:
合作完成
解:原式=(-2x)·3x+(-2x). (-2)+(-1).3x+(-1).(-2)
= -6x2+4x-3x+2
= -6x2+x+2
1
2
3
4
(2)(ax+1) (cx-3)
计算:
(1) (2n+6)(n–3)
(2) (3x–y)(3x+y)
(3) (2x+5)(2x+5)
试一试
1.运用多项式的乘法法则时,必须做到不重不漏.
2.多项式与多项式相乘,仍得多项式.
3.注意确定积中的每一项的符号,多项式中每一项都包含它前面的符号,“同号得正,异号得负”.
4.多项式与多项式相乘的展开式中,有同类项要合并同类项.
温馨提示
计算:
(2) (a+b)(a2-ab+b2)
(1) (x+a)(2x-b)
挑战一下
(3) (y2+y+1)(y+2)
1. 看谁算得快又准:
(1) (2a+3b)(2a-3b)
(2) (xy–z)(xy+z)
(3) (x–1)(x2+x+1)
2.先化简再求值: (3a–2)(a+1)+(a-1)(a+3)其中a=2.
你还有什么困惑吗?
作业:
习题 8.2
P65 第4题
8.2.3多项式与多项式相乘
(1)(-3x3y)(-5x4y2z4)=_______;
(2)3a(4a-3ab-2)
=________________
15x7y3z4
12a2
-9a2b
-6a
动手算一算
1、单项式乘以单项式的法则?
思考并回答
2、单项式乘以多项式的法则?
单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。
单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加。
问题3 一块长方形的菜地, 长为 a,宽为m现将它的长增加b,宽增加n。求扩大后的菜地的面积。
n
b
m
a
探究与思考
问题3 一块长方形的菜地, 长为 a,宽为m;现将它的长增加b,宽增加n。求扩大后的菜地的面积。
n
b
m
a
(a+b)(m+n)
方法一:扩大后菜地的长是a+b,宽是m+n,所以它的面积是
探究与思考
1、通过实际问题情境,探究多项式与多项式相乘的法则;
2、熟练运用多项式与多项式相乘的法则,进行运算;
3、培养学生自主探究和运算的能力,增强学生应用整体思想解决问题的意识。
学习目标
问题3 一块长方形的菜地, 长为 a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。
n
b
m
a
(a+b)(m+n)
方法一:扩大后菜地的长是a+b,宽是m+n,所以它的面积是
你还有其它的算法吗?
探究与思考
问题3 一块长方形的菜地, 长为 a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。
b
m
a
n
(a+b)m
(a+b)n
探究与思考
问题3 一块长方形的菜地,长为 a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。
n
m
a
b
a(m+n)
b(m+n)
探究与思考
问题3 一块长方形的菜地,长为 a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。
m
a
am
n
an
b
bm
bn
探究与思考
观察这几个式子:
(a+b)(m+n)
am+an+bm+bn
(a+b)m+(a+b)n
a(m+n)+b(m+n)
你能说出它们有何关系吗?
分析与比较
可以发现:
(a+b)(m+n)
am+an+bm+bn
(a+b)m+(a+b)n
a(m+n)+b(m+n)
由此你能得到什么启发?
=
=
=
分析与比较
(a+b)(m+n)
3
4
1
2
am
+an
+bm
+bn
=
你能用语言描述这个规律吗?
多项式的乘法法则
多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加.
1
3
2
4
(1) (-2x-1)(3x-2)
例 计算:
合作完成
解:原式=(-2x)·3x+(-2x). (-2)+(-1).3x+(-1).(-2)
= -6x2+4x-3x+2
= -6x2+x+2
1
2
3
4
(2)(ax+1) (cx-3)
计算:
(1) (2n+6)(n–3)
(2) (3x–y)(3x+y)
(3) (2x+5)(2x+5)
试一试
1.运用多项式的乘法法则时,必须做到不重不漏.
2.多项式与多项式相乘,仍得多项式.
3.注意确定积中的每一项的符号,多项式中每一项都包含它前面的符号,“同号得正,异号得负”.
4.多项式与多项式相乘的展开式中,有同类项要合并同类项.
温馨提示
计算:
(2) (a+b)(a2-ab+b2)
(1) (x+a)(2x-b)
挑战一下
(3) (y2+y+1)(y+2)
1. 看谁算得快又准:
(1) (2a+3b)(2a-3b)
(2) (xy–z)(xy+z)
(3) (x–1)(x2+x+1)
2.先化简再求值: (3a–2)(a+1)+(a-1)(a+3)其中a=2.
你还有什么困惑吗?
作业:
习题 8.2
P65 第4题
