人教A版(2019)必修第二册9.2用样本估计总体同步练习(Word含答案解析)
文档属性
| 名称 | 人教A版(2019)必修第二册9.2用样本估计总体同步练习(Word含答案解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 881.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-01 00:00:00 | ||
图片预览


文档简介
人教A版(2019)必修第二册 9.2 用样本估计总体 同步练习
一、单选题
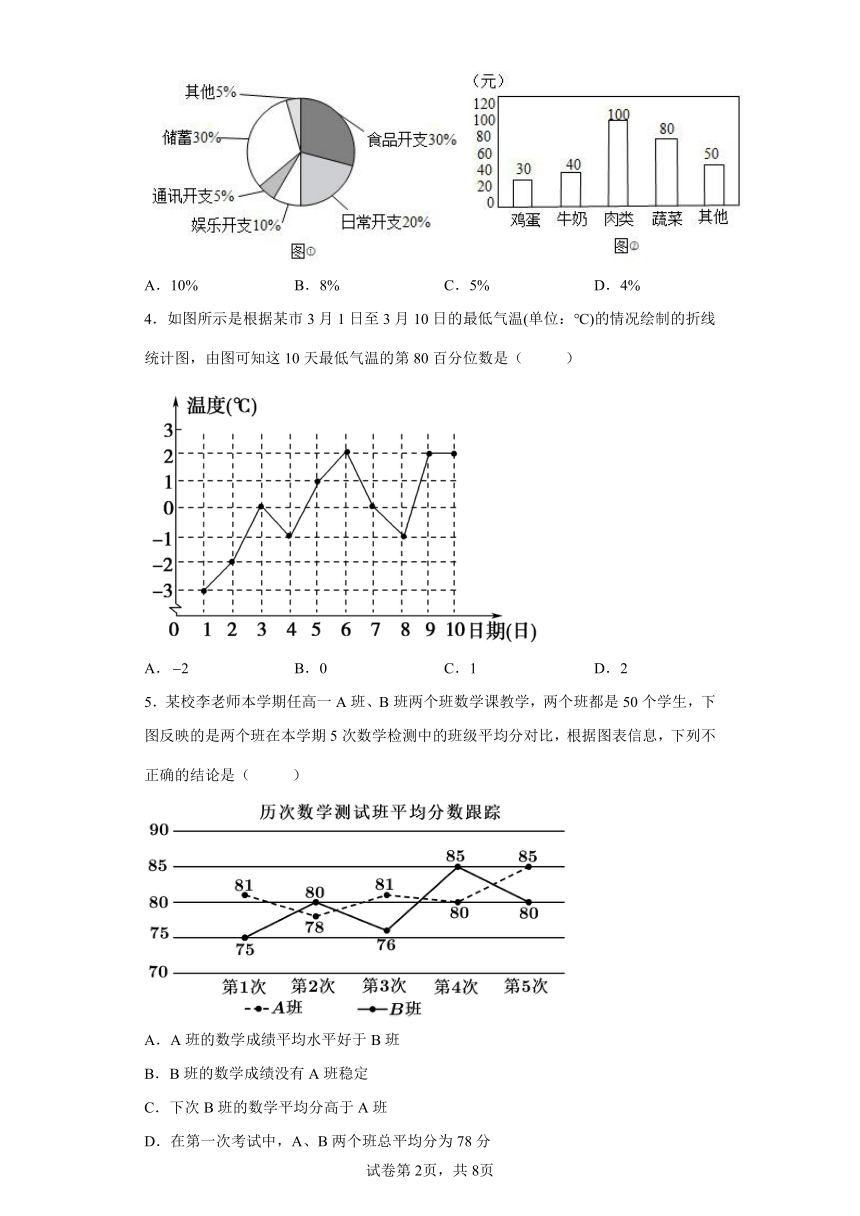
1.某工厂一年中各月份的收入、支出情况的统计如图所示,下列说法中错误的是( )
A.收入最高值与收入最低值的比是
B.结余最高的月份是7月
C.1至2月份的收入的变化率与4至5月份的收入的变化率相同
D.前6个月的平均收入为40万元
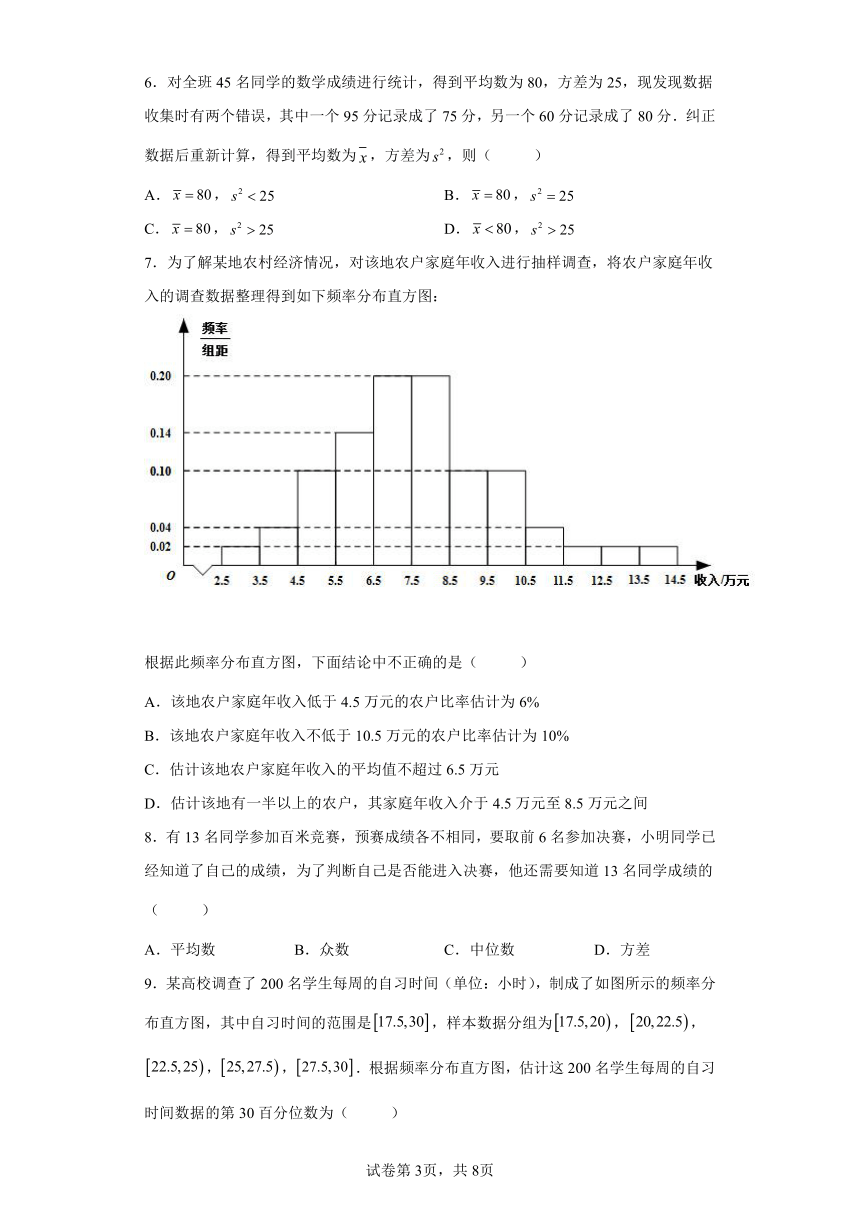
2.为了解户籍性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为100的调查样本,其中城镇户籍与农村户籍各50人;男性60人,女性40人,绘制不同群体中倾向选择生育二胎与选择不生育二胎的人数比例图(如图所示),其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
A.是否倾向选择生育二胎与户籍无关
B.是否倾向选择生育二胎与性别无关
C.倾向选择生育二胎的人员中,男性人数与女性人数相同
D.倾向选择不生育二胎的人员中,农村户籍人数少于城镇户籍人数
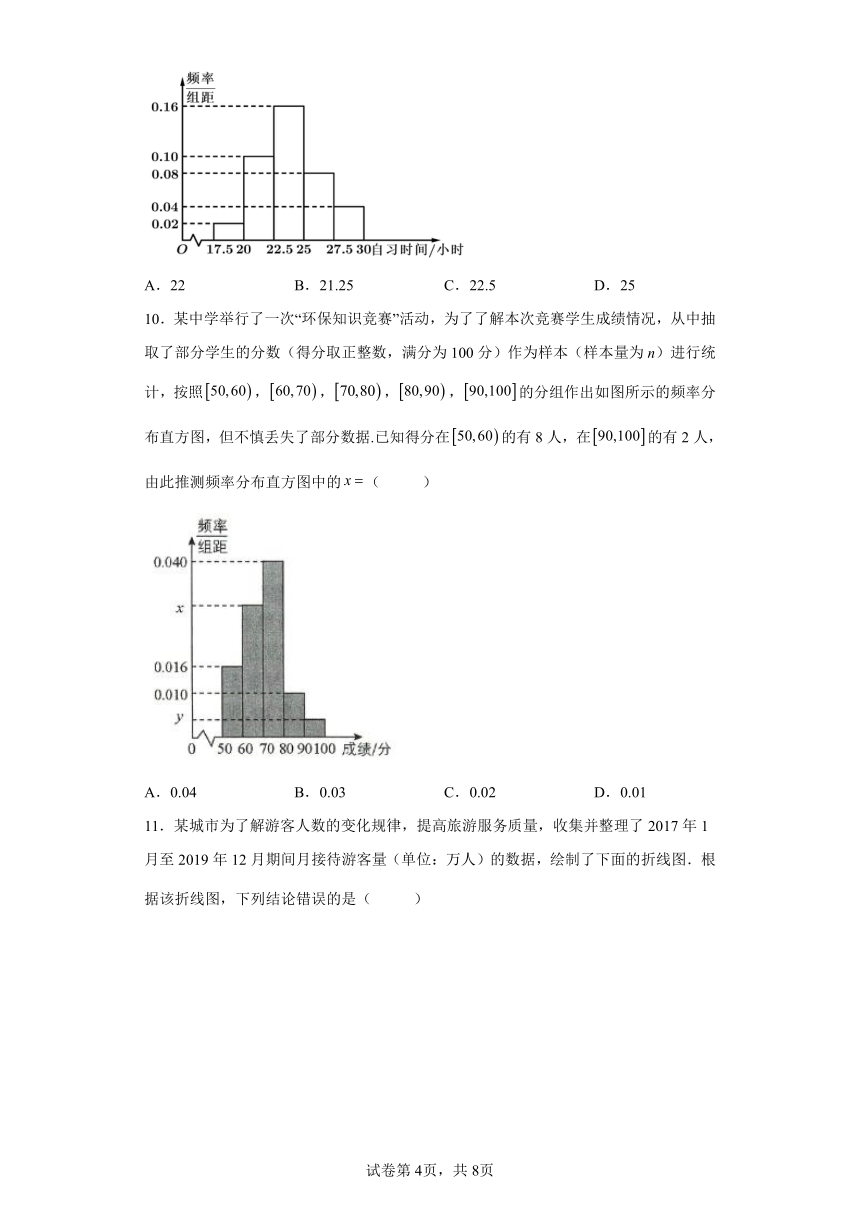
3.某学生一星期的总开支分布如图①所示,一星期的食品开支如图②所示,则该生一星期的牛奶开支占总开支的百分比约为( )
A.10% B.8% C.5% D.4%
4.如图所示是根据某市3月1日至3月10日的最低气温(单位:℃)的情况绘制的折线统计图,由图可知这10天最低气温的第80百分位数是( )
A. B.0 C.1 D.2
5.某校李老师本学期任高一A班、B班两个班数学课教学,两个班都是50个学生,下图反映的是两个班在本学期5次数学检测中的班级平均分对比,根据图表信息,下列不正确的结论是( )
A.A班的数学成绩平均水平好于B班
B.B班的数学成绩没有A班稳定
C.下次B班的数学平均分高于A班
D.在第一次考试中,A、B两个班总平均分为78分
6.对全班45名同学的数学成绩进行统计,得到平均数为80,方差为25,现发现数据收集时有两个错误,其中一个95分记录成了75分,另一个60分记录成了80分.纠正数据后重新计算,得到平均数为,方差为,则( )
A., B.,
C., D.,
7.为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
8.有13名同学参加百米竞赛,预赛成绩各不相同,要取前6名参加决赛,小明同学已经知道了自己的成绩,为了判断自己是否能进入决赛,他还需要知道13名同学成绩的( )
A.平均数 B.众数 C.中位数 D.方差
9.某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是,样本数据分组为,,,,.根据频率分布直方图,估计这200名学生每周的自习时间数据的第30百分位数为( )
A.22 B.21.25 C.22.5 D.25
10.某中学举行了一次“环保知识竞赛”活动,为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本量为n)进行统计,按照,,,,的分组作出如图所示的频率分布直方图,但不慎丢失了部分数据.已知得分在的有8人,在的有2人,由此推测频率分布直方图中的( )
A.0.04 B.0.03 C.0.02 D.0.01
11.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位数为30万人
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
12.已知样本,,,,的平均数为,样本,,,的平均数为(),若样本,,,,,,,的平均数,其中,则n,m的大小关系为( )
A. B. C. D.不能确定
13.某班数学课代表统计一次数学测验的平均分与方差,计算完毕才发现忘记把自己的分数录入进去了,只好重算一次.已知原平均分和原方差分别为,s2,新平均分和新方差分别为,,若此同学的得分恰好为,则( )
A., B.,
C., D.,
14.已知一组数据,,的平均数是5,方差是4则由,,,11这4个数据组成的新的一组数据的方差是( )
A.16 B.14 C.12 D.8
15.在成都市“高三第一次诊断性”考试后,各班级都有外出学习艺体的同学回归校园学习文化课.假设某位回归校园的同学的“一诊”数学成绩刚好是班级平均分,则对该班级的数学成绩,下列说法正确的是( )
A.平均分变大,方差不变 B.平均分变小,方差不变
C.平均分不变,方差变大 D.平均分不变,方差变小
二、填空题
16.某中学有初中学生1800人,高中学生1200人.为了解学生本学期课外阅读情况,现采用分层随机抽样的方法,从中抽取了100名学生,先统计了他们的课外阅读时间,然后按初中学生和高中学生分为两组,再将每组学生的阅读时间(单位:h)分为5组:, ,,, ,并分别加以统计,得到如图所示的频率分布直方图,试估计该校所有学生中,阅读时间不小于30h的学生人数为 _______
17.郑州市2019年各月的平均气温(℃)数据的茎叶图如图:则这组数据的中位数是___________.
18.某社会爱心组织面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取名按年龄分组:第组,第组,第组,第组,第组,得到的频率分布直方图如图所示.若从第,,组中用分层抽样的方法抽取名志愿者参与广场的宣传活动,应从第组抽取__________名志愿者.
三、解答题
19.某工厂为生产一种标准长度为的精密器件,研发了一台生产该精密器件的车床,该精密器件的实际长度为,“长度误差”为,只要“长度误差”不超过就认为合格.已知这台车床分昼、夜两个独立批次生产,每天每批次各生产件.已知每件产品的成本为元,每件合格品的利润为元.在昼、夜两个批次生产的产品中分别随机抽取件,检测其长度并绘制了如下茎叶图:
(1)分别估计在昼、夜两个批次的产品中随机抽取一件产品为合格品的概率;
(2)以上述样本的频率作为概率,求这台车床一天的总利润的平均值.
20.生产过程中,测得纤维产品的纤度(表示纤细的一种量),共有100个数据,将数据分组如下表:
分组 频数 频率
4
25
30
29
10
2
合计 100
(1)完成频率分布表,并画出频率分布直方图;
(2)估计纤度落在内的可能性及纤度小于的可能性各是多少?
21.某生物研究小组准备探究某种蜻蜒的翼长分布规律,随机捕捉20只该种蜻蜓,测量它们的翼长(翼长为整数,单位:mm)并绘制成如下的茎叶图和一部分频率分布直方图,其中基叶图中有一处数字看不清(用表示),但已知茎叶图中每一行的数据都按照从小到大的顺序排列且无相同数据频率分布直方图每个分组含左端点不含右端点.
(1)求的值;
(2)根据茎叶图将频率分布直方图补充完整;
(3)分别根据茎叶图和频率分布直方图计算蜻蜓翼长的中位数,并分析哪个中位数可以更准确地反映蜻蜓翼长的总体情况.
22.某部门在十一月份对城市居民进行了主题为空气质量问卷调查,根据每份调查表得到每个调查对象的空气质量评分值(百分制).现从收到的调查表中随机抽取20份进行统计,得到如图所示的频率分布表:
空气质量评分值 频数 频率
[50,60] 2
(60.70] 6
(70,80]
(80,90] 3
(90,100] 2
(1)请完成题目中的频率分布表,并补全题目中的频率分布直方图;
(2)该部门将邀请被问卷调查的部分居民参加如何提高空气质量的座谈会.在题中抽样统计的这20人中,已知空气质量评分值在区间(80,100]的5人中有2人被邀请参加座谈,求其中幸福指数评分值在区间(80,90]的仅有1人被邀请的概率.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
根据统计图对选项逐一分析,由此确定说法错误的选项.
【详解】
最高收入万元,最低收入万元,所以A正确.
结余最高的为月,结余万元,所以B正确.
根据两点连线的斜率可知,1至2月份的收入的变化率与4至5月份的收入的变化率相同,所以C正确.
前个月的平均收入为万元,所以D选项错误.
故选:D
2.C
通过阅读理解、识图,将数据进行比对,通过计算可得出C选项错误.
【详解】
由不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图知:
在A中,城镇户籍倾向选择生育二胎的比例为,农村户籍倾向选择生育二胎的比例为,是否倾向选择生育二胎与户籍有关,故A正确;
在B中,男性倾向选择生育二胎的比例为,女性倾向选择生育二胎的比例为,
是否倾向选择生育二胎与性别无关,故B正确;
在C中,男性倾向选择生育二胎的比例为,人数为人,
女性倾向选择生育二胎的比例为,人数为人,
倾向选择生育二胎的人员中,男性人数比女性人数多,故C错误;
在D中,倾向选择不生育二胎的人员中,农村户籍人数为人,城镇户籍人数为人,
倾向选择不生育二胎的人员中,农村户籍人数少于城镇户籍人数,故D正确.
故选:C.
3.D
根据图2可得牛奶开支占食品开支的比例,结合图1,即可得答案.
【详解】
由图2可得,牛奶开支占食品开支的比例为,
根据图1可得该生一星期的牛奶开支占总开支的百分比约为.
故选:D
4.D
利用百分位数的定义即可得解;
【详解】
由折线图可知,这10天的最低气温按照从小到大的顺序排列为:,,,,0,0,1,2,2,2,
因为共有10个数据,所以是整数,
则这10天最低气温的第80百分位数是.
故选:D
5.C
根据图表,分别求出A,B班的平均分以及方差,再依次分析各选项即可得答案.
【详解】
A班的5次数学测试平均分分别为81,80,81,80,85,5次的平均分,
B班的5次数学测试平均分分别为75,80,76,85,80,5次的平均分为,
A班的数学平均分好于B班,选项A正确;
由于A班的成绩都在80分附近,而B班的平均分变化很大,所以A班成绩稳定些,选项B正确;
下次考试A,B班的平均分不能预料,所以选项C错误;
在第一次考试中,总平均分为分,选项D正确.
故选:C
本题主要考查了根据图表求平均分等,属于基础题.解题的关键在于根据图表求平均数和方差时要细心,不能看错数据和用错公式.
6.C
根据数据纠正前后的数据总和不变,波动性变大,结合平均数、方差的意义分析,可得结果.
【详解】
因为,所以纠正数据前后的数据总和不变,故平均数不变;
但是,在对错误的数据进行纠正后,显然数据的波动性变大,故方差变大.
故选:C.
关键点点睛:本题的关键点是:依题意得出“数据纠正前后的总和不变,波动性变大”.
7.C
根据直方图的意义直接计算相应范围内的频率,即可判定ABD,以各组的中间值作为代表乘以相应的频率,然后求和即得到样本的平均数的估计值,也就是总体平均值的估计值,计算后即可判定C.
【详解】
因为频率直方图中的组距为1,所以各组的直方图的高度等于频率.样本频率直方图中的频率即可作为总体的相应比率的估计值.
该地农户家庭年收入低于4.5万元的农户的比率估计值为,故A正确;
该地农户家庭年收入不低于10.5万元的农户比率估计值为,故B正确;
该地农户家庭年收入介于4.5万元至8.5万元之间的比例估计值为,故D正确;
该地农户家庭年收入的平均值的估计值为(万元),超过6.5万元,故C错误.
综上,给出结论中不正确的是C.
故选:C.
本题考查利用样本频率直方图估计总体频率和平均值,属基础题,样本的频率可作为总体的频率的估计值,样本的平均值的估计值是各组的中间值乘以其相应频率然后求和所得值,可以作为总体的平均值的估计值.注意各组的频率等于.
8.C
成绩由小到大排列,能否进入决赛就看小明成绩排名是否在第7以前即可得解.
【详解】
把13名同学成绩按由大到小排列,取成绩靠前的6个成绩进入决赛,即最中间一个数之前的6个成绩进入决赛,
13个成绩按由大到小排列时,最中间一个数即是中位数.
故选:C
9.C
由频率分布直方图计算,找出累计频率值为0.3处对应的自习时间值即可.
【详解】
由频率分布直方图可知,区间在对应的频率为,区间在对应的频率为,,0.3处对应自习时间值恰为22.5,故这200名学生每周的自习时间数据的第30百分位数为22.5.
故选:C
10.B
根据频率分布直方图,先求得抽取学生的人数.
【详解】
得分在的有8人, 得分在的频率为
所以抽取中的人数为人
在的有2人,所以在的频率为,所以
∴由频率分布直方图各小矩形面积和为1,得.
解得.
故选:B.
本题考查了频率分布直方图的意义,补全频率分布直方图,属于基础题.
11.C
结合折线统计图分析数据逐一判断选项即可.
【详解】
由2017年1月至2020年12月期间月接待游客量的折线图得:
在中,年接待游客量虽然逐月波动,但总体上逐年增加,故正确;
在中,各年的月接待游客量高峰期都在8月,故正确;
在中,2017年1月至12月月接待游客量的中位数小于30万人,故错误;
在中,各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳,故正确.
故选:.
12.A
利用平均数的定义求出与与的关系式,和题干中的对比,可得:,,结合,最终求出结果
【详解】
由题意可得,,
,所以,.又,则
所以,故.
故选:A
13.C
根据平均数和方差的公式计算即可求解.
【详解】
设这个班有个学生,数据分别为,第个同学没有录入,
第一次计算时总分是,
方差是,
第二次计算时:,
方差
,
所以,,
故选:C.
14.C
根据,,的平均和方差是得出,
求出,,,11这4个数据得方差为即可得出答案.
【详解】
解:由已知得,,
则新数据的平均数为,
所以方差为
,
故选:C
15.D
依据平均数和方差的定义去判断即可解决.
【详解】
设该班原有n位同学,数学成绩记为
原平均分,
原方差
该同学回归校园后新平均分,即平均分不变.
该同学回归校园后新方差
,即方差变小.
故选:D
16.870
由分层抽样求出初中高中各被抽取的人数,再由频率分布直方图计算出频率,然后计算阅读时间不小于30h的人数,相加可得.
【详解】
由分层随机抽样,知抽取的初中生有60名,高中生有40名.因为初中学生中阅读时间不小于30h的频率为,所以该校所有的初中学生中,阅读时间不小于30h的学生人数约为,同理,高中学生中阅读时间不小于30h的频率为,故该校所有的高中学生中,阅读时间不小于30h的学生人数约为.所以该校所有学生中,阅读时间不小于30h的学生人数约为.
故答案为:870.
本题考查分层抽样,考查频率分布直方图,属于基础题.
17.####
中位数是按顺序排列好后,最中间的一个数,或最中间两个数的平均数,直接找到第六和第七个数,求出平均数即可.
【详解】
共有12组数据,第六和第七个数分别是20,21,所以中位数为
故答案为:
18.
先分别求出这3组的人数,再利用分层抽样的方法即可得出答案.
【详解】
第3组的人数为,
第4组的人数为,
第5组的人数为,
所以这三组共有60名志愿者,
所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,第三组应抽取名,
故答案为:3.
关键点点睛:该题考查的是有关频率分布直方图的识别以及分层抽样某层抽取个数的问题,正确解题的关键是掌握在抽取过程中每个个题被抽到的机会均等.
19.(1)昼、夜批次合格品概率估计值分别为、;(2)元.
(1)分别计算出昼、夜批次个样本中合格品的个数,据此可求得这两个批次中合格品的概率;
(2)分别计算出昼、夜批次件产品的利润,相加即可得出结果.
【详解】
(1)由样本数据可知,在昼批次的个样本中有个不合格品,有个合格品,合格品的比率为,因此昼批次合格品概率估计值为.
在夜批次的个样本中有个不合格品,有个合格品,合格品的比率为,因此夜批次合格品概率估计值为;
(2)昼批次合格品的概率为,不合格品的概率为,所以件产品中合格品的均值为件,不合格品的均值为件,所以利润为(元);
夜批次合格品的概率为,不合格品的概率为,所以件产品中合格品的均值为
件,不合格品的均值为件,所以利润为(元).
故这台车床一天的总利润的平均值为(元).
本题考查茎叶图的应用,考查概率与平均数的计算,考查计算能力,属于基础题.
20.(1)答案见解析;(2),.
(1)根据题意,由频率与频数的关系,计算可得各组的频率,进而可以做出频率分布表,结合分布表,进而可以做出频率分步直方图;
(2)由频率分布表可得纤度落在中的可能性,并可计算纤度小于的可能性.
【详解】
频率分布表如下:
分组 频数 频率
4
25
30
29
10
合计
频率分布直方图如图所示.
(2)利用样本估计总体,则纤度落在的可能性即为纤度落在的频率,即为.
纤度小于的可能性即为纤度小于的频率,即为.
21.(1);(2)作图见解析;(3)茎叶图,中位数为;频率分布直方图中,中位数为50;答案见解析.
(1)先计算出区间中的个体数,然后根据茎叶图分析的取值;
(2)根据茎叶图分别计算,,,,对应的频率除以组距的值,由此可补充频率分布直方图;
(3)茎叶图:取第个和第数据相加然后除以即可得到结果;频率分布直方图:计算频率和为时对应的横坐标的值即为中位数;然后根据茎叶图、频率分布直方图对数据的保存特点分析哪一个统计图的中位数更准确地反映蜻蜓翼长的总体情况.
【详解】
解:(1)区间对应的个体个数为,对应的三个数据分别为41,42,43,
因此必须要大于4且小于6,从而.
(2)区间,,,,对应的纵坐标分别为
,,,,.
所以频率分布直方图如下:
(3)根据茎叶图,中位数为.
频率分布直方图中,区间的频率为,因此中位数为50.
利用茎叶图计算的中位数更加准确,因为频率分布直方图损失了样本的部分信息,数据的分组对数字特征的估计结果也有影响;
茎叶图是原始数据,记录了样本的全部信息,所以能更准确地反映蜻蜓翼长的总体情况.
22.(1)见解析(2).
(1)由共20份抽样,计算可得[70,80)的频数,可得其频率,计算各区间的频率,可得补全题目中的频率分布直方图;
(2)可计算出空气质量评分值在区间(80,100]的5人中有2人被邀请参加座谈的基本事件总数,同时计算出幸福指数评分值在区间(80,90]的仅有1人被邀请包含的基本事件个数,由古典概形几率计算公式计算可得答案.
【详解】
(1)由题设条件得:
[70,80)的频数为:20﹣2﹣6﹣3﹣2=7,
∴[70,80)的频率为0.35,
完成完成题目中的频率分布表如下:
空气质量评分值 频数 频率
[50,60] 2 0.1
(60.70] 6 0.3
(70,80] 7 0.35
(80,90] 3 0.15
(90,100] 2 0.1
补全频率分布直方图,得:
(2)空气质量评分值在区间(80,100]的5人中有2人被邀请参加座谈,
基本事件总数n10,
其中幸福指数评分值在区间(80,90]的仅有1人被邀请包含的基本事件个数m6,
∴其中幸福指数评分值在区间(80,90]的仅有1人被邀请的概率p.
本题主要考查列举法计算基本事件及事件发生的概率,涉及频率分布表和频率分布直方图的应用,属于基础题.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.某工厂一年中各月份的收入、支出情况的统计如图所示,下列说法中错误的是( )
A.收入最高值与收入最低值的比是
B.结余最高的月份是7月
C.1至2月份的收入的变化率与4至5月份的收入的变化率相同
D.前6个月的平均收入为40万元
2.为了解户籍性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为100的调查样本,其中城镇户籍与农村户籍各50人;男性60人,女性40人,绘制不同群体中倾向选择生育二胎与选择不生育二胎的人数比例图(如图所示),其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
A.是否倾向选择生育二胎与户籍无关
B.是否倾向选择生育二胎与性别无关
C.倾向选择生育二胎的人员中,男性人数与女性人数相同
D.倾向选择不生育二胎的人员中,农村户籍人数少于城镇户籍人数
3.某学生一星期的总开支分布如图①所示,一星期的食品开支如图②所示,则该生一星期的牛奶开支占总开支的百分比约为( )
A.10% B.8% C.5% D.4%
4.如图所示是根据某市3月1日至3月10日的最低气温(单位:℃)的情况绘制的折线统计图,由图可知这10天最低气温的第80百分位数是( )
A. B.0 C.1 D.2
5.某校李老师本学期任高一A班、B班两个班数学课教学,两个班都是50个学生,下图反映的是两个班在本学期5次数学检测中的班级平均分对比,根据图表信息,下列不正确的结论是( )
A.A班的数学成绩平均水平好于B班
B.B班的数学成绩没有A班稳定
C.下次B班的数学平均分高于A班
D.在第一次考试中,A、B两个班总平均分为78分
6.对全班45名同学的数学成绩进行统计,得到平均数为80,方差为25,现发现数据收集时有两个错误,其中一个95分记录成了75分,另一个60分记录成了80分.纠正数据后重新计算,得到平均数为,方差为,则( )
A., B.,
C., D.,
7.为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
8.有13名同学参加百米竞赛,预赛成绩各不相同,要取前6名参加决赛,小明同学已经知道了自己的成绩,为了判断自己是否能进入决赛,他还需要知道13名同学成绩的( )
A.平均数 B.众数 C.中位数 D.方差
9.某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是,样本数据分组为,,,,.根据频率分布直方图,估计这200名学生每周的自习时间数据的第30百分位数为( )
A.22 B.21.25 C.22.5 D.25
10.某中学举行了一次“环保知识竞赛”活动,为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本量为n)进行统计,按照,,,,的分组作出如图所示的频率分布直方图,但不慎丢失了部分数据.已知得分在的有8人,在的有2人,由此推测频率分布直方图中的( )
A.0.04 B.0.03 C.0.02 D.0.01
11.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位数为30万人
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
12.已知样本,,,,的平均数为,样本,,,的平均数为(),若样本,,,,,,,的平均数,其中,则n,m的大小关系为( )
A. B. C. D.不能确定
13.某班数学课代表统计一次数学测验的平均分与方差,计算完毕才发现忘记把自己的分数录入进去了,只好重算一次.已知原平均分和原方差分别为,s2,新平均分和新方差分别为,,若此同学的得分恰好为,则( )
A., B.,
C., D.,
14.已知一组数据,,的平均数是5,方差是4则由,,,11这4个数据组成的新的一组数据的方差是( )
A.16 B.14 C.12 D.8
15.在成都市“高三第一次诊断性”考试后,各班级都有外出学习艺体的同学回归校园学习文化课.假设某位回归校园的同学的“一诊”数学成绩刚好是班级平均分,则对该班级的数学成绩,下列说法正确的是( )
A.平均分变大,方差不变 B.平均分变小,方差不变
C.平均分不变,方差变大 D.平均分不变,方差变小
二、填空题
16.某中学有初中学生1800人,高中学生1200人.为了解学生本学期课外阅读情况,现采用分层随机抽样的方法,从中抽取了100名学生,先统计了他们的课外阅读时间,然后按初中学生和高中学生分为两组,再将每组学生的阅读时间(单位:h)分为5组:, ,,, ,并分别加以统计,得到如图所示的频率分布直方图,试估计该校所有学生中,阅读时间不小于30h的学生人数为 _______
17.郑州市2019年各月的平均气温(℃)数据的茎叶图如图:则这组数据的中位数是___________.
18.某社会爱心组织面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取名按年龄分组:第组,第组,第组,第组,第组,得到的频率分布直方图如图所示.若从第,,组中用分层抽样的方法抽取名志愿者参与广场的宣传活动,应从第组抽取__________名志愿者.
三、解答题
19.某工厂为生产一种标准长度为的精密器件,研发了一台生产该精密器件的车床,该精密器件的实际长度为,“长度误差”为,只要“长度误差”不超过就认为合格.已知这台车床分昼、夜两个独立批次生产,每天每批次各生产件.已知每件产品的成本为元,每件合格品的利润为元.在昼、夜两个批次生产的产品中分别随机抽取件,检测其长度并绘制了如下茎叶图:
(1)分别估计在昼、夜两个批次的产品中随机抽取一件产品为合格品的概率;
(2)以上述样本的频率作为概率,求这台车床一天的总利润的平均值.
20.生产过程中,测得纤维产品的纤度(表示纤细的一种量),共有100个数据,将数据分组如下表:
分组 频数 频率
4
25
30
29
10
2
合计 100
(1)完成频率分布表,并画出频率分布直方图;
(2)估计纤度落在内的可能性及纤度小于的可能性各是多少?
21.某生物研究小组准备探究某种蜻蜒的翼长分布规律,随机捕捉20只该种蜻蜓,测量它们的翼长(翼长为整数,单位:mm)并绘制成如下的茎叶图和一部分频率分布直方图,其中基叶图中有一处数字看不清(用表示),但已知茎叶图中每一行的数据都按照从小到大的顺序排列且无相同数据频率分布直方图每个分组含左端点不含右端点.
(1)求的值;
(2)根据茎叶图将频率分布直方图补充完整;
(3)分别根据茎叶图和频率分布直方图计算蜻蜓翼长的中位数,并分析哪个中位数可以更准确地反映蜻蜓翼长的总体情况.
22.某部门在十一月份对城市居民进行了主题为空气质量问卷调查,根据每份调查表得到每个调查对象的空气质量评分值(百分制).现从收到的调查表中随机抽取20份进行统计,得到如图所示的频率分布表:
空气质量评分值 频数 频率
[50,60] 2
(60.70] 6
(70,80]
(80,90] 3
(90,100] 2
(1)请完成题目中的频率分布表,并补全题目中的频率分布直方图;
(2)该部门将邀请被问卷调查的部分居民参加如何提高空气质量的座谈会.在题中抽样统计的这20人中,已知空气质量评分值在区间(80,100]的5人中有2人被邀请参加座谈,求其中幸福指数评分值在区间(80,90]的仅有1人被邀请的概率.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
根据统计图对选项逐一分析,由此确定说法错误的选项.
【详解】
最高收入万元,最低收入万元,所以A正确.
结余最高的为月,结余万元,所以B正确.
根据两点连线的斜率可知,1至2月份的收入的变化率与4至5月份的收入的变化率相同,所以C正确.
前个月的平均收入为万元,所以D选项错误.
故选:D
2.C
通过阅读理解、识图,将数据进行比对,通过计算可得出C选项错误.
【详解】
由不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图知:
在A中,城镇户籍倾向选择生育二胎的比例为,农村户籍倾向选择生育二胎的比例为,是否倾向选择生育二胎与户籍有关,故A正确;
在B中,男性倾向选择生育二胎的比例为,女性倾向选择生育二胎的比例为,
是否倾向选择生育二胎与性别无关,故B正确;
在C中,男性倾向选择生育二胎的比例为,人数为人,
女性倾向选择生育二胎的比例为,人数为人,
倾向选择生育二胎的人员中,男性人数比女性人数多,故C错误;
在D中,倾向选择不生育二胎的人员中,农村户籍人数为人,城镇户籍人数为人,
倾向选择不生育二胎的人员中,农村户籍人数少于城镇户籍人数,故D正确.
故选:C.
3.D
根据图2可得牛奶开支占食品开支的比例,结合图1,即可得答案.
【详解】
由图2可得,牛奶开支占食品开支的比例为,
根据图1可得该生一星期的牛奶开支占总开支的百分比约为.
故选:D
4.D
利用百分位数的定义即可得解;
【详解】
由折线图可知,这10天的最低气温按照从小到大的顺序排列为:,,,,0,0,1,2,2,2,
因为共有10个数据,所以是整数,
则这10天最低气温的第80百分位数是.
故选:D
5.C
根据图表,分别求出A,B班的平均分以及方差,再依次分析各选项即可得答案.
【详解】
A班的5次数学测试平均分分别为81,80,81,80,85,5次的平均分,
B班的5次数学测试平均分分别为75,80,76,85,80,5次的平均分为,
A班的数学平均分好于B班,选项A正确;
由于A班的成绩都在80分附近,而B班的平均分变化很大,所以A班成绩稳定些,选项B正确;
下次考试A,B班的平均分不能预料,所以选项C错误;
在第一次考试中,总平均分为分,选项D正确.
故选:C
本题主要考查了根据图表求平均分等,属于基础题.解题的关键在于根据图表求平均数和方差时要细心,不能看错数据和用错公式.
6.C
根据数据纠正前后的数据总和不变,波动性变大,结合平均数、方差的意义分析,可得结果.
【详解】
因为,所以纠正数据前后的数据总和不变,故平均数不变;
但是,在对错误的数据进行纠正后,显然数据的波动性变大,故方差变大.
故选:C.
关键点点睛:本题的关键点是:依题意得出“数据纠正前后的总和不变,波动性变大”.
7.C
根据直方图的意义直接计算相应范围内的频率,即可判定ABD,以各组的中间值作为代表乘以相应的频率,然后求和即得到样本的平均数的估计值,也就是总体平均值的估计值,计算后即可判定C.
【详解】
因为频率直方图中的组距为1,所以各组的直方图的高度等于频率.样本频率直方图中的频率即可作为总体的相应比率的估计值.
该地农户家庭年收入低于4.5万元的农户的比率估计值为,故A正确;
该地农户家庭年收入不低于10.5万元的农户比率估计值为,故B正确;
该地农户家庭年收入介于4.5万元至8.5万元之间的比例估计值为,故D正确;
该地农户家庭年收入的平均值的估计值为(万元),超过6.5万元,故C错误.
综上,给出结论中不正确的是C.
故选:C.
本题考查利用样本频率直方图估计总体频率和平均值,属基础题,样本的频率可作为总体的频率的估计值,样本的平均值的估计值是各组的中间值乘以其相应频率然后求和所得值,可以作为总体的平均值的估计值.注意各组的频率等于.
8.C
成绩由小到大排列,能否进入决赛就看小明成绩排名是否在第7以前即可得解.
【详解】
把13名同学成绩按由大到小排列,取成绩靠前的6个成绩进入决赛,即最中间一个数之前的6个成绩进入决赛,
13个成绩按由大到小排列时,最中间一个数即是中位数.
故选:C
9.C
由频率分布直方图计算,找出累计频率值为0.3处对应的自习时间值即可.
【详解】
由频率分布直方图可知,区间在对应的频率为,区间在对应的频率为,,0.3处对应自习时间值恰为22.5,故这200名学生每周的自习时间数据的第30百分位数为22.5.
故选:C
10.B
根据频率分布直方图,先求得抽取学生的人数.
【详解】
得分在的有8人, 得分在的频率为
所以抽取中的人数为人
在的有2人,所以在的频率为,所以
∴由频率分布直方图各小矩形面积和为1,得.
解得.
故选:B.
本题考查了频率分布直方图的意义,补全频率分布直方图,属于基础题.
11.C
结合折线统计图分析数据逐一判断选项即可.
【详解】
由2017年1月至2020年12月期间月接待游客量的折线图得:
在中,年接待游客量虽然逐月波动,但总体上逐年增加,故正确;
在中,各年的月接待游客量高峰期都在8月,故正确;
在中,2017年1月至12月月接待游客量的中位数小于30万人,故错误;
在中,各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳,故正确.
故选:.
12.A
利用平均数的定义求出与与的关系式,和题干中的对比,可得:,,结合,最终求出结果
【详解】
由题意可得,,
,所以,.又,则
所以,故.
故选:A
13.C
根据平均数和方差的公式计算即可求解.
【详解】
设这个班有个学生,数据分别为,第个同学没有录入,
第一次计算时总分是,
方差是,
第二次计算时:,
方差
,
所以,,
故选:C.
14.C
根据,,的平均和方差是得出,
求出,,,11这4个数据得方差为即可得出答案.
【详解】
解:由已知得,,
则新数据的平均数为,
所以方差为
,
故选:C
15.D
依据平均数和方差的定义去判断即可解决.
【详解】
设该班原有n位同学,数学成绩记为
原平均分,
原方差
该同学回归校园后新平均分,即平均分不变.
该同学回归校园后新方差
,即方差变小.
故选:D
16.870
由分层抽样求出初中高中各被抽取的人数,再由频率分布直方图计算出频率,然后计算阅读时间不小于30h的人数,相加可得.
【详解】
由分层随机抽样,知抽取的初中生有60名,高中生有40名.因为初中学生中阅读时间不小于30h的频率为,所以该校所有的初中学生中,阅读时间不小于30h的学生人数约为,同理,高中学生中阅读时间不小于30h的频率为,故该校所有的高中学生中,阅读时间不小于30h的学生人数约为.所以该校所有学生中,阅读时间不小于30h的学生人数约为.
故答案为:870.
本题考查分层抽样,考查频率分布直方图,属于基础题.
17.####
中位数是按顺序排列好后,最中间的一个数,或最中间两个数的平均数,直接找到第六和第七个数,求出平均数即可.
【详解】
共有12组数据,第六和第七个数分别是20,21,所以中位数为
故答案为:
18.
先分别求出这3组的人数,再利用分层抽样的方法即可得出答案.
【详解】
第3组的人数为,
第4组的人数为,
第5组的人数为,
所以这三组共有60名志愿者,
所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,第三组应抽取名,
故答案为:3.
关键点点睛:该题考查的是有关频率分布直方图的识别以及分层抽样某层抽取个数的问题,正确解题的关键是掌握在抽取过程中每个个题被抽到的机会均等.
19.(1)昼、夜批次合格品概率估计值分别为、;(2)元.
(1)分别计算出昼、夜批次个样本中合格品的个数,据此可求得这两个批次中合格品的概率;
(2)分别计算出昼、夜批次件产品的利润,相加即可得出结果.
【详解】
(1)由样本数据可知,在昼批次的个样本中有个不合格品,有个合格品,合格品的比率为,因此昼批次合格品概率估计值为.
在夜批次的个样本中有个不合格品,有个合格品,合格品的比率为,因此夜批次合格品概率估计值为;
(2)昼批次合格品的概率为,不合格品的概率为,所以件产品中合格品的均值为件,不合格品的均值为件,所以利润为(元);
夜批次合格品的概率为,不合格品的概率为,所以件产品中合格品的均值为
件,不合格品的均值为件,所以利润为(元).
故这台车床一天的总利润的平均值为(元).
本题考查茎叶图的应用,考查概率与平均数的计算,考查计算能力,属于基础题.
20.(1)答案见解析;(2),.
(1)根据题意,由频率与频数的关系,计算可得各组的频率,进而可以做出频率分布表,结合分布表,进而可以做出频率分步直方图;
(2)由频率分布表可得纤度落在中的可能性,并可计算纤度小于的可能性.
【详解】
频率分布表如下:
分组 频数 频率
4
25
30
29
10
合计
频率分布直方图如图所示.
(2)利用样本估计总体,则纤度落在的可能性即为纤度落在的频率,即为.
纤度小于的可能性即为纤度小于的频率,即为.
21.(1);(2)作图见解析;(3)茎叶图,中位数为;频率分布直方图中,中位数为50;答案见解析.
(1)先计算出区间中的个体数,然后根据茎叶图分析的取值;
(2)根据茎叶图分别计算,,,,对应的频率除以组距的值,由此可补充频率分布直方图;
(3)茎叶图:取第个和第数据相加然后除以即可得到结果;频率分布直方图:计算频率和为时对应的横坐标的值即为中位数;然后根据茎叶图、频率分布直方图对数据的保存特点分析哪一个统计图的中位数更准确地反映蜻蜓翼长的总体情况.
【详解】
解:(1)区间对应的个体个数为,对应的三个数据分别为41,42,43,
因此必须要大于4且小于6,从而.
(2)区间,,,,对应的纵坐标分别为
,,,,.
所以频率分布直方图如下:
(3)根据茎叶图,中位数为.
频率分布直方图中,区间的频率为,因此中位数为50.
利用茎叶图计算的中位数更加准确,因为频率分布直方图损失了样本的部分信息,数据的分组对数字特征的估计结果也有影响;
茎叶图是原始数据,记录了样本的全部信息,所以能更准确地反映蜻蜓翼长的总体情况.
22.(1)见解析(2).
(1)由共20份抽样,计算可得[70,80)的频数,可得其频率,计算各区间的频率,可得补全题目中的频率分布直方图;
(2)可计算出空气质量评分值在区间(80,100]的5人中有2人被邀请参加座谈的基本事件总数,同时计算出幸福指数评分值在区间(80,90]的仅有1人被邀请包含的基本事件个数,由古典概形几率计算公式计算可得答案.
【详解】
(1)由题设条件得:
[70,80)的频数为:20﹣2﹣6﹣3﹣2=7,
∴[70,80)的频率为0.35,
完成完成题目中的频率分布表如下:
空气质量评分值 频数 频率
[50,60] 2 0.1
(60.70] 6 0.3
(70,80] 7 0.35
(80,90] 3 0.15
(90,100] 2 0.1
补全频率分布直方图,得:
(2)空气质量评分值在区间(80,100]的5人中有2人被邀请参加座谈,
基本事件总数n10,
其中幸福指数评分值在区间(80,90]的仅有1人被邀请包含的基本事件个数m6,
∴其中幸福指数评分值在区间(80,90]的仅有1人被邀请的概率p.
本题主要考查列举法计算基本事件及事件发生的概率,涉及频率分布表和频率分布直方图的应用,属于基础题.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
