5.5三角恒等变换 同步练习(Word版含解析)
文档属性
| 名称 | 5.5三角恒等变换 同步练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 601.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-01 20:48:34 | ||
图片预览

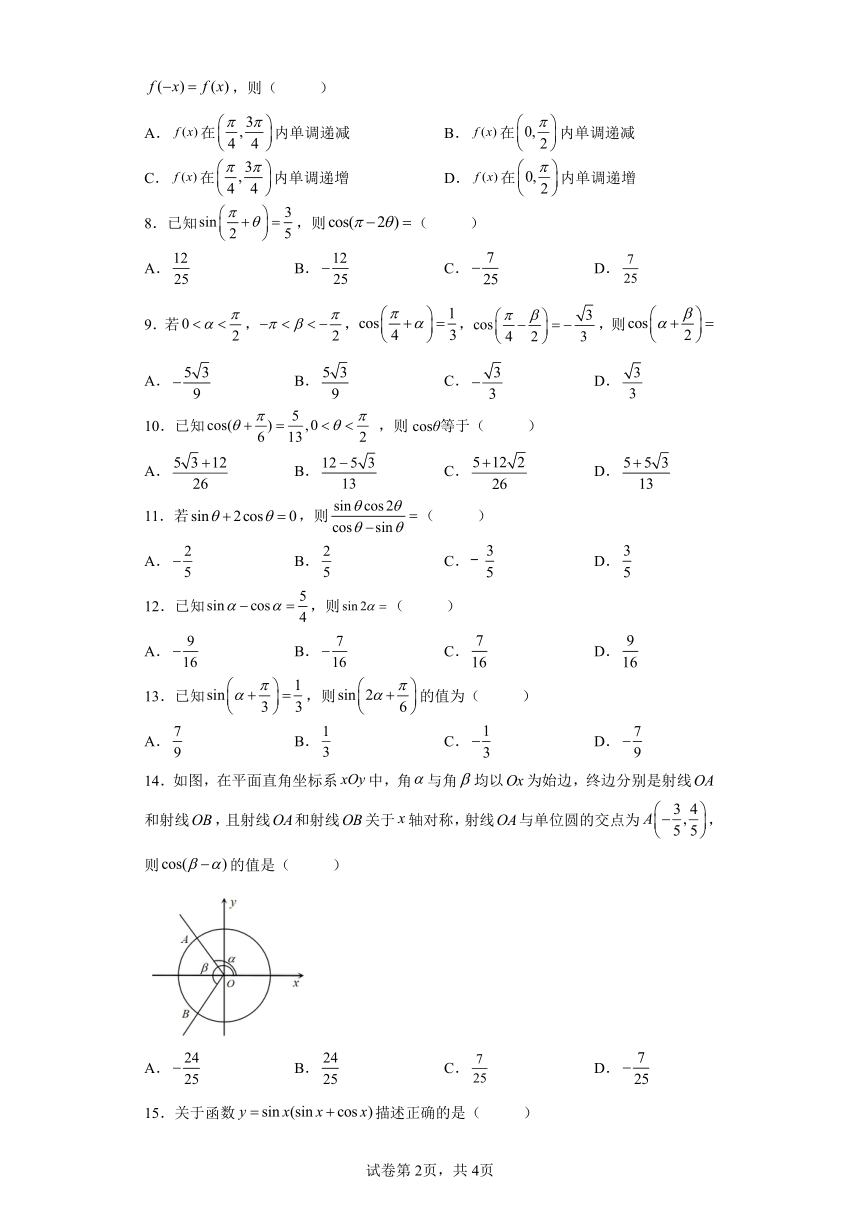


文档简介
人教A版(2019)必修第一册 5.5 三角恒等变换 同步练习
一、单选题
1.已知,,若,,则的值为( )
A. B. C. D.
2.德国著名的天文学家开普勒说过:“几何学里有两件宝,一个是勾股定理,另一个是黄金分割.如果把勾股定理比作黄金矿的话,那么可以把黄金分割比作钻石矿.”黄金三角形有两种,其中底与腰之比为黄金分割比的黄金三角形被认为是最美的三角形,它是一个顶角为的等腰三角形(另一种是顶角为的等腰三角形).例如,五角星由五个黄金三角形与一个正五边形组成,如图所示,在其中一个黄金中,.根据这些信息,可得( )
A. B. C. D.
3.已知,,、,则的值为( )
A. B.
C. D.
4.已知,,,均为锐角,则( )
A. B. C. D.
5.4( )
A.1 B. C. D.
6.化简-sin(x+y)sin(x-y)-cos(x+y)cos(x-y)的结果为( )
A.sin 2x B.cos 2x
C.-cos 2x D.-cos 2y
7.已知函数的最小正周期为,且,则( )
A.在内单调递减 B.在内单调递减
C.在内单调递增 D.在内单调递增
8.已知,则( )
A. B. C. D.
9.若,,,,则
A. B. C. D.
10.已知,则cosθ等于( )
A. B. C. D.
11.若,则( )
A. B. C. D.
12.已知,则( )
A. B. C. D.
13.已知,则的值为( )
A. B. C. D.
14.如图,在平面直角坐标系中,角与角均以为始边,终边分别是射线和射线,且射线和射线关于轴对称,射线与单位圆的交点为,则的值是( )
A. B. C. D.
15.关于函数描述正确的是( )
A.最小正周期是 B.最大值是
C.一条对称轴是 D.一个对称中心是
二、填空题
16.若,则__________
17.西气东输工程把西部的资源优势变为了经济优势,实现了气能源需求与供给的东西部衔接,同时该项工程的建设也加快了西部及沿线地区的经济发展.在输气管道工程建设过程中,某段直线形管道铺设需要经过一处平行峡谷,勘探人员在峡内恰好发现一处四分之一圆柱状的圆弧拐角,用测量仪器得到此横截圆面的圆心为,半径且为米,而运输人员利用运输工具水平横向移动直线形输气管不可避免的要经过此圆弧拐角,需从宽为米的峡谷拐入宽为米的峡谷.如图所示,位于峡谷悬崖壁上的两点,的连线恰好与圆弧拐角相切于点(点,,在同一水平面内),若要使得直线形输气管能够顺利地通过圆弧拐角,其长度不能超过______________米.
18.利用的形式计算:__________.
三、解答题
19.已知.
(1)求的值;
(2)求的值.
20.已知,,,求:、.
21.已知.
(1)求;
(2)求.
22.已知.
(1)若为锐角,求的值.
(2)求的值.
试卷第1页,共3页
试卷第2页,共2页
参考答案:
1.D
由求解.
【详解】
因为,,
所以,
又,
则,,
又,
所以,
所以,
,
故选:D
2.C
计算出,然后利用二倍角公式以及诱导公式可计算得出的值,即可得出合适的选项.
【详解】
因为是顶角为的等腰三角形,所以,,
则,,
而,所以,.
故选:C.
本题考查利用二倍角公式以及诱导公式求值,考查计算能力,属于中等题.
3.A
由、的范围求出的范围,由题意,利用平方关系求出和,由两角和与差的余弦公式求出的值即可.
【详解】
解:、,,
,
,
.
.
.
故选:A.
本题考查两角和与差的余弦公式,同角三角函数的基本关系的应用,属于基础题.
4.A
首先利用同角基本关系式求和,再利用角的变换的值.
【详解】
是锐角,,,
,,且,
,,
.
故选:A
关键点点睛:本题考查角的变换求三角函数值,本题的关键是角的变换,即变形,即求的值.
5.C
本题利用二倍角公式和特殊角三角函数值,即可得到答案.
【详解】
.
故选:C.
6.D
逆用两角差的余弦公式化简即可
【详解】
解:原式=-cos[(x+y)-(x-y)]=-cos 2y,
故选:D.
7.B
根据条件中可求出函数的解析式,再判断函数在各个区间内的单调性;
【详解】
因为最小正周期为,,得
因为,所以为偶函数,所以,
而,所以
即
当,是先减再增;
当,是单调递减;
故选:B.
本题考查正弦函数的周期、奇偶性、单调性,考查函数与方程思想、转化与化归思想,考查逻辑推理能力、运算求解能力,求解时注意先求函数的解析式,再求单调性.
8.D
先根据诱导公式进行化简,然后利用二倍角的余弦公式求解出结果.
【详解】
因为,所以,
又因为,
所以,
故选:D.
9.D
利用同角三角函数的平方关系求得、的值,利用两角差的余弦公式可求得的值.
【详解】
,,则,,
,,
因此,.
故选:D.
本题考查利用两角差的余弦公式求值,考查计算能力,属于中等题.
10.A
将改写成,然后根据,展开计算即可求解出对应结果.
【详解】
因为,
又因为,所以,所以,
所以,
故选:A.
本题考查三角恒等变换的给值求值问题,解答此类问题的关键是对角进行配凑,难度一般.常见的角的关系:、、等.
11.B
由可求得 ,根据二倍角公式化简计算即可得出结果.
【详解】
,
.
故选:B
12.A
在等式两边平方,化简后可求得的值.
【详解】
,因此,.
故选:A.
13.D
先由已知求出,而,从而可求得答案
【详解】
因为,
所以,
故选:D.
14.D
由三角函数的定义可得,,,的值,再由差角的余弦公式计算即得.
【详解】
由任意角的三角函数的定义可得,,,
因,且射线和射线关于轴对称,则射线OB与单位圆的交点为,于是得,,
因此,,
所以的值是.
故选:D
15.D
利用三角恒等变换化简得解析式,再利用正弦型函数的图像和性质得出结论.
【详解】
解:由题意得:
选项A:函数的最小正周期为,故A错误;
选项B:由于,函数的最大值为,故B错误;
选项C:函数的对称轴满足,,当时,,故C错误;
选项D:令,代入函数的,故为函数的一个对称中心,故D正确;
故选:D
16.
首先利用二倍角公式求出,再利用诱导公式计算可得;
【详解】
解:因为所以,则.
因为,所以,即,故.
所以.
故答案为:.
17.75
设,则可得AB长度的表达式,利用凑“1”法,结合基本不等式,即可求得答案.
【详解】
设,其中,
延长OM,交AB于D,过B做SB垂线,交DO于G,延长ON,交AB于E,过A做SA垂线,交NO于F,如图所示:
在中,,AF=39,则,即,
在中,,,则,即,
在中, ,OT=1,所以,
又,所以,
所以=,
因为,其中,当且仅当时,等号成立,
所以
=
,
当且仅当,即时等号成立,
所以若要使得直线形输气管能够顺利地通过圆弧拐角,其长度不能超过75米.
故答案为:75.
解题的关键是根据题意,得到AB长度的表达式,难点在于需利用凑“1”法,将表达式化简成齐次式,结合基本不等式求解,考查计算化简的能力,属中档题.
18.
利用辅助角公式化简式子,再由得出结果.
【详解】
因为,所以
故答案为:.
19.(1);(2).
(1)由已知求得,再展开两角和的余弦求解;
(2)利用倍角公式求得,的值,再展开两角差的正弦求的值.
【详解】
解:(1)∵,
∴,
∴;
(2)因为,,
.
20.;
根据角的变换,,利用两角和,差公式计算求值.
【详解】
∵,∴,
又∵,,
∴,
21.(1);(2).
(1)由角的范围和同角三角函数的关系求得,再由正弦的二倍角公式求得答案;
(2)由(1)求得..再由正切的和角公式求得答案.
【详解】
解:(1)因为,所以,
则.
(2)由(1)可知.
因为,所以.
故.
本题考查同角三角函数的关系,正弦、余弦的二倍角公式,正切的和角公式,属于中档题.
22.(1)
(2)
(1)根据题意和求得,结合两角和的余弦公式计算即可;
(2)根据题意和可得,利用二倍角的正切公式求出,结合两角和的正切公式计算即可.
(1)
由,为锐角,,
得,
∴
;
(2)
由得,
则,
∴.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知,,若,,则的值为( )
A. B. C. D.
2.德国著名的天文学家开普勒说过:“几何学里有两件宝,一个是勾股定理,另一个是黄金分割.如果把勾股定理比作黄金矿的话,那么可以把黄金分割比作钻石矿.”黄金三角形有两种,其中底与腰之比为黄金分割比的黄金三角形被认为是最美的三角形,它是一个顶角为的等腰三角形(另一种是顶角为的等腰三角形).例如,五角星由五个黄金三角形与一个正五边形组成,如图所示,在其中一个黄金中,.根据这些信息,可得( )
A. B. C. D.
3.已知,,、,则的值为( )
A. B.
C. D.
4.已知,,,均为锐角,则( )
A. B. C. D.
5.4( )
A.1 B. C. D.
6.化简-sin(x+y)sin(x-y)-cos(x+y)cos(x-y)的结果为( )
A.sin 2x B.cos 2x
C.-cos 2x D.-cos 2y
7.已知函数的最小正周期为,且,则( )
A.在内单调递减 B.在内单调递减
C.在内单调递增 D.在内单调递增
8.已知,则( )
A. B. C. D.
9.若,,,,则
A. B. C. D.
10.已知,则cosθ等于( )
A. B. C. D.
11.若,则( )
A. B. C. D.
12.已知,则( )
A. B. C. D.
13.已知,则的值为( )
A. B. C. D.
14.如图,在平面直角坐标系中,角与角均以为始边,终边分别是射线和射线,且射线和射线关于轴对称,射线与单位圆的交点为,则的值是( )
A. B. C. D.
15.关于函数描述正确的是( )
A.最小正周期是 B.最大值是
C.一条对称轴是 D.一个对称中心是
二、填空题
16.若,则__________
17.西气东输工程把西部的资源优势变为了经济优势,实现了气能源需求与供给的东西部衔接,同时该项工程的建设也加快了西部及沿线地区的经济发展.在输气管道工程建设过程中,某段直线形管道铺设需要经过一处平行峡谷,勘探人员在峡内恰好发现一处四分之一圆柱状的圆弧拐角,用测量仪器得到此横截圆面的圆心为,半径且为米,而运输人员利用运输工具水平横向移动直线形输气管不可避免的要经过此圆弧拐角,需从宽为米的峡谷拐入宽为米的峡谷.如图所示,位于峡谷悬崖壁上的两点,的连线恰好与圆弧拐角相切于点(点,,在同一水平面内),若要使得直线形输气管能够顺利地通过圆弧拐角,其长度不能超过______________米.
18.利用的形式计算:__________.
三、解答题
19.已知.
(1)求的值;
(2)求的值.
20.已知,,,求:、.
21.已知.
(1)求;
(2)求.
22.已知.
(1)若为锐角,求的值.
(2)求的值.
试卷第1页,共3页
试卷第2页,共2页
参考答案:
1.D
由求解.
【详解】
因为,,
所以,
又,
则,,
又,
所以,
所以,
,
故选:D
2.C
计算出,然后利用二倍角公式以及诱导公式可计算得出的值,即可得出合适的选项.
【详解】
因为是顶角为的等腰三角形,所以,,
则,,
而,所以,.
故选:C.
本题考查利用二倍角公式以及诱导公式求值,考查计算能力,属于中等题.
3.A
由、的范围求出的范围,由题意,利用平方关系求出和,由两角和与差的余弦公式求出的值即可.
【详解】
解:、,,
,
,
.
.
.
故选:A.
本题考查两角和与差的余弦公式,同角三角函数的基本关系的应用,属于基础题.
4.A
首先利用同角基本关系式求和,再利用角的变换的值.
【详解】
是锐角,,,
,,且,
,,
.
故选:A
关键点点睛:本题考查角的变换求三角函数值,本题的关键是角的变换,即变形,即求的值.
5.C
本题利用二倍角公式和特殊角三角函数值,即可得到答案.
【详解】
.
故选:C.
6.D
逆用两角差的余弦公式化简即可
【详解】
解:原式=-cos[(x+y)-(x-y)]=-cos 2y,
故选:D.
7.B
根据条件中可求出函数的解析式,再判断函数在各个区间内的单调性;
【详解】
因为最小正周期为,,得
因为,所以为偶函数,所以,
而,所以
即
当,是先减再增;
当,是单调递减;
故选:B.
本题考查正弦函数的周期、奇偶性、单调性,考查函数与方程思想、转化与化归思想,考查逻辑推理能力、运算求解能力,求解时注意先求函数的解析式,再求单调性.
8.D
先根据诱导公式进行化简,然后利用二倍角的余弦公式求解出结果.
【详解】
因为,所以,
又因为,
所以,
故选:D.
9.D
利用同角三角函数的平方关系求得、的值,利用两角差的余弦公式可求得的值.
【详解】
,,则,,
,,
因此,.
故选:D.
本题考查利用两角差的余弦公式求值,考查计算能力,属于中等题.
10.A
将改写成,然后根据,展开计算即可求解出对应结果.
【详解】
因为,
又因为,所以,所以,
所以,
故选:A.
本题考查三角恒等变换的给值求值问题,解答此类问题的关键是对角进行配凑,难度一般.常见的角的关系:、、等.
11.B
由可求得 ,根据二倍角公式化简计算即可得出结果.
【详解】
,
.
故选:B
12.A
在等式两边平方,化简后可求得的值.
【详解】
,因此,.
故选:A.
13.D
先由已知求出,而,从而可求得答案
【详解】
因为,
所以,
故选:D.
14.D
由三角函数的定义可得,,,的值,再由差角的余弦公式计算即得.
【详解】
由任意角的三角函数的定义可得,,,
因,且射线和射线关于轴对称,则射线OB与单位圆的交点为,于是得,,
因此,,
所以的值是.
故选:D
15.D
利用三角恒等变换化简得解析式,再利用正弦型函数的图像和性质得出结论.
【详解】
解:由题意得:
选项A:函数的最小正周期为,故A错误;
选项B:由于,函数的最大值为,故B错误;
选项C:函数的对称轴满足,,当时,,故C错误;
选项D:令,代入函数的,故为函数的一个对称中心,故D正确;
故选:D
16.
首先利用二倍角公式求出,再利用诱导公式计算可得;
【详解】
解:因为所以,则.
因为,所以,即,故.
所以.
故答案为:.
17.75
设,则可得AB长度的表达式,利用凑“1”法,结合基本不等式,即可求得答案.
【详解】
设,其中,
延长OM,交AB于D,过B做SB垂线,交DO于G,延长ON,交AB于E,过A做SA垂线,交NO于F,如图所示:
在中,,AF=39,则,即,
在中,,,则,即,
在中, ,OT=1,所以,
又,所以,
所以=,
因为,其中,当且仅当时,等号成立,
所以
=
,
当且仅当,即时等号成立,
所以若要使得直线形输气管能够顺利地通过圆弧拐角,其长度不能超过75米.
故答案为:75.
解题的关键是根据题意,得到AB长度的表达式,难点在于需利用凑“1”法,将表达式化简成齐次式,结合基本不等式求解,考查计算化简的能力,属中档题.
18.
利用辅助角公式化简式子,再由得出结果.
【详解】
因为,所以
故答案为:.
19.(1);(2).
(1)由已知求得,再展开两角和的余弦求解;
(2)利用倍角公式求得,的值,再展开两角差的正弦求的值.
【详解】
解:(1)∵,
∴,
∴;
(2)因为,,
.
20.;
根据角的变换,,利用两角和,差公式计算求值.
【详解】
∵,∴,
又∵,,
∴,
21.(1);(2).
(1)由角的范围和同角三角函数的关系求得,再由正弦的二倍角公式求得答案;
(2)由(1)求得..再由正切的和角公式求得答案.
【详解】
解:(1)因为,所以,
则.
(2)由(1)可知.
因为,所以.
故.
本题考查同角三角函数的关系,正弦、余弦的二倍角公式,正切的和角公式,属于中档题.
22.(1)
(2)
(1)根据题意和求得,结合两角和的余弦公式计算即可;
(2)根据题意和可得,利用二倍角的正切公式求出,结合两角和的正切公式计算即可.
(1)
由,为锐角,,
得,
∴
;
(2)
由得,
则,
∴.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
