18.1.2平行四边形的判定 习题课 课件 2021-2022学年人教版八年级数学下册
文档属性
| 名称 | 18.1.2平行四边形的判定 习题课 课件 2021-2022学年人教版八年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 259.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 21:17:28 | ||
图片预览



文档简介
(共23张PPT)
18.1.2平行四边形的判定
习题课
第十八章 平行四边形
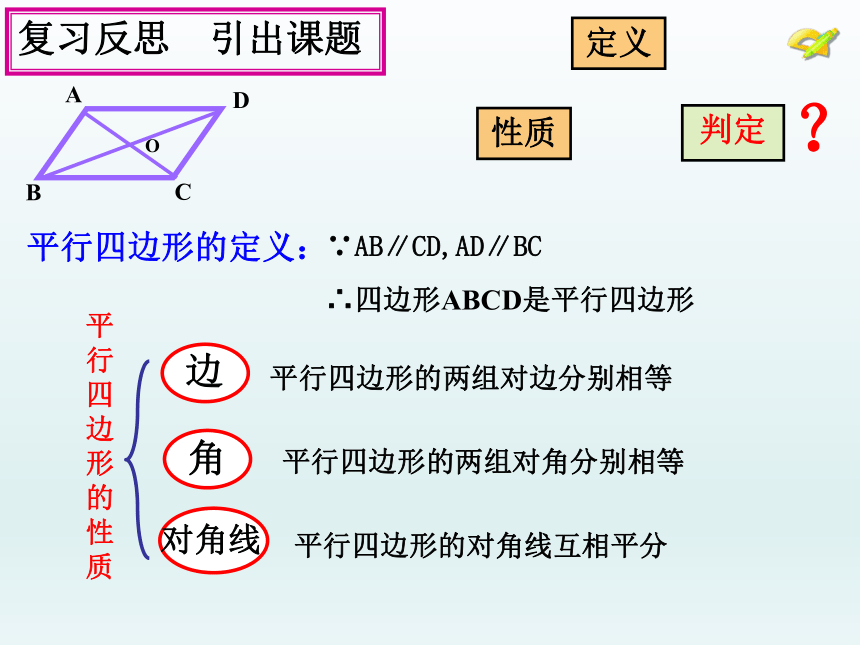
平行四边形的定义:
?
判定
性质
定义
复习反思 引出课题
B
D
A
C
O
平行四边形的性质
边
角
对角线
平行四边形的两组对边分别相等
平行四边形的两组对角分别相等
平行四边形的对角线互相平分
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
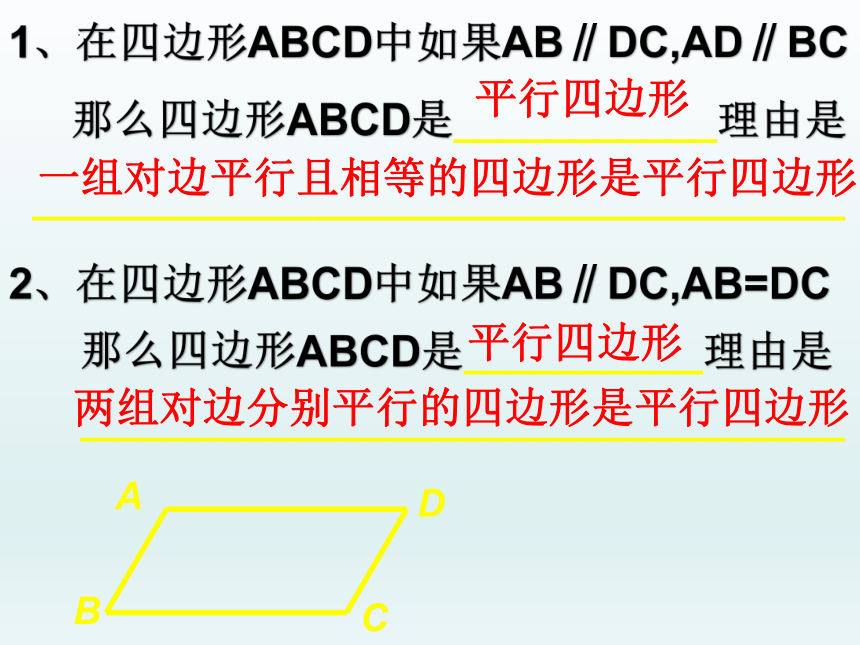
2、在四边形ABCD中如果AB∥DC,AB=DC那么四边形ABCD是__________理由是
________________________________
1、在四边形ABCD中如果AB∥DC,AD∥BC那么四边形ABCD是___________理由是
__________________________________
平行四边形
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
平行四边形
B
D
A
C
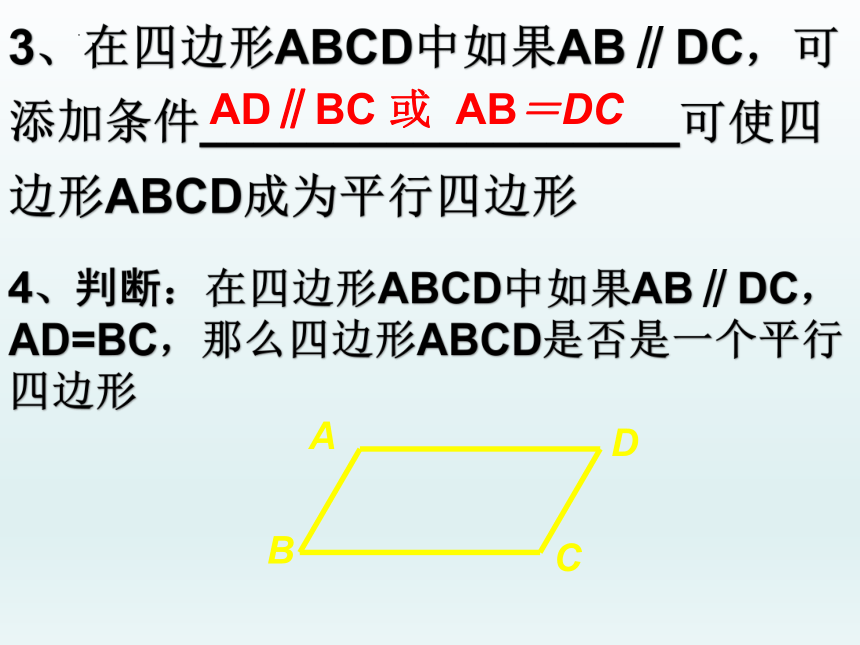
3、在四边形ABCD中如果AB∥DC,可添加条件__________________可使四边形ABCD成为平行四边形
AD∥BC
或 AB=DC
4、判断:在四边形ABCD中如果AB∥DC,AD=BC,那么四边形ABCD是否是一个平行四边形
B
D
A
C
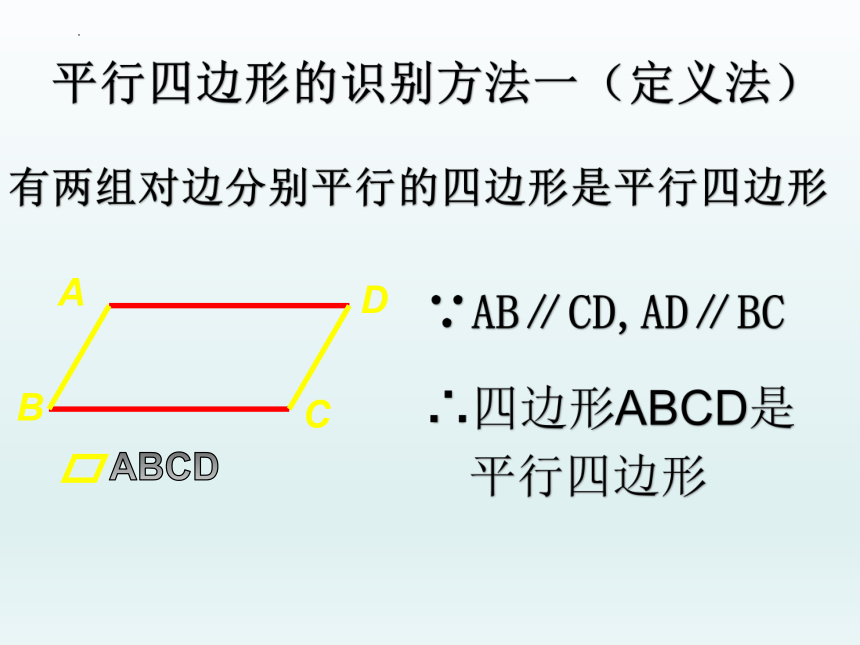
有两组对边分别平行的四边形是平行四边形
平行四边形的识别方法一(定义法)
B
D
A
C
ABCD
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
一组对边平行且相等的四边形是平行四边形
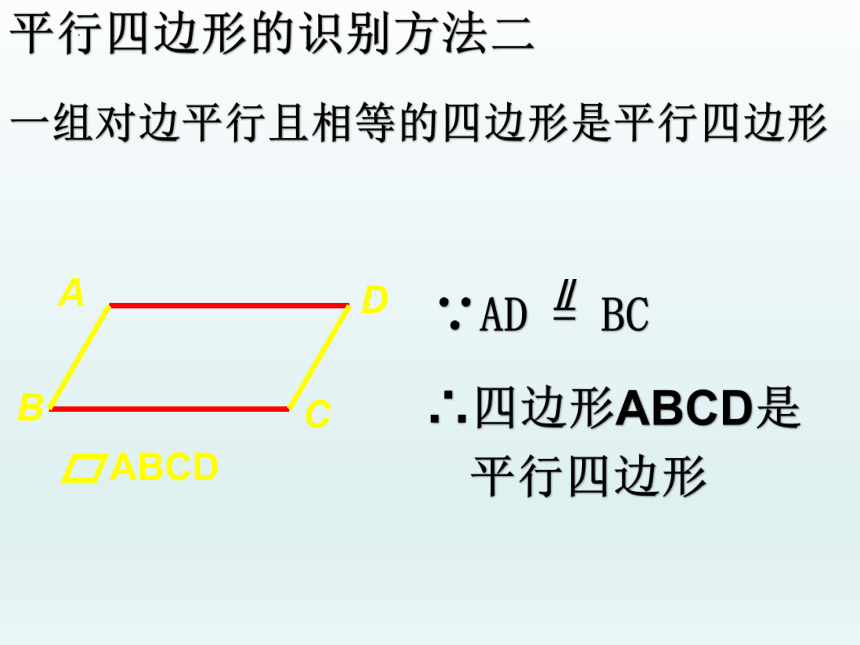
平行四边形的识别方法二
B
D
A
C
ABCD
∵AD = BC
∴四边形ABCD是平行四边形
∥
3. 如图,在 ABCD中,点E,F在对角线BD上,且BE=DF.
求证:(1)AE=CF;
(2)四边形AECF是平行四边形.
证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠ABE=∠CDF.
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS).
∴AE=CF.
(2)∵△ABE≌△DCF,
∴∠AEB=∠CFD,
∴180°-∠AEB=180°-∠CFD,
∴∠AEF=∠CFE,
∴AE∥CF,
∵AE=CF,
∴四边形AECF是平行四边形.
对角线互相平分的四边形是平行四边形
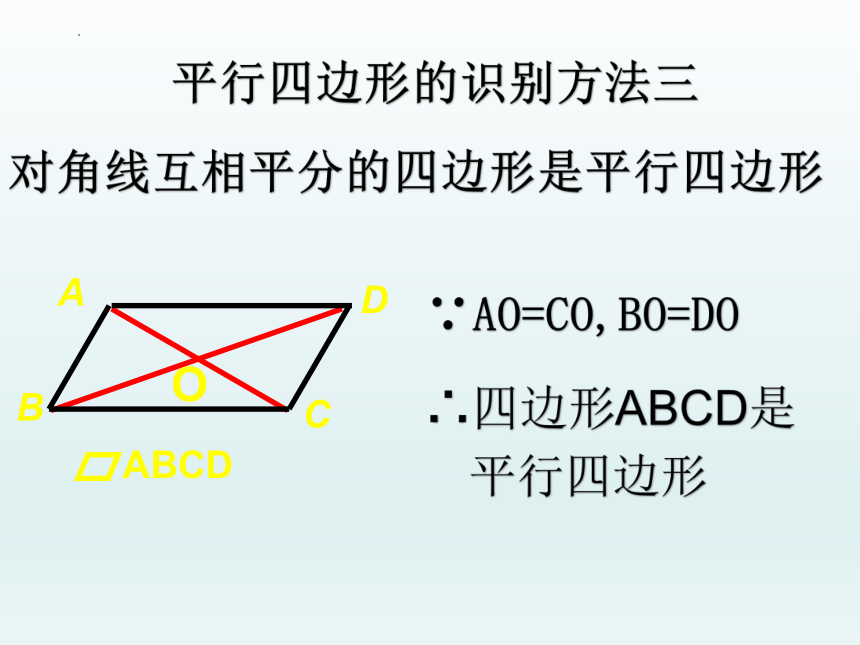
平行四边形的识别方法三
ABCD
∵AO=CO,BO=DO
∴四边形ABCD是平行四边形
B
D
A
C
O
例5. 如图,在平行四边形ABCD中,对角线AC 与BD交于点O,已知点E,F分别是AO, OC的中点;试说明: 四边形BFDE是平行四边形.
∵四边形ABCD为平行四边形
解:
∴OA=OC,OB=OD
又∵ E,F分别是AO,OC的中点
∴OE=OF
∴四边形BFDE是平行四边形.
E
F
O
两组对角分别相等的四边形是平行四边形
平行四边形的识别方法四
B
D
A
C
∵∠ A= ∠C,∠B=∠D
∴四边形ABCD是平行四边形
例6. 如左图,在四边形ABCD中,已知 ∠A=∠C,∠B=∠D试说明四边形ABCD是平行四边形.
∠A=∠C,∠B=∠D
∴∠A+∠B=1800
∴ AD∥BC
解:
∴ 四边形ABCD为平行四边形
∵∠A+∠B+∠C+∠D=3600
同理:AB∥CD
1. 下列命题中,真命题是( )
①两组对边分别相等的四边形是平行四边形
②一组对边平行,另一组对边相等的四边形是平行四边形
③两组对角分别相等的四边形是平行四边形
④对角线相等的四边形是平行四边形
A. ①② B. ①③ C. ②③ D. ③④
B
4. 如图, ABCD的对角线AC和BD相交于O,A′,B′,C′,D′分别是AO,BO,CO,DO的中点.求证:四边形A′B′C′D′是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AO=OC,BO=OD,
∵A′,C′分别是OA和CO的中点,
∴A′O= AO,C′O= CO,
∴A′O=C′O,
同理可得:B′O=D′O,
∴四边形A′B′C′D′是平行四边形.
例3.如图, □ABCD的对角线AC,BD相交于点O,E,F
是AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
证明:∵四边形ABCD是平行四边形,
∴ OA=OC,OB=OD ∵AE=CF
∴OA-AE=OC-CF
即 OE=OF
又 BO=DO
∴ 四边形BFDE是平行四边形
A
D
B
E
F
O
C
例题精讲
D
A
B
C
E
F
如图,在 □ABCD中,E,F是对角线AC上的两点,且AE=CF.
求证:∠EBF=∠FDE
变式训练
1、请你判别下列四边形哪些是平行四边形 为什么?
A
D
C
B
110°
70°
110°
⑴
⑶
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
⑵
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
7.6㎝
课堂检测
2、在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么
当BC= ___ cm, CD= ____cm时,
四边形ABCD为平行四边形;
(2)若AC=10cm,BD=18cm,那么
当AO=___ cm, DO= ____cm时,
四边形ABCD为平行四边形.
A
B
C
D
O
8㎝
4㎝
8
4
5
9
3、在□ABCD中,∠AEB=∠EDF, BE , DF分别交 AD、BC于点E、点F,
求证:四边形EBFD是平行四边形。
F
E
D
C
B
A
1、如图,在四边形ABCD中,对角线AC,BD,相交于点E,∠CBD= 90 °,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( )
E
D
C
B
A
提升训练
2、一个四边形的边长依次是a,b,c,d,且满足
,则这个四边形是
。
平行四边形
A、6 B、12
C、2 0 D、24
D
文字语言 图形语言 符号语言
A
B
C
D
A
B
C
D
O
A
B
C
D
A
B
C
D
课堂小结—知识小结
两组对边分别平行的四边形是平行四边形
(定义)
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
∵AB∥CD,
AD∥BC
∴…是平行四边形
∵OA=OC,
OB=OD
∴…是平行四边形
∵∠A=∠C,
∠B=∠D
∴…是平行四边形
∵AB=CD,
AD= BC
∴…是平行四边形
边
对角线
角
课堂小结—方法小结
解题方法
思想方法
谢谢
18.1.2平行四边形的判定
习题课
第十八章 平行四边形
平行四边形的定义:
?
判定
性质
定义
复习反思 引出课题
B
D
A
C
O
平行四边形的性质
边
角
对角线
平行四边形的两组对边分别相等
平行四边形的两组对角分别相等
平行四边形的对角线互相平分
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
2、在四边形ABCD中如果AB∥DC,AB=DC那么四边形ABCD是__________理由是
________________________________
1、在四边形ABCD中如果AB∥DC,AD∥BC那么四边形ABCD是___________理由是
__________________________________
平行四边形
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
平行四边形
B
D
A
C
3、在四边形ABCD中如果AB∥DC,可添加条件__________________可使四边形ABCD成为平行四边形
AD∥BC
或 AB=DC
4、判断:在四边形ABCD中如果AB∥DC,AD=BC,那么四边形ABCD是否是一个平行四边形
B
D
A
C
有两组对边分别平行的四边形是平行四边形
平行四边形的识别方法一(定义法)
B
D
A
C
ABCD
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
一组对边平行且相等的四边形是平行四边形
平行四边形的识别方法二
B
D
A
C
ABCD
∵AD = BC
∴四边形ABCD是平行四边形
∥
3. 如图,在 ABCD中,点E,F在对角线BD上,且BE=DF.
求证:(1)AE=CF;
(2)四边形AECF是平行四边形.
证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
∴∠ABE=∠CDF.
在△ABE和△CDF中,
∴△ABE≌△CDF(SAS).
∴AE=CF.
(2)∵△ABE≌△DCF,
∴∠AEB=∠CFD,
∴180°-∠AEB=180°-∠CFD,
∴∠AEF=∠CFE,
∴AE∥CF,
∵AE=CF,
∴四边形AECF是平行四边形.
对角线互相平分的四边形是平行四边形
平行四边形的识别方法三
ABCD
∵AO=CO,BO=DO
∴四边形ABCD是平行四边形
B
D
A
C
O
例5. 如图,在平行四边形ABCD中,对角线AC 与BD交于点O,已知点E,F分别是AO, OC的中点;试说明: 四边形BFDE是平行四边形.
∵四边形ABCD为平行四边形
解:
∴OA=OC,OB=OD
又∵ E,F分别是AO,OC的中点
∴OE=OF
∴四边形BFDE是平行四边形.
E
F
O
两组对角分别相等的四边形是平行四边形
平行四边形的识别方法四
B
D
A
C
∵∠ A= ∠C,∠B=∠D
∴四边形ABCD是平行四边形
例6. 如左图,在四边形ABCD中,已知 ∠A=∠C,∠B=∠D试说明四边形ABCD是平行四边形.
∠A=∠C,∠B=∠D
∴∠A+∠B=1800
∴ AD∥BC
解:
∴ 四边形ABCD为平行四边形
∵∠A+∠B+∠C+∠D=3600
同理:AB∥CD
1. 下列命题中,真命题是( )
①两组对边分别相等的四边形是平行四边形
②一组对边平行,另一组对边相等的四边形是平行四边形
③两组对角分别相等的四边形是平行四边形
④对角线相等的四边形是平行四边形
A. ①② B. ①③ C. ②③ D. ③④
B
4. 如图, ABCD的对角线AC和BD相交于O,A′,B′,C′,D′分别是AO,BO,CO,DO的中点.求证:四边形A′B′C′D′是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AO=OC,BO=OD,
∵A′,C′分别是OA和CO的中点,
∴A′O= AO,C′O= CO,
∴A′O=C′O,
同理可得:B′O=D′O,
∴四边形A′B′C′D′是平行四边形.
例3.如图, □ABCD的对角线AC,BD相交于点O,E,F
是AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
证明:∵四边形ABCD是平行四边形,
∴ OA=OC,OB=OD ∵AE=CF
∴OA-AE=OC-CF
即 OE=OF
又 BO=DO
∴ 四边形BFDE是平行四边形
A
D
B
E
F
O
C
例题精讲
D
A
B
C
E
F
如图,在 □ABCD中,E,F是对角线AC上的两点,且AE=CF.
求证:∠EBF=∠FDE
变式训练
1、请你判别下列四边形哪些是平行四边形 为什么?
A
D
C
B
110°
70°
110°
⑴
⑶
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
⑵
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
7.6㎝
课堂检测
2、在四边形ABCD中,AC、BD相交于点O,
(1)若AD=8cm,AB=4cm,那么
当BC= ___ cm, CD= ____cm时,
四边形ABCD为平行四边形;
(2)若AC=10cm,BD=18cm,那么
当AO=___ cm, DO= ____cm时,
四边形ABCD为平行四边形.
A
B
C
D
O
8㎝
4㎝
8
4
5
9
3、在□ABCD中,∠AEB=∠EDF, BE , DF分别交 AD、BC于点E、点F,
求证:四边形EBFD是平行四边形。
F
E
D
C
B
A
1、如图,在四边形ABCD中,对角线AC,BD,相交于点E,∠CBD= 90 °,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( )
E
D
C
B
A
提升训练
2、一个四边形的边长依次是a,b,c,d,且满足
,则这个四边形是
。
平行四边形
A、6 B、12
C、2 0 D、24
D
文字语言 图形语言 符号语言
A
B
C
D
A
B
C
D
O
A
B
C
D
A
B
C
D
课堂小结—知识小结
两组对边分别平行的四边形是平行四边形
(定义)
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
∵AB∥CD,
AD∥BC
∴…是平行四边形
∵OA=OC,
OB=OD
∴…是平行四边形
∵∠A=∠C,
∠B=∠D
∴…是平行四边形
∵AB=CD,
AD= BC
∴…是平行四边形
边
对角线
角
课堂小结—方法小结
解题方法
思想方法
谢谢
