北师大版数学八年级下册 1.1 第3课时 等腰三角形的判定与反证法-课件
文档属性
| 名称 | 北师大版数学八年级下册 1.1 第3课时 等腰三角形的判定与反证法-课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 267.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 16:09:07 | ||
图片预览




文档简介
(共16张PPT)
第一章 三角形的证明
1.1 等腰三角形
第3课时 等腰三角形的判定与反证法
核心提要
B
D
核心提要
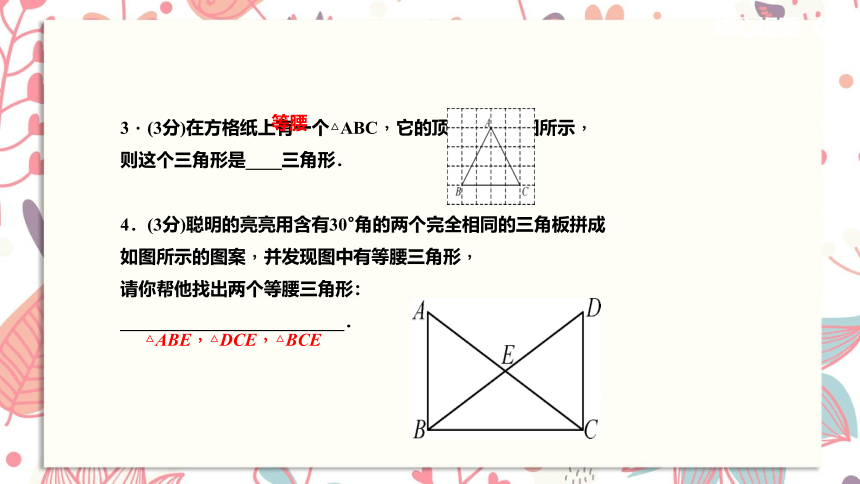
3.(3分)在方格纸上有一个△ABC,它的顶点位置如图所示,
则这个三角形是____三角形.
4.(3分)聪明的亮亮用含有30°角的两个完全相同的三角板拼成
如图所示的图案,并发现图中有等腰三角形,
请你帮他找出两个等腰三角形:
_________________________.
等腰
△ABE,△DCE,△BCE
核心提要
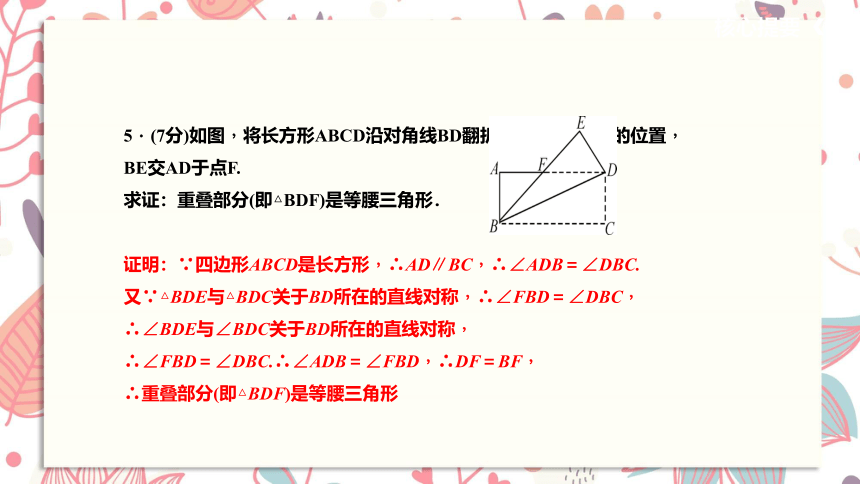
5.(7分)如图,将长方形ABCD沿对角线BD翻折,点C落在点E的位置,
BE交AD于点F.
求证:重叠部分(即△BDF)是等腰三角形.
证明:∵四边形ABCD是长方形,∴AD∥BC,∴∠ADB=∠DBC.
又∵△BDE与△BDC关于BD所在的直线对称,∴∠FBD=∠DBC,
∴∠BDE与∠BDC关于BD所在的直线对称,
∴∠FBD=∠DBC.∴∠ADB=∠FBD,∴DF=BF,
∴重叠部分(即△BDF)是等腰三角形
核心提要
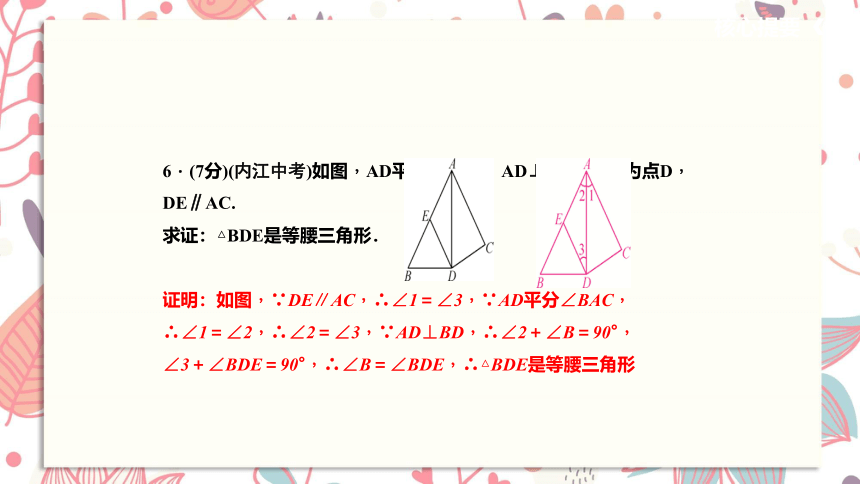
6.(7分)(内江中考)如图,AD平分∠BAC,AD⊥BD,垂足为点D,
DE∥AC.
求证:△BDE是等腰三角形.
证明:如图,∵DE∥AC,∴∠1=∠3,∵AD平分∠BAC,
∴∠1=∠2,∴∠2=∠3,∵AD⊥BD,∴∠2+∠B=90°,
∠3+∠BDE=90°,∴∠B=∠BDE,∴△BDE是等腰三角形
核心提要
C
核心提要
8.(3分)(驻马店月考)在用反证法证明命题“在一个三角形中,
至少有一个内角大于或等于60°”时,
应首先假设__________________________________.
在一个三角形中,三个内角都小于60°
核心提要
9.(8分)用反证法证明:等腰三角形的两底角必为锐角.
证明:①假设等腰三角形的底角∠B,∠C都是直角,
则_____________________,
从而____________________>180°,
这与___________________矛盾.
②设等腰三角形的底角∠B,∠C都是钝角,
则_________________,从而_________________________,
这与___________________矛盾.
综上所述,假设①,②_______________,
所以∠B,∠C只能为____.
故等腰三角形的两底角必为锐角.
∠B=∠C=90°
∠A+∠B+∠C
三角形内角和为180°
∠B+∠C>180°
∠A+∠B+∠C>180°
三角形内角和为180°
均不成立
锐角
知识点整合训练
D
知识点整合训练
11.如图所示,在△ABC中,∠ABC与∠ACB的平分线交于点O.
过O点作DE∥BC,分别交AB,AC于点D,E.若AB=5,AC=4,
则△ADE的周长是____.
12.在一次夏令营活动中,小明同学从营地A出发,
要到A地的北偏东60°方向的C处.
他先沿正东方向走了200 m到达B地,再沿北偏东30°方向走,
恰能到达目的地C,如图所示,由此可知,B,C两地相距____m.
9
200
知识点整合训练
13.(12分)如图,在△ABC中,D,E分别是AC,AB上的点,
BD与CE交于点O.给出下列四个条件:
①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
上述四个条件中,哪两个条件可判定△ABC是等腰三角形?
选择其中的一种情形,证明△ABC是等腰三角形.
知识点整合训练
知识点整合训练
14.(12分)如图所示,在四边形ABDC中,AB=AC,∠B=∠C,
求证:BD=CD.
证明:连接BC,∵AB=AC,∴∠ABC=∠ACB.
∵∠ABD=∠ACD,∴∠ABD-∠ABC=∠ACD-∠ACB,
即∠DBC=∠DCB,∴BD=CD
知识点整合训练
【综合运用】
15.(18分)如图所示,在△ABC中,已知∠ABC=∠ACB,
BO平分∠ABC,CO平分∠ACB.
(1)想想看,你能得到什么结论?
(2)若过点O作一直线EF和边BC平行,与AB交于点E,与AC交于点F,
则图②中有哪几个等腰三角形?线段EF和EB,FC之间有怎样的关系?
(3)若∠ABC≠∠ACB,其他条件不变,图③中是否还有等腰三角形?
(2)中第二问的关系是否还存在?写出你的理由.
知识点整合训练
(3)等腰三角形有△BOE,△COF,仍有EF=EB+FC.理由:∵BO,CO分别平分∠ABC,∠ACB,∴∠EBO=∠OBC,∠FCO=∠OCB.又∵EF∥BC,∴∠OBC=∠BOE,∠OCB=∠COF,∴∠BOE=∠EBO,∠COF=∠FCO,∴EB=EO,FC=FO.∴EF=EO+FO=EB+FC
谢 谢!
第一章 三角形的证明
1.1 等腰三角形
第3课时 等腰三角形的判定与反证法
核心提要
B
D
核心提要
3.(3分)在方格纸上有一个△ABC,它的顶点位置如图所示,
则这个三角形是____三角形.
4.(3分)聪明的亮亮用含有30°角的两个完全相同的三角板拼成
如图所示的图案,并发现图中有等腰三角形,
请你帮他找出两个等腰三角形:
_________________________.
等腰
△ABE,△DCE,△BCE
核心提要
5.(7分)如图,将长方形ABCD沿对角线BD翻折,点C落在点E的位置,
BE交AD于点F.
求证:重叠部分(即△BDF)是等腰三角形.
证明:∵四边形ABCD是长方形,∴AD∥BC,∴∠ADB=∠DBC.
又∵△BDE与△BDC关于BD所在的直线对称,∴∠FBD=∠DBC,
∴∠BDE与∠BDC关于BD所在的直线对称,
∴∠FBD=∠DBC.∴∠ADB=∠FBD,∴DF=BF,
∴重叠部分(即△BDF)是等腰三角形
核心提要
6.(7分)(内江中考)如图,AD平分∠BAC,AD⊥BD,垂足为点D,
DE∥AC.
求证:△BDE是等腰三角形.
证明:如图,∵DE∥AC,∴∠1=∠3,∵AD平分∠BAC,
∴∠1=∠2,∴∠2=∠3,∵AD⊥BD,∴∠2+∠B=90°,
∠3+∠BDE=90°,∴∠B=∠BDE,∴△BDE是等腰三角形
核心提要
C
核心提要
8.(3分)(驻马店月考)在用反证法证明命题“在一个三角形中,
至少有一个内角大于或等于60°”时,
应首先假设__________________________________.
在一个三角形中,三个内角都小于60°
核心提要
9.(8分)用反证法证明:等腰三角形的两底角必为锐角.
证明:①假设等腰三角形的底角∠B,∠C都是直角,
则_____________________,
从而____________________>180°,
这与___________________矛盾.
②设等腰三角形的底角∠B,∠C都是钝角,
则_________________,从而_________________________,
这与___________________矛盾.
综上所述,假设①,②_______________,
所以∠B,∠C只能为____.
故等腰三角形的两底角必为锐角.
∠B=∠C=90°
∠A+∠B+∠C
三角形内角和为180°
∠B+∠C>180°
∠A+∠B+∠C>180°
三角形内角和为180°
均不成立
锐角
知识点整合训练
D
知识点整合训练
11.如图所示,在△ABC中,∠ABC与∠ACB的平分线交于点O.
过O点作DE∥BC,分别交AB,AC于点D,E.若AB=5,AC=4,
则△ADE的周长是____.
12.在一次夏令营活动中,小明同学从营地A出发,
要到A地的北偏东60°方向的C处.
他先沿正东方向走了200 m到达B地,再沿北偏东30°方向走,
恰能到达目的地C,如图所示,由此可知,B,C两地相距____m.
9
200
知识点整合训练
13.(12分)如图,在△ABC中,D,E分别是AC,AB上的点,
BD与CE交于点O.给出下列四个条件:
①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.
上述四个条件中,哪两个条件可判定△ABC是等腰三角形?
选择其中的一种情形,证明△ABC是等腰三角形.
知识点整合训练
知识点整合训练
14.(12分)如图所示,在四边形ABDC中,AB=AC,∠B=∠C,
求证:BD=CD.
证明:连接BC,∵AB=AC,∴∠ABC=∠ACB.
∵∠ABD=∠ACD,∴∠ABD-∠ABC=∠ACD-∠ACB,
即∠DBC=∠DCB,∴BD=CD
知识点整合训练
【综合运用】
15.(18分)如图所示,在△ABC中,已知∠ABC=∠ACB,
BO平分∠ABC,CO平分∠ACB.
(1)想想看,你能得到什么结论?
(2)若过点O作一直线EF和边BC平行,与AB交于点E,与AC交于点F,
则图②中有哪几个等腰三角形?线段EF和EB,FC之间有怎样的关系?
(3)若∠ABC≠∠ACB,其他条件不变,图③中是否还有等腰三角形?
(2)中第二问的关系是否还存在?写出你的理由.
知识点整合训练
(3)等腰三角形有△BOE,△COF,仍有EF=EB+FC.理由:∵BO,CO分别平分∠ABC,∠ACB,∴∠EBO=∠OBC,∠FCO=∠OCB.又∵EF∥BC,∴∠OBC=∠BOE,∠OCB=∠COF,∴∠BOE=∠EBO,∠COF=∠FCO,∴EB=EO,FC=FO.∴EF=EO+FO=EB+FC
谢 谢!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
