5.3平行线的性质(2)
文档属性
| 名称 | 5.3平行线的性质(2) |

|
|
| 格式 | zip | ||
| 文件大小 | 324.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-18 00:00:00 | ||
图片预览

文档简介
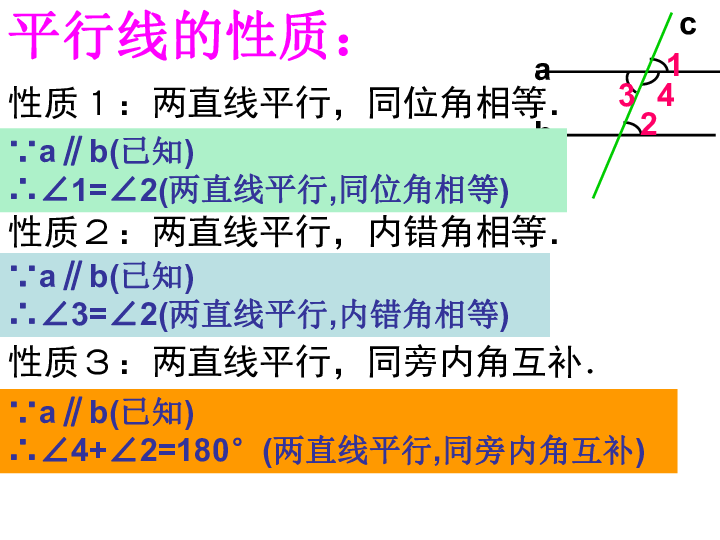
课件15张PPT。5 .3 平行线的性质(2)性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
平行线的性质:∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)∵a∥b(已知)
∴∠3=∠2(两直线平行,内错角相等)∵a∥b(已知)
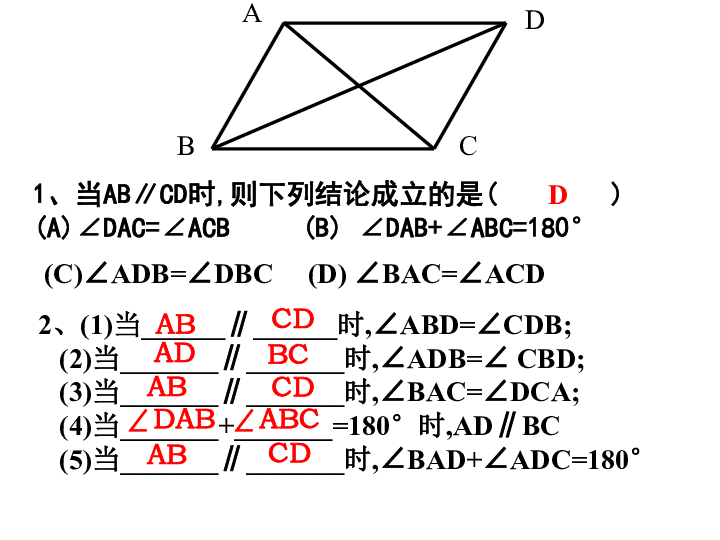
∴∠4+∠2=180°(两直线平行,同旁内角互补)ABCD2、(1)当______∥______时,∠ABD=∠CDB;
(2)当_______∥_______时,∠ADB=∠ CBD;
(3)当_______∥_______时,∠BAC=∠DCA;
(4)当_______+_______=180°时,AD∥BC
(5)当_______∥_______时,∠BAD+∠ADC=180°1、当AB∥CD时,则下列结论成立的是( )
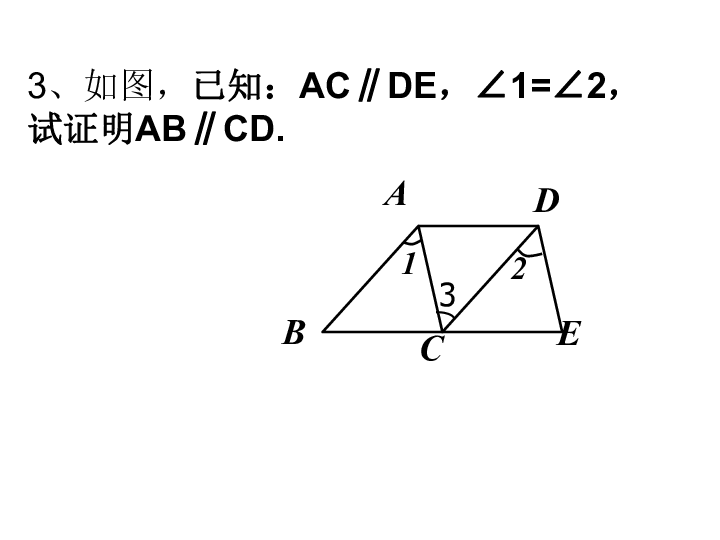
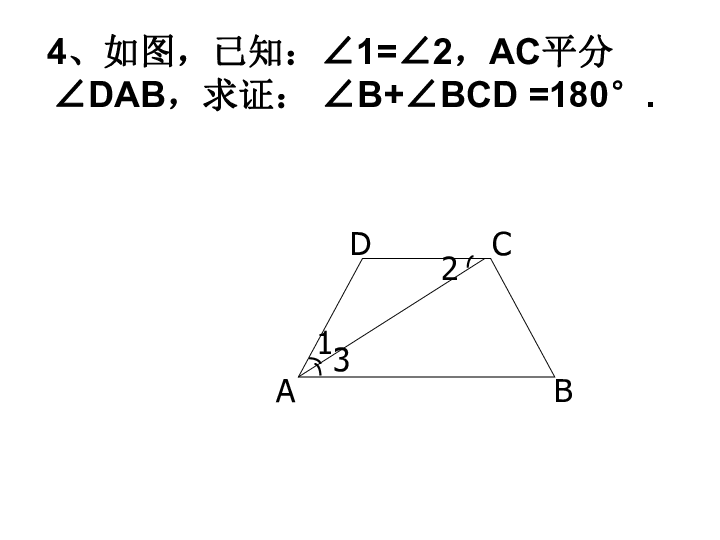
∠DAC=∠ACB (B) ∠DAB+∠ABC=180°(C)∠ADB=∠DBC (D) ∠BAC=∠ACD DABCDADBCABCD∠DAB∠ABCABCD3、如图,已知:AC∥DE,∠1=∠2, 试证明AB∥CD. 4、如图,已知:∠1=∠2,AC平分∠DAB,求证: ∠B+∠BCD =180°.5、如图,已知:AB∥CD,∠A= ∠ C,
求证:AD∥BC。∵∠1=∠2∴AB//CD∴∠3=∠A∵∠A=∠C∴∠3=∠C∴AE∥BC解:(已知)(同位角相等,两直线平行)(两直线平行,同位角相等)(已知)(等量代换)(内错角相等,两直线平行)6、已知:如图∠1=∠2, ∠A=∠C, 说明:AE∥BC7、如图,若AB∥CD,DA平分 ∠ BDC, DE⊥BD,∠ B=108°求∠ A和∠ADE的度数. 8、如图,EF⊥AB,CD⊥AB,∠EFB=∠GDC,
求证:∠AGD=∠ACB。12⌒⌒ABCDE60°32°12F解:过E作EF//AB∵AB//CD∴EF//CD∴∠1=∠B=60°∴∠2=∠D=32°∴∠BED=∠1+ ∠2 =60°+ 32°= 92°9、 已知:如图AB∥CD, ∠ABE= 60°, ∠CDE= 32°,求∠BED的度数.变式⌒⌒ABDE120°110°12F已知:如图AB∥CD, ∠ABE= 120°, ∠CDE= 110°,求∠BED的度数.C10、如图:∠BED=∠B+∠D,
求证:AB∥CDA1A2A3A4A5A6B1B2B3B4B5C1C2C3C4C5像这样,同时垂直于两条平行线并且夹在
这两条平行线间的线段的长度,叫做这两
条平行线的距离.11、用三角尺和直尺画平行线,做成一张5×5个格子的方格纸.观察做出的方格纸的一部分,线段B1C1,B2C2,…,B5C5都与两条平行的横线A1B5和A2C5垂直吗?它们的长度相等吗?CDEABF两点间的距离:连接两点
的线段的长度. 点到直线的距离:直线外
一点到这条直线的垂线段
的长度.两平行线的距离:夹在两平行线间的垂线段的长度.如图,如果AB∥CD,在CD上任取一点E,向AB作垂线段EF,这时,EF是否也垂直于直线CD呢?我们这样作出的垂线段EF的长度d是平行线AB、CD的距离吗? 知识回顾1、直线的位置关系哪有几种?2、怎样判定两直线平行?3、平行公理a ∥b,b∥c c∥a,经过直线外一点,有且只有一条直线和这条直线平行平行相交垂直斜交4. 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行.再见!
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
平行线的性质:∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)∵a∥b(已知)
∴∠3=∠2(两直线平行,内错角相等)∵a∥b(已知)
∴∠4+∠2=180°(两直线平行,同旁内角互补)ABCD2、(1)当______∥______时,∠ABD=∠CDB;
(2)当_______∥_______时,∠ADB=∠ CBD;
(3)当_______∥_______时,∠BAC=∠DCA;
(4)当_______+_______=180°时,AD∥BC
(5)当_______∥_______时,∠BAD+∠ADC=180°1、当AB∥CD时,则下列结论成立的是( )
∠DAC=∠ACB (B) ∠DAB+∠ABC=180°(C)∠ADB=∠DBC (D) ∠BAC=∠ACD DABCDADBCABCD∠DAB∠ABCABCD3、如图,已知:AC∥DE,∠1=∠2, 试证明AB∥CD. 4、如图,已知:∠1=∠2,AC平分∠DAB,求证: ∠B+∠BCD =180°.5、如图,已知:AB∥CD,∠A= ∠ C,
求证:AD∥BC。∵∠1=∠2∴AB//CD∴∠3=∠A∵∠A=∠C∴∠3=∠C∴AE∥BC解:(已知)(同位角相等,两直线平行)(两直线平行,同位角相等)(已知)(等量代换)(内错角相等,两直线平行)6、已知:如图∠1=∠2, ∠A=∠C, 说明:AE∥BC7、如图,若AB∥CD,DA平分 ∠ BDC, DE⊥BD,∠ B=108°求∠ A和∠ADE的度数. 8、如图,EF⊥AB,CD⊥AB,∠EFB=∠GDC,
求证:∠AGD=∠ACB。12⌒⌒ABCDE60°32°12F解:过E作EF//AB∵AB//CD∴EF//CD∴∠1=∠B=60°∴∠2=∠D=32°∴∠BED=∠1+ ∠2 =60°+ 32°= 92°9、 已知:如图AB∥CD, ∠ABE= 60°, ∠CDE= 32°,求∠BED的度数.变式⌒⌒ABDE120°110°12F已知:如图AB∥CD, ∠ABE= 120°, ∠CDE= 110°,求∠BED的度数.C10、如图:∠BED=∠B+∠D,
求证:AB∥CDA1A2A3A4A5A6B1B2B3B4B5C1C2C3C4C5像这样,同时垂直于两条平行线并且夹在
这两条平行线间的线段的长度,叫做这两
条平行线的距离.11、用三角尺和直尺画平行线,做成一张5×5个格子的方格纸.观察做出的方格纸的一部分,线段B1C1,B2C2,…,B5C5都与两条平行的横线A1B5和A2C5垂直吗?它们的长度相等吗?CDEABF两点间的距离:连接两点
的线段的长度. 点到直线的距离:直线外
一点到这条直线的垂线段
的长度.两平行线的距离:夹在两平行线间的垂线段的长度.如图,如果AB∥CD,在CD上任取一点E,向AB作垂线段EF,这时,EF是否也垂直于直线CD呢?我们这样作出的垂线段EF的长度d是平行线AB、CD的距离吗? 知识回顾1、直线的位置关系哪有几种?2、怎样判定两直线平行?3、平行公理a ∥b,b∥c c∥a,经过直线外一点,有且只有一条直线和这条直线平行平行相交垂直斜交4. 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行.再见!
