5.2.2平行线的判定
图片预览




文档简介
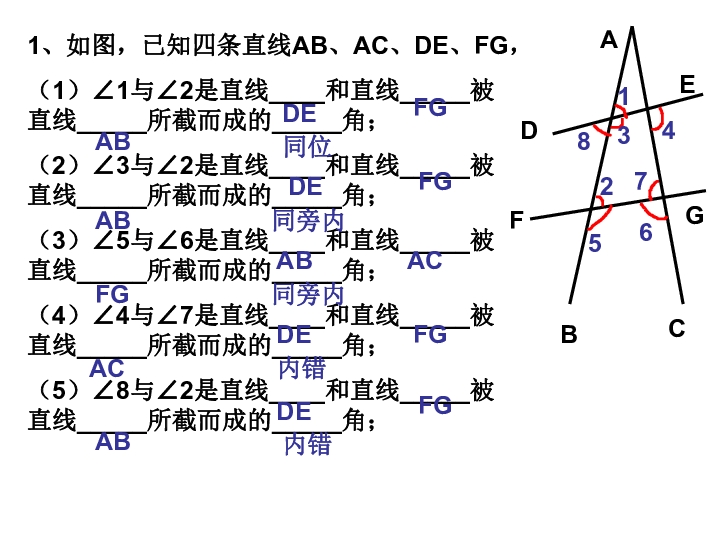
课件26张PPT。5.2.2 平行线的判定(1) 根据定义. (2) 根据平行公理的推论.1.梳理旧知,引出新课 如何判断两条直线是否平行? 同一平面内,存在一条直线a与直线b不相交的位置,这时直线a与b互相平行.平行公理推论:如果两条直线都与第三条直线平行,那么这条直线也互相平行.1、如图,已知四条直线AB、AC、DE、FG,
(1)∠1与∠2是直线____和直线_____被直线_____所截而成的_____角;
(2)∠3与∠2是直线____和直线_____被直线_____所截而成的_____角;
(3)∠5与∠6是直线____和直线_____被直线_____所截而成的_____角;
(4)∠4与∠7是直线____和直线_____被直线_____所截而成的_____角;
(5)∠8与∠2是直线____和直线_____被直线_____所截而成的_____角;GDEFG同位ABDEFGAB同旁内ABACFG同旁内DEFGAC内错DEFGAB内错2、如果a//b,b//c,那么____________,
理由是a//c如果两条直线都与第三条直线平行,那么这条直线也互相平行2、平行线的画法:2. 动手操作,归纳方法 你还记得如何用直尺和三角尺画平行线吗?2、平行线的画法:·ABCD2.动手操作,归纳方法 你还记得如何用直尺和三角尺画平行线吗?画平行线方法:
一“落”:三角板的一边落在已知直线上;
二“靠”:用直尺紧靠三角板的另一边;
三“移”:沿直尺移动三角板,直至落在已知直线上的三角板的一边经过已知点;
四“画”:沿三角板过已知点的边画直线。如图,在用直尺和三角板画平行线的过程中,三角板起着什么样的作用?结果:三角板的作用是使∠ECD与∠EAB相等。E这两个角有什么位置关系?大家能否
总结出一
个平行的
判定呢?同位角判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单记为:同位角相等,两条直线平行。用符号语言如何表达两条直线平行?如果∠1=∠2,那么AB//CD问题:木工用角尺画平行线的过程中,试说出用角尺画平行线的道理。
讨论结果:如图,因为∠DCB与∠FEB是直线CD、EF被AB所截而成的同位角,而且∠DCB=∠FEB,即同位角相等,根据直线平行判定1,从而CD//EF如果∠1=∠2,那么AB//CD,为什么?如何证明?提示:转化为同位角判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单记为:内错角相等,两条直线平行。用符号语言如何表示?同旁内角要满足什么关系时,两直线才平行?相等判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单记为:同旁内角互补,两条直线平行。如何证明?提示:转化成已学的角 判定方法1 同位角相等,两直线平行. 判定方法2 内错角相等,两直线平行.判定方法3 同旁内角互补,两直线平行. 平行线的判定(1)由∠CBE=∠A可以判定哪两条直线平行?
根据是什么?4.巩固新知,深化理解答: AD∥BC .根据同位角相等,两直线平行.(2)由∠CBE=∠C可以判定哪两条直线平行?
根据是什么?4.巩固新知,深化理解例2 如图, BE是AB的延长线.答: AE∥CD .根据内错角相等,两直线平行.(3)由∠D+∠A= 180°可以判定哪两条直线平
行?根据是什么?4.巩固新知,深化理解例2 如图, BE是AB的延长线.答: AE∥CD .根据同旁内角互补,两直线平行.例题:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
判断题:
1、两条直线被第三条直线所截,如果同位角相等,那么内错角也相等。
2、两条直线被第三条直线所截,如果内错角互补,那么同旁内角相等。根据定义. 根据平行公理的推论.1.梳理旧知,归纳方法 问题1 (1)判定两条直线平行的方法有哪些? 判定方法1 同位角相等,两直线平行. 判定方法2 内错角相等,两直线平行.判定方法3 同旁内角互补,两直线平行.(2)结合图形回答问题:答: AB∥CD .根据内错角相等,两直线平行.1.梳理旧知,归纳方法①如果∠1=∠2,能判定哪两条直线平行?为什么?(2)结合图形回答问题:答: DE∥FB.根据同位角相等,两直线平行.1.梳理旧知,归纳方法②如果∠1=∠3,能判定哪两条直线平行?为什么?(2)结合图形回答问题:答: AD∥CB.根据同旁内角互补,两直线平行.1.梳理旧知,归纳方法③如果∠A+∠ ABC=180o ,能判定哪两条直线平行?为什么?2.学会分析,应用方法问题2 如图,当∠1=∠2时,AB 与CD平行吗?
为什么?答: AB∥CD .
理由如下:
∵ ∠1=∠2,
又∵ ∠2=∠3 ,
∴ ∠1=∠3 .
∵ ∠1和∠3是同位角 ,
∴ AB∥CD(同位角相等,两直线平行).2.学会分析,应用方法已知条件:直线b与直线c都垂直于直线a.
要说明的结论:直线b与直线c平行吗?问题3 在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?2.学会分析,应用方法已知:直线b与直线c都垂直于直线a.
说明:直线b与直线c平行吗?答:直线b与直线c平行.理由如下:
∵ b⊥a,∴ ∠1= 90°.
同理∠2= 90°.
∴ ∠1=∠2.
∵ ∠1和∠2是同位角,
∴ b∥c(同位角相等,两直线平行).12你还能用其他方法说明理由吗?3.应用迁移,深化理解答: AB∥CD .
理由如下:
∵ AC平分∠BAD,
∴ ∠1=∠3 .
∵∠1=∠2,
∴ ∠2=∠3 .
∵ ∠2和∠3是内错角,
∴ AB∥CD(内错角相等,两直线平行).问题4 已知:如图,四边形ABCD中,AC平分∠BAD,∠1=∠2,AB与CD平行吗?为什么?作业:
(1)∠1与∠2是直线____和直线_____被直线_____所截而成的_____角;
(2)∠3与∠2是直线____和直线_____被直线_____所截而成的_____角;
(3)∠5与∠6是直线____和直线_____被直线_____所截而成的_____角;
(4)∠4与∠7是直线____和直线_____被直线_____所截而成的_____角;
(5)∠8与∠2是直线____和直线_____被直线_____所截而成的_____角;GDEFG同位ABDEFGAB同旁内ABACFG同旁内DEFGAC内错DEFGAB内错2、如果a//b,b//c,那么____________,
理由是a//c如果两条直线都与第三条直线平行,那么这条直线也互相平行2、平行线的画法:2. 动手操作,归纳方法 你还记得如何用直尺和三角尺画平行线吗?2、平行线的画法:·ABCD2.动手操作,归纳方法 你还记得如何用直尺和三角尺画平行线吗?画平行线方法:
一“落”:三角板的一边落在已知直线上;
二“靠”:用直尺紧靠三角板的另一边;
三“移”:沿直尺移动三角板,直至落在已知直线上的三角板的一边经过已知点;
四“画”:沿三角板过已知点的边画直线。如图,在用直尺和三角板画平行线的过程中,三角板起着什么样的作用?结果:三角板的作用是使∠ECD与∠EAB相等。E这两个角有什么位置关系?大家能否
总结出一
个平行的
判定呢?同位角判定方法1 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单记为:同位角相等,两条直线平行。用符号语言如何表达两条直线平行?如果∠1=∠2,那么AB//CD问题:木工用角尺画平行线的过程中,试说出用角尺画平行线的道理。
讨论结果:如图,因为∠DCB与∠FEB是直线CD、EF被AB所截而成的同位角,而且∠DCB=∠FEB,即同位角相等,根据直线平行判定1,从而CD//EF如果∠1=∠2,那么AB//CD,为什么?如何证明?提示:转化为同位角判定方法2 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单记为:内错角相等,两条直线平行。用符号语言如何表示?同旁内角要满足什么关系时,两直线才平行?相等判定方法3 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单记为:同旁内角互补,两条直线平行。如何证明?提示:转化成已学的角 判定方法1 同位角相等,两直线平行. 判定方法2 内错角相等,两直线平行.判定方法3 同旁内角互补,两直线平行. 平行线的判定(1)由∠CBE=∠A可以判定哪两条直线平行?
根据是什么?4.巩固新知,深化理解答: AD∥BC .根据同位角相等,两直线平行.(2)由∠CBE=∠C可以判定哪两条直线平行?
根据是什么?4.巩固新知,深化理解例2 如图, BE是AB的延长线.答: AE∥CD .根据内错角相等,两直线平行.(3)由∠D+∠A= 180°可以判定哪两条直线平
行?根据是什么?4.巩固新知,深化理解例2 如图, BE是AB的延长线.答: AE∥CD .根据同旁内角互补,两直线平行.例题:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
判断题:
1、两条直线被第三条直线所截,如果同位角相等,那么内错角也相等。
2、两条直线被第三条直线所截,如果内错角互补,那么同旁内角相等。根据定义. 根据平行公理的推论.1.梳理旧知,归纳方法 问题1 (1)判定两条直线平行的方法有哪些? 判定方法1 同位角相等,两直线平行. 判定方法2 内错角相等,两直线平行.判定方法3 同旁内角互补,两直线平行.(2)结合图形回答问题:答: AB∥CD .根据内错角相等,两直线平行.1.梳理旧知,归纳方法①如果∠1=∠2,能判定哪两条直线平行?为什么?(2)结合图形回答问题:答: DE∥FB.根据同位角相等,两直线平行.1.梳理旧知,归纳方法②如果∠1=∠3,能判定哪两条直线平行?为什么?(2)结合图形回答问题:答: AD∥CB.根据同旁内角互补,两直线平行.1.梳理旧知,归纳方法③如果∠A+∠ ABC=180o ,能判定哪两条直线平行?为什么?2.学会分析,应用方法问题2 如图,当∠1=∠2时,AB 与CD平行吗?
为什么?答: AB∥CD .
理由如下:
∵ ∠1=∠2,
又∵ ∠2=∠3 ,
∴ ∠1=∠3 .
∵ ∠1和∠3是同位角 ,
∴ AB∥CD(同位角相等,两直线平行).2.学会分析,应用方法已知条件:直线b与直线c都垂直于直线a.
要说明的结论:直线b与直线c平行吗?问题3 在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?2.学会分析,应用方法已知:直线b与直线c都垂直于直线a.
说明:直线b与直线c平行吗?答:直线b与直线c平行.理由如下:
∵ b⊥a,∴ ∠1= 90°.
同理∠2= 90°.
∴ ∠1=∠2.
∵ ∠1和∠2是同位角,
∴ b∥c(同位角相等,两直线平行).12你还能用其他方法说明理由吗?3.应用迁移,深化理解答: AB∥CD .
理由如下:
∵ AC平分∠BAD,
∴ ∠1=∠3 .
∵∠1=∠2,
∴ ∠2=∠3 .
∵ ∠2和∠3是内错角,
∴ AB∥CD(内错角相等,两直线平行).问题4 已知:如图,四边形ABCD中,AC平分∠BAD,∠1=∠2,AB与CD平行吗?为什么?作业:
