4-3-5三角形全等综合课七年级数学下学期同步探讲练课件(北师大版)
文档属性
| 名称 | 4-3-5三角形全等综合课七年级数学下学期同步探讲练课件(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 00:00:00 | ||
图片预览


文档简介
(共13张PPT)
北师※七(下)
4.3 探索三角形全等的条件
第六课时
对应相等的元素 两边一角 两角一边 三角 三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边
三角形是否全等
一定
(SAS)
不一定
一定
(ASA)
一定
(AAS)
一定
(SSS)
不一定
判定三角形全等时最少有几组边对应相等 最多有几组边
判定三角形全等时最少有几组角对应相等 最多有几组角
知识回顾
最少1条边
最少一个角
最多两个角
最多3条边
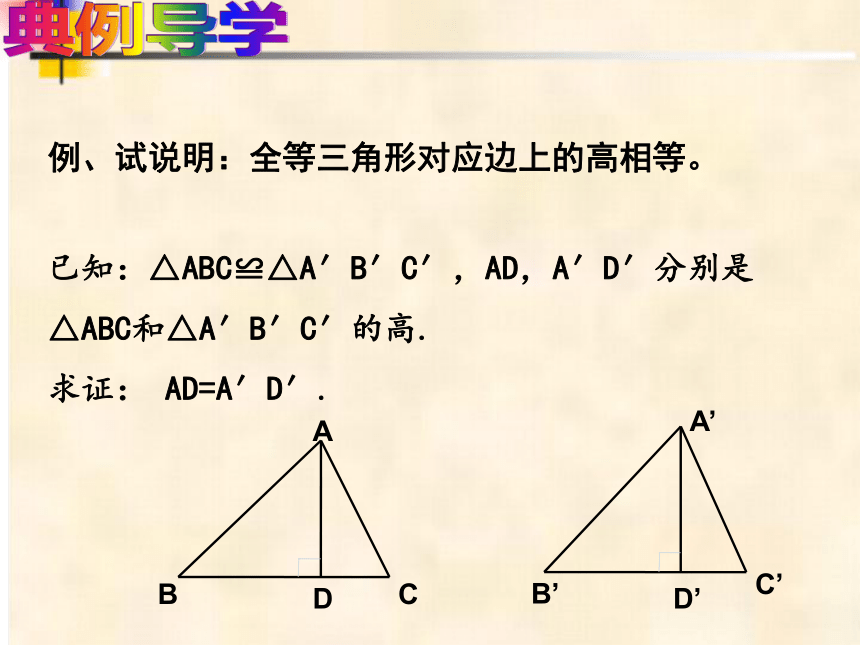
已知:△ABC≌△A′B′C′,AD,A′D′分别是△ABC和△A′B′C′的高.
求证: AD=A′D′.
A
B
D
C
B’
A’
C’
D’
典例导学
例、试说明:全等三角形对应边上的高相等。
典例导学
A
B
D
C
B’
A’
C’
D’
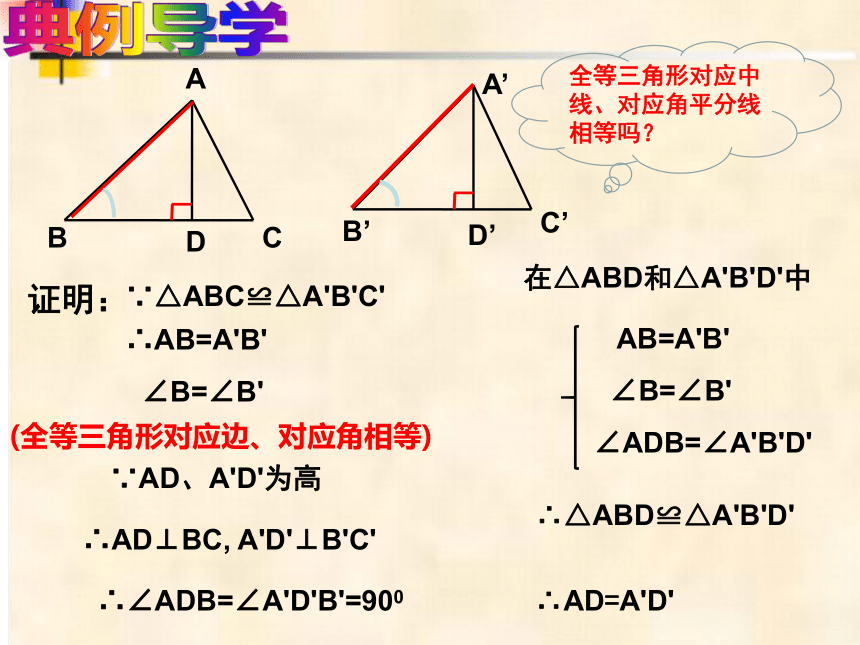
证明:
∵△ABC≌△A'B'C'
∴AB=A'B'
∠B=∠B'
(全等三角形对应边、对应角相等)
∵AD、A'D'为高
∴AD⊥BC, A'D'⊥B'C'
∴∠ADB=∠A'D'B'=900
在△ABD和△A'B'D'中
AB=A'B'
∠B=∠B'
∠ADB=∠A'B'D'
∴△ABD≌△A'B'D'
∴AD=A'D'
全等三角形对应中线、对应角平分线相等吗?
夯实基础
(ASA)
(SSS)
不一定全等
(ASA)
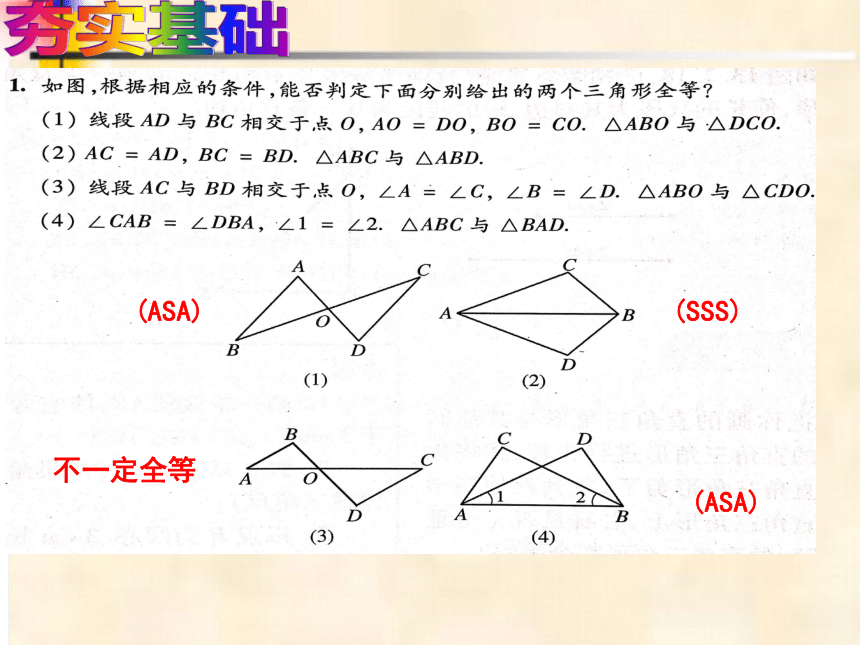
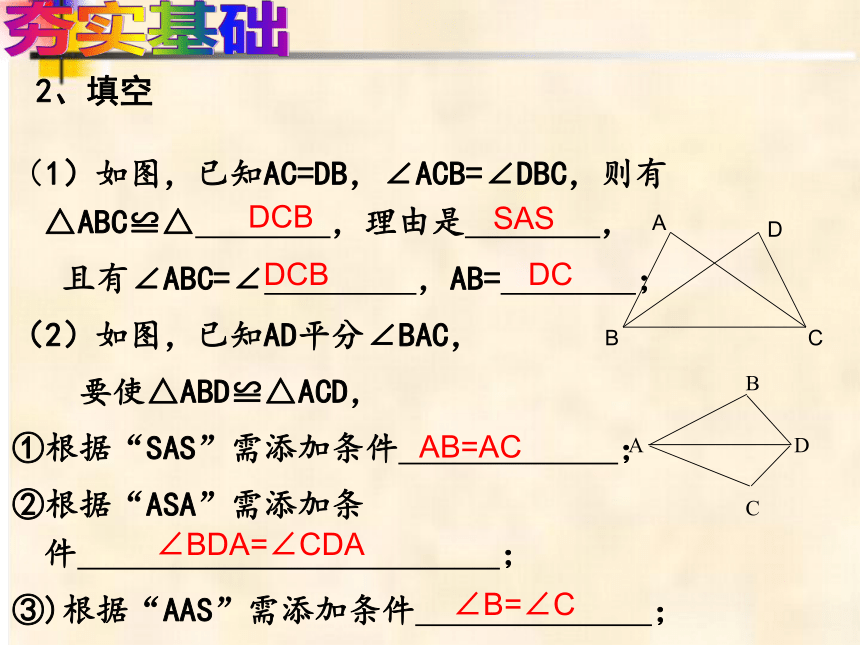
(1)如图,已知AC=DB,∠ACB=∠DBC,则有△ABC≌△ ,理由是 ,
且有∠ABC=∠ ,AB= ;
(2)如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
①根据“SAS”需添加条件 ;
②根据“ASA”需添加条件 ;
③)根据“AAS”需添加条件 ;
A
B
C
D
A
B
C
D
DCB
SAS
DCB
DC
AB=AC
∠BDA=∠CDA
∠B=∠C
夯实基础
2、填空
(3)如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上。
①AC∥BD,CF=DE, (SAS)
② AC=BD, AC∥BD (ASA)
③ CE=DF, (ASA)
④∠ C= ∠D,CE=DF ,AE BF (ASA)
C
B
A
E
F
D
∠AEC=∠BFD
AC=BD
∠A=∠B
∠C=∠D
∥
夯实基础
3.如图,∠1=∠2,∠3=∠4,则图中全等三角形的对数是( )
A. 3 B. 4
C. 5 D. 6
夯实基础
△ABD≌△CBD
(ASA)
△ABE≌△CBE
(SAS)
△ADF≌△CDF
(SAS)
△AEF≌△CEF
(SSS)
△ABF≌△CBF
(SAS)
△ADE≌△CCD
(SAS)
能力提升
1、如图,AE=AD,AB=AC
求证:BO=CO
要证:△ABE≌△ACD
要得:BO=CO
思路导航
需证:△BOD≌△COE
(已有一角对应相等)
要证:BD=CE
∠B=∠C
请你写出具体的证明过程!
由AB=AC,AE=AD可得
能力提升
1、如图,AE=AD,AB=AC
求证:BO=CO
证明:在△ABE和ACD中
∠BAE=∠CAD
AB=AC
AE=AD
∴ △ABE ≌ △ACD
(SAS)
(公共角)
∵AB=AC,AD=AE
∴BD=CE
∠B=∠C
BD=CE
∴ △BDO ≌ △CEO
∴BO=CO
∠B0D=∠COE
(等式的性质)
(对顶角相等)
(AAS)
∴∠B=∠C
能力提升
2、如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O。求证:EC=ED
要得:EC=ED
思路导航
需证:△BED≌△AEC
(已有一角一边对应相等)
要证:∠BED=∠AEC
请你写出具体的证明过程!
要证:∠BEA=∠2
(利用∠BEA转化)
能力提升
2、如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O。求证:EC=ED
证明:
∵∠A=∠B
∠AOD=∠BOE
∴∠BEO=∠2
∵∠1=∠2
∴∠1=∠BEO
∴∠1+∠AEO=∠BEO+∠AEO
即:∠BED=∠AEC
(等式性质)
(等量代换)
BE=AE
∠BED=∠AEC
∠A=∠B
∴ △BED ≌ △AEC
∴ED=EC
在△BED和△AEC中
(ASA)
对应相等的元素 两边一角 两角一边 三角 三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边
三角形是否全等
一定
(SAS)
不一定
一定
(ASA)
一定
(AAS)
一定
(SSS)
不一定
判定三角形全等时最少有几组边对应相等 最多有几组边
判定三角形全等时最少有几组角对应相等 最多有几组角
课堂小结
最少1条边
最少一个角
最多两个角
最多3条边
北师※七(下)
4.3 探索三角形全等的条件
第六课时
对应相等的元素 两边一角 两角一边 三角 三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边
三角形是否全等
一定
(SAS)
不一定
一定
(ASA)
一定
(AAS)
一定
(SSS)
不一定
判定三角形全等时最少有几组边对应相等 最多有几组边
判定三角形全等时最少有几组角对应相等 最多有几组角
知识回顾
最少1条边
最少一个角
最多两个角
最多3条边
已知:△ABC≌△A′B′C′,AD,A′D′分别是△ABC和△A′B′C′的高.
求证: AD=A′D′.
A
B
D
C
B’
A’
C’
D’
典例导学
例、试说明:全等三角形对应边上的高相等。
典例导学
A
B
D
C
B’
A’
C’
D’
证明:
∵△ABC≌△A'B'C'
∴AB=A'B'
∠B=∠B'
(全等三角形对应边、对应角相等)
∵AD、A'D'为高
∴AD⊥BC, A'D'⊥B'C'
∴∠ADB=∠A'D'B'=900
在△ABD和△A'B'D'中
AB=A'B'
∠B=∠B'
∠ADB=∠A'B'D'
∴△ABD≌△A'B'D'
∴AD=A'D'
全等三角形对应中线、对应角平分线相等吗?
夯实基础
(ASA)
(SSS)
不一定全等
(ASA)
(1)如图,已知AC=DB,∠ACB=∠DBC,则有△ABC≌△ ,理由是 ,
且有∠ABC=∠ ,AB= ;
(2)如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
①根据“SAS”需添加条件 ;
②根据“ASA”需添加条件 ;
③)根据“AAS”需添加条件 ;
A
B
C
D
A
B
C
D
DCB
SAS
DCB
DC
AB=AC
∠BDA=∠CDA
∠B=∠C
夯实基础
2、填空
(3)如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上。
①AC∥BD,CF=DE, (SAS)
② AC=BD, AC∥BD (ASA)
③ CE=DF, (ASA)
④∠ C= ∠D,CE=DF ,AE BF (ASA)
C
B
A
E
F
D
∠AEC=∠BFD
AC=BD
∠A=∠B
∠C=∠D
∥
夯实基础
3.如图,∠1=∠2,∠3=∠4,则图中全等三角形的对数是( )
A. 3 B. 4
C. 5 D. 6
夯实基础
△ABD≌△CBD
(ASA)
△ABE≌△CBE
(SAS)
△ADF≌△CDF
(SAS)
△AEF≌△CEF
(SSS)
△ABF≌△CBF
(SAS)
△ADE≌△CCD
(SAS)
能力提升
1、如图,AE=AD,AB=AC
求证:BO=CO
要证:△ABE≌△ACD
要得:BO=CO
思路导航
需证:△BOD≌△COE
(已有一角对应相等)
要证:BD=CE
∠B=∠C
请你写出具体的证明过程!
由AB=AC,AE=AD可得
能力提升
1、如图,AE=AD,AB=AC
求证:BO=CO
证明:在△ABE和ACD中
∠BAE=∠CAD
AB=AC
AE=AD
∴ △ABE ≌ △ACD
(SAS)
(公共角)
∵AB=AC,AD=AE
∴BD=CE
∠B=∠C
BD=CE
∴ △BDO ≌ △CEO
∴BO=CO
∠B0D=∠COE
(等式的性质)
(对顶角相等)
(AAS)
∴∠B=∠C
能力提升
2、如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O。求证:EC=ED
要得:EC=ED
思路导航
需证:△BED≌△AEC
(已有一角一边对应相等)
要证:∠BED=∠AEC
请你写出具体的证明过程!
要证:∠BEA=∠2
(利用∠BEA转化)
能力提升
2、如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O。求证:EC=ED
证明:
∵∠A=∠B
∠AOD=∠BOE
∴∠BEO=∠2
∵∠1=∠2
∴∠1=∠BEO
∴∠1+∠AEO=∠BEO+∠AEO
即:∠BED=∠AEC
(等式性质)
(等量代换)
BE=AE
∠BED=∠AEC
∠A=∠B
∴ △BED ≌ △AEC
∴ED=EC
在△BED和△AEC中
(ASA)
对应相等的元素 两边一角 两角一边 三角 三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边
三角形是否全等
一定
(SAS)
不一定
一定
(ASA)
一定
(AAS)
一定
(SSS)
不一定
判定三角形全等时最少有几组边对应相等 最多有几组边
判定三角形全等时最少有几组角对应相等 最多有几组角
课堂小结
最少1条边
最少一个角
最多两个角
最多3条边
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
