4-4尺规作三角形七年级数学下学期同步探讲练课件(北师大版)
文档属性
| 名称 | 4-4尺规作三角形七年级数学下学期同步探讲练课件(北师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 00:00:00 | ||
图片预览




文档简介
(共13张PPT)
北师※七(下)
4.4 用尺规作三角形
在几何里,把限定用直尺和圆规来画图,称为尺规作图.其中,直尺是没有刻度的,不能用来度量;圆规用来截取长度或作弧线。
基本概念
我们已会使用刻度尺、三角板、量角器等工具画几何图形,但这种作图存在较大误差。
基本概念
常用的尺规作图,通常称基本作图.一些复杂的尺规图都是由基本作图组成的.
自古希腊时代起,人们就对尺规作图产生极大兴趣。对用尺规作图能作出哪些图形及不能作出哪些图形的思考和研究,推动了整个数学的发展。
下面我们将研究几种基本作图:
已知: ∠AOB。
求作: ∠A`O`B`,使∠A`O`B`= ∠AOB。
1、作一个角等于已知角
做一做
O
A
B
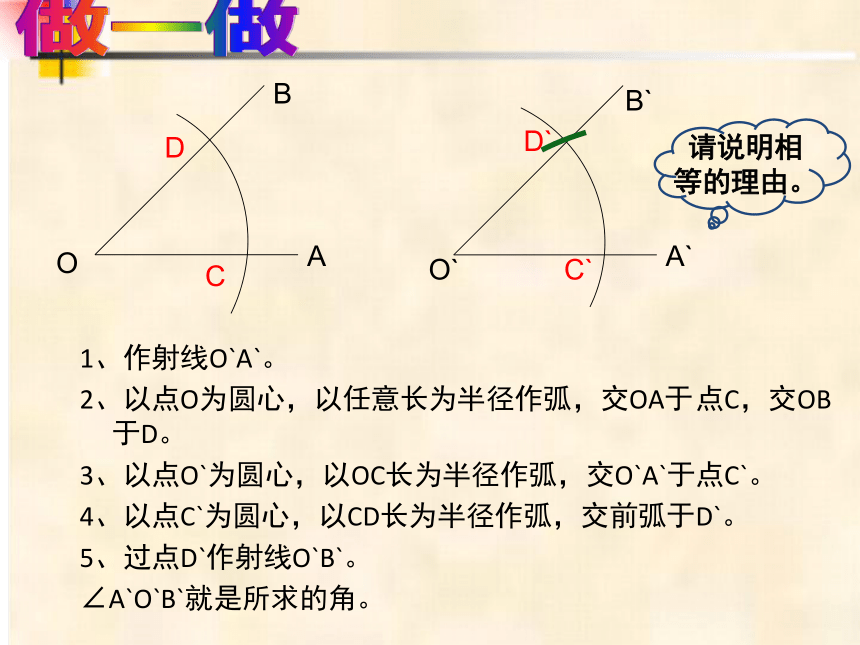
1、作射线O`A`。
2、以点O为圆心,以任意长为半径作弧,交OA于 点C,交OB于D。
3、以点O`为圆心,以OC长为半径作弧,交O`A`于点C`。
4、以点C`为圆心,以CD长为半径作弧,交前弧于D`。
5、过点D`作射线O`B`。
∠A`O`B`就是所求的角。
O
A
B
C
D
O`
A`
C`
D`
B`
请说明相等的理由。
做一做
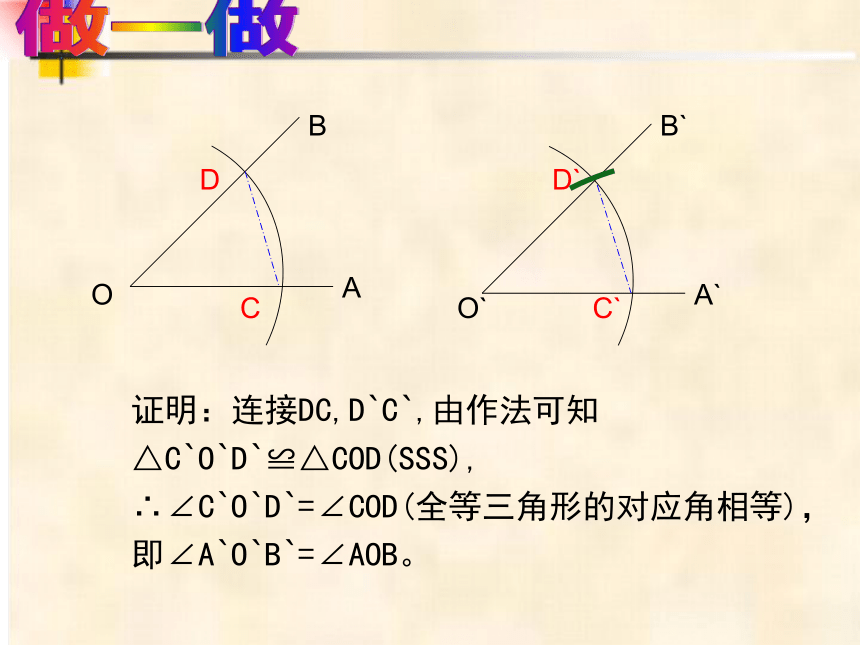
证明:连接DC,D`C`,由作法可知
△C`O`D`≌△COD(SSS),
∴∠C`O`D`=∠COD(全等三角形的对应角相等),
即∠A`O`B`=∠AOB。
O
A
B
C
D
B`
O`
A`
C`
D`
做一做
例、已知:线段a, c, ∠α ,求作:△ABC,使BC=a,AB= c, ∠ABC =∠α.
a
c
α
典例导学
1、已知线段 a,用尺规作△ABC,
使 AB = a,BC = AC = 2a.
夯实基础
请按照给出的作法作出相应的图形.
作法 图形
(1)作 ;
A
F
(2)在射线AF上截取线段AB=c;
C
D
B
A
D
F
A
B
D
F
(3)以B为顶点,以BA为一边,
作 ,BE交AD于点C.
△ABC就是所求作的三角形.
E
2、已知三角形的两角及其夹边,求作这个三角形.
求作:△ABC,使∠A= ,∠B= ,AB=c.
已知: , ,线段c.
c
夯实基础
夯实基础
3.已知∠α和∠β.求作一个角,使它等于∠α-∠β(不写作法,保留作图痕迹)
解:
α
β
A
O
B
C
∠AOC为所求的角
1、已知:线段a, ∠α ,且尺规作一个三角形,使一个内角等于∠α,另一个内角等于2∠α,且这两个角的夹边等于a
a
α
能力提升
2、已知:直线AB及直线AB外一点C;
求作:过点C作CD∥AB。
C
A
B
能力提升
通过本节学习,应理解一些作图语句
过点x、点x作直线;或作直线xx,射线xx.
连结两点x、x;或连结xx;
在xx上截取xx=xx;
以点x为圆心,xx为半径作圆(弧);(交xx于x点;)
分别以点x,点x为圆心,以xx为半径作弧,两弧相交于x点。
课内反思
北师※七(下)
4.4 用尺规作三角形
在几何里,把限定用直尺和圆规来画图,称为尺规作图.其中,直尺是没有刻度的,不能用来度量;圆规用来截取长度或作弧线。
基本概念
我们已会使用刻度尺、三角板、量角器等工具画几何图形,但这种作图存在较大误差。
基本概念
常用的尺规作图,通常称基本作图.一些复杂的尺规图都是由基本作图组成的.
自古希腊时代起,人们就对尺规作图产生极大兴趣。对用尺规作图能作出哪些图形及不能作出哪些图形的思考和研究,推动了整个数学的发展。
下面我们将研究几种基本作图:
已知: ∠AOB。
求作: ∠A`O`B`,使∠A`O`B`= ∠AOB。
1、作一个角等于已知角
做一做
O
A
B
1、作射线O`A`。
2、以点O为圆心,以任意长为半径作弧,交OA于 点C,交OB于D。
3、以点O`为圆心,以OC长为半径作弧,交O`A`于点C`。
4、以点C`为圆心,以CD长为半径作弧,交前弧于D`。
5、过点D`作射线O`B`。
∠A`O`B`就是所求的角。
O
A
B
C
D
O`
A`
C`
D`
B`
请说明相等的理由。
做一做
证明:连接DC,D`C`,由作法可知
△C`O`D`≌△COD(SSS),
∴∠C`O`D`=∠COD(全等三角形的对应角相等),
即∠A`O`B`=∠AOB。
O
A
B
C
D
B`
O`
A`
C`
D`
做一做
例、已知:线段a, c, ∠α ,求作:△ABC,使BC=a,AB= c, ∠ABC =∠α.
a
c
α
典例导学
1、已知线段 a,用尺规作△ABC,
使 AB = a,BC = AC = 2a.
夯实基础
请按照给出的作法作出相应的图形.
作法 图形
(1)作 ;
A
F
(2)在射线AF上截取线段AB=c;
C
D
B
A
D
F
A
B
D
F
(3)以B为顶点,以BA为一边,
作 ,BE交AD于点C.
△ABC就是所求作的三角形.
E
2、已知三角形的两角及其夹边,求作这个三角形.
求作:△ABC,使∠A= ,∠B= ,AB=c.
已知: , ,线段c.
c
夯实基础
夯实基础
3.已知∠α和∠β.求作一个角,使它等于∠α-∠β(不写作法,保留作图痕迹)
解:
α
β
A
O
B
C
∠AOC为所求的角
1、已知:线段a, ∠α ,且尺规作一个三角形,使一个内角等于∠α,另一个内角等于2∠α,且这两个角的夹边等于a
a
α
能力提升
2、已知:直线AB及直线AB外一点C;
求作:过点C作CD∥AB。
C
A
B
能力提升
通过本节学习,应理解一些作图语句
过点x、点x作直线;或作直线xx,射线xx.
连结两点x、x;或连结xx;
在xx上截取xx=xx;
以点x为圆心,xx为半径作圆(弧);(交xx于x点;)
分别以点x,点x为圆心,以xx为半径作弧,两弧相交于x点。
课内反思
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
