5-3-1等腰三角形的性质(第一课时)七年级数学下学期同步探讲练课件(北师大版)
文档属性
| 名称 | 5-3-1等腰三角形的性质(第一课时)七年级数学下学期同步探讲练课件(北师大版) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 09:17:49 | ||
图片预览







文档简介
(共24张PPT)
5.3 简单的轴对称图形
北师版七(下)
等腰三角形的性质
(第一课时)
生活情景
生活情景
生活情景
生活情景
生活情景
以上图片都含有:
等腰三角形
定义:
两条边相等的三角形叫做等腰三角形.
如图AB=AC , 就是等腰三角形
等腰三角形的基本要素:
相等的两边叫做腰
另一边叫做底边
两腰的夹角叫做顶角
腰和底边的夹角叫做底角
A
B
C
腰
腰
底边
顶角
底角
底角
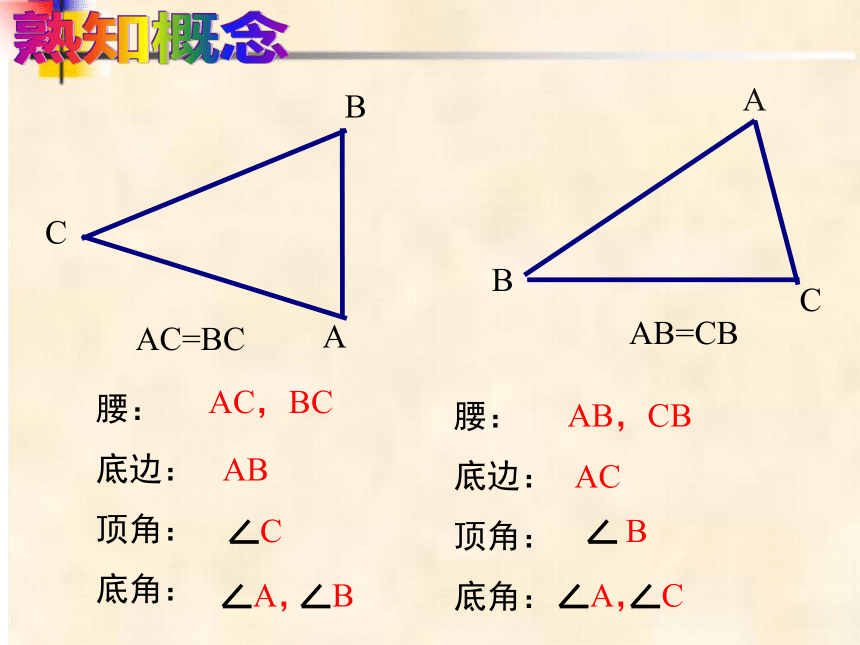
熟知概念
C
A
B
AC=BC
B
C
A
AB=CB
腰:
底边:
顶角:
底角:
腰:
底边:
顶角:
底角:
AC,BC
AB
A,
B
AB,CB
AC
B
A,
C
C
熟知概念
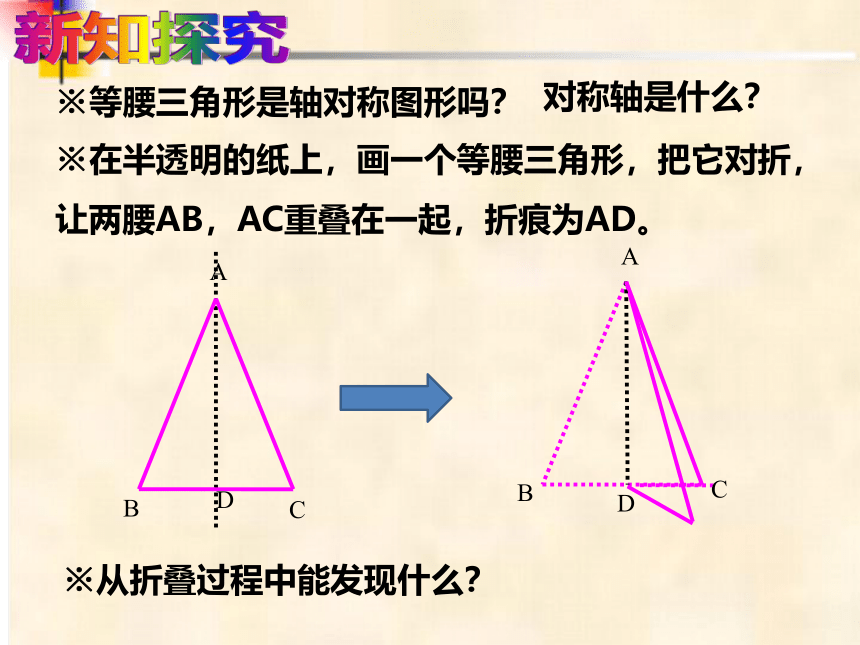
※在半透明的纸上,画一个等腰三角形,把它对折,
让两腰AB,AC重叠在一起,折痕为AD。
新知探究
B
A
C
D
A
B
C
D
※等腰三角形是轴对称图形吗?
对称轴是什么?
※从折叠过程中能发现什么?
重合的线段 重合的角
A
C
B
D
AB=AC
BD=CD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC= 90°
等腰三角形除了两腰相等以外,你还能发现它的其他相等的量吗
新知探究
(AD平分顶角)
(AD为底边的高)
(AD为底边的中线)
对于“∠B=∠C”这一结果如何表述成命题
等腰三角形两底角相等。
C
A
B
D
已知:如图△ABC中,AB=AC.
求证:∠B=∠C.
新知探究
等腰三角形两底角相等。
猜想:
是正确的吗?
定理:
分析:常用什么方法证明线段相等?
如何构造全等三角形?
全等三角形
作AD平分∠BAC
△ABD≌△ACD
(SAS)
∠B=∠C
作BC边中线AD
△ABD≌△ACD
(SSS)
∠B=∠C
新知探究
C
A
B
等腰三角形两底角相等。
定理:
(等边对等角)
在△ABC中,
∵AB=AC
∴∠B=∠C
(等边对等角)
重合的线段 重合的角
A
C
B
D
BD=CD
∠BAD = ∠CAD
∠ADB = ∠ADC= 90°
新知探究
(AD平分顶角)
(AD为底边的高)
(AD为底边的中线)
对于这三个结果如何表述成命题
等腰三角形底边上的中线、高及顶角角平分线互相重合。
已知:如图△ABC中,AB=AC,
求证:BD=CD,
新知探究
猜想:
是真命题吗?
定理:
等腰三角形底边上的中线、高及顶角角平分线互相重合。
AD⊥BC.
AD平分∠BAC
已知:如图△ABC中,AB=AC.
BD=CD.
求证:AD⊥BC,
AD平分∠BAC.
已知:如图△ABC中,AB=AC,
求证:BD=CD,
AD⊥BC
AD平分∠BAC.
(AAS)
(SSS)
C
A
B
D
(SAS)
C
D
B
A
①在ΔABC中,∵AB=AC,
∴ ∠B=∠C( )
等边对等角
(1)∵AB=AC,AD⊥BC,
∴∠____ = ∠____,___= ___
(2)∵AB=AC,AD是中线,
∴___⊥___ , ∠____ =∠____
(3)∵AB=AC,AD是角平分线,
∴___ ⊥___ ,___ =___
BAD CAD
BD CD
AD BC
AD BC
BD CD
②在△ABC中,
知识概括
BAD CAD
(“三线合一”)
(“三线合一”)
(“三线合一”)
例、如图,在△ABC中,AB = AC,D是BC边上的中点,∠BAC = 100°,求 ∠B和 ∠1的度数。
A
B
C
1
2
D
解:
∵∠BAC=1000,
∠B+∠C+∠BAC=1800
∴∠B+∠C=800
∵ AB = AC
∴ ∠B = ∠C =300
∵ AB=AC,D是BC边上的中点
∴∠1= ∠2=500
典例导学
(等式性质)
(等边对等角)
(三线合一)
还有什么不同的方法求∠B?
①等腰三角形一个角为70°,它的另外两个角为
___________________
②等腰三角形一个角为110°,它的另外两个角为________
70°,40°或55°,55°
35°,35°
夯实基础
1、填空
夯实基础
A
B
C
E
D
2、在△ABC中,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D、E。求证:∠DBC=∠ECB
∵AB=AC,
∴∠ABC=∠ACB
∵BD⊥AC,CE⊥AB
∴ ∠BDC=∠CEB=900
在△BEC和△CDB中
∠ABC=∠ACB
∠BDC=∠CEB
BC=CB
∴△ABD≌△ACD
∴∠DBC=∠EBC
证明:
(等边对等角)
(公共边)
还有其他解法吗?
夯实基础
A
B
C
E
D
2、在△ABC中,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D、E。求证:∠DBC=∠ECB
证明:
AB=AC
△ABD≌△ACE
(AAS)
∠ABD=∠ACE
∠ABC=∠ACB
(等边对等角)
∠DBC=∠ECB
(等式性质)
夯实基础
A
B
C
D
3、如图,AB=AC,∠B=400,点D在BC上且∠DAC=500。求证:BD=CD
∵AB=AC,
∴∠B=∠C=400
∵∠B+∠C+∠BAC=1800
∴ ∠BAC=1000
∵∠DAC=500
∴∠BAD=500
∴∠DAC=∠BAD
∵AB=AC,AD平分∠BAC
∴BD=AD
证明:
(等边对等角)
(等式性质)
(等式性质)
(三线合一)
还有其他解法吗?
夯实基础
A
B
C
D
3、如图,AB=AC,∠B=400,点D在BC上且∠DAC=500。求证:BD=CD
要证:△ABD≌△ACD
要得:BD=CD
思路导航
需证:∠BAD=∠CAD=500
请你写出具体的证明过程!
(已有AB=AC,AD=AD)
如图,AB=AC,点D、E、F分别在BC、AB、AC上,且BD=CF,BE=CD,G是EF的中点,求证:DG┴EF
能力提升
A
B
C
D
G
E
F
∠1=∠2
要得:DG┴EF
思路导航
需证:△BDE≌△CFD
请你写出具体的证明过程!
(点G为EF中点)
需证:DEF为等腰三角形
要证:DE=DF
BD=CF
BE=CD
知识升华
讨论:怎样的两个等腰三角形全等?
②底角及底边对应相等
④顶角及腰对应相等
①两腰及底边对应相等
⑤底角及腰对应相等
③顶角及底边对应相等
(SSS)
(SAS)
或(AAS)
或(SAS)
(AAS)
(SAS)
或(AAS)
(AAS)
或(SAS)
轴对称图形
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线、和底边上的高
互相重合,简称“三线合 一”
等腰三角形
课内反思
5.3 简单的轴对称图形
北师版七(下)
等腰三角形的性质
(第一课时)
生活情景
生活情景
生活情景
生活情景
生活情景
以上图片都含有:
等腰三角形
定义:
两条边相等的三角形叫做等腰三角形.
如图AB=AC , 就是等腰三角形
等腰三角形的基本要素:
相等的两边叫做腰
另一边叫做底边
两腰的夹角叫做顶角
腰和底边的夹角叫做底角
A
B
C
腰
腰
底边
顶角
底角
底角
熟知概念
C
A
B
AC=BC
B
C
A
AB=CB
腰:
底边:
顶角:
底角:
腰:
底边:
顶角:
底角:
AC,BC
AB
A,
B
AB,CB
AC
B
A,
C
C
熟知概念
※在半透明的纸上,画一个等腰三角形,把它对折,
让两腰AB,AC重叠在一起,折痕为AD。
新知探究
B
A
C
D
A
B
C
D
※等腰三角形是轴对称图形吗?
对称轴是什么?
※从折叠过程中能发现什么?
重合的线段 重合的角
A
C
B
D
AB=AC
BD=CD
∠B = ∠C.
∠BAD = ∠CAD
∠ADB = ∠ADC= 90°
等腰三角形除了两腰相等以外,你还能发现它的其他相等的量吗
新知探究
(AD平分顶角)
(AD为底边的高)
(AD为底边的中线)
对于“∠B=∠C”这一结果如何表述成命题
等腰三角形两底角相等。
C
A
B
D
已知:如图△ABC中,AB=AC.
求证:∠B=∠C.
新知探究
等腰三角形两底角相等。
猜想:
是正确的吗?
定理:
分析:常用什么方法证明线段相等?
如何构造全等三角形?
全等三角形
作AD平分∠BAC
△ABD≌△ACD
(SAS)
∠B=∠C
作BC边中线AD
△ABD≌△ACD
(SSS)
∠B=∠C
新知探究
C
A
B
等腰三角形两底角相等。
定理:
(等边对等角)
在△ABC中,
∵AB=AC
∴∠B=∠C
(等边对等角)
重合的线段 重合的角
A
C
B
D
BD=CD
∠BAD = ∠CAD
∠ADB = ∠ADC= 90°
新知探究
(AD平分顶角)
(AD为底边的高)
(AD为底边的中线)
对于这三个结果如何表述成命题
等腰三角形底边上的中线、高及顶角角平分线互相重合。
已知:如图△ABC中,AB=AC,
求证:BD=CD,
新知探究
猜想:
是真命题吗?
定理:
等腰三角形底边上的中线、高及顶角角平分线互相重合。
AD⊥BC.
AD平分∠BAC
已知:如图△ABC中,AB=AC.
BD=CD.
求证:AD⊥BC,
AD平分∠BAC.
已知:如图△ABC中,AB=AC,
求证:BD=CD,
AD⊥BC
AD平分∠BAC.
(AAS)
(SSS)
C
A
B
D
(SAS)
C
D
B
A
①在ΔABC中,∵AB=AC,
∴ ∠B=∠C( )
等边对等角
(1)∵AB=AC,AD⊥BC,
∴∠____ = ∠____,___= ___
(2)∵AB=AC,AD是中线,
∴___⊥___ , ∠____ =∠____
(3)∵AB=AC,AD是角平分线,
∴___ ⊥___ ,___ =___
BAD CAD
BD CD
AD BC
AD BC
BD CD
②在△ABC中,
知识概括
BAD CAD
(“三线合一”)
(“三线合一”)
(“三线合一”)
例、如图,在△ABC中,AB = AC,D是BC边上的中点,∠BAC = 100°,求 ∠B和 ∠1的度数。
A
B
C
1
2
D
解:
∵∠BAC=1000,
∠B+∠C+∠BAC=1800
∴∠B+∠C=800
∵ AB = AC
∴ ∠B = ∠C =300
∵ AB=AC,D是BC边上的中点
∴∠1= ∠2=500
典例导学
(等式性质)
(等边对等角)
(三线合一)
还有什么不同的方法求∠B?
①等腰三角形一个角为70°,它的另外两个角为
___________________
②等腰三角形一个角为110°,它的另外两个角为________
70°,40°或55°,55°
35°,35°
夯实基础
1、填空
夯实基础
A
B
C
E
D
2、在△ABC中,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D、E。求证:∠DBC=∠ECB
∵AB=AC,
∴∠ABC=∠ACB
∵BD⊥AC,CE⊥AB
∴ ∠BDC=∠CEB=900
在△BEC和△CDB中
∠ABC=∠ACB
∠BDC=∠CEB
BC=CB
∴△ABD≌△ACD
∴∠DBC=∠EBC
证明:
(等边对等角)
(公共边)
还有其他解法吗?
夯实基础
A
B
C
E
D
2、在△ABC中,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D、E。求证:∠DBC=∠ECB
证明:
AB=AC
△ABD≌△ACE
(AAS)
∠ABD=∠ACE
∠ABC=∠ACB
(等边对等角)
∠DBC=∠ECB
(等式性质)
夯实基础
A
B
C
D
3、如图,AB=AC,∠B=400,点D在BC上且∠DAC=500。求证:BD=CD
∵AB=AC,
∴∠B=∠C=400
∵∠B+∠C+∠BAC=1800
∴ ∠BAC=1000
∵∠DAC=500
∴∠BAD=500
∴∠DAC=∠BAD
∵AB=AC,AD平分∠BAC
∴BD=AD
证明:
(等边对等角)
(等式性质)
(等式性质)
(三线合一)
还有其他解法吗?
夯实基础
A
B
C
D
3、如图,AB=AC,∠B=400,点D在BC上且∠DAC=500。求证:BD=CD
要证:△ABD≌△ACD
要得:BD=CD
思路导航
需证:∠BAD=∠CAD=500
请你写出具体的证明过程!
(已有AB=AC,AD=AD)
如图,AB=AC,点D、E、F分别在BC、AB、AC上,且BD=CF,BE=CD,G是EF的中点,求证:DG┴EF
能力提升
A
B
C
D
G
E
F
∠1=∠2
要得:DG┴EF
思路导航
需证:△BDE≌△CFD
请你写出具体的证明过程!
(点G为EF中点)
需证:DEF为等腰三角形
要证:DE=DF
BD=CF
BE=CD
知识升华
讨论:怎样的两个等腰三角形全等?
②底角及底边对应相等
④顶角及腰对应相等
①两腰及底边对应相等
⑤底角及腰对应相等
③顶角及底边对应相等
(SSS)
(SAS)
或(AAS)
或(SAS)
(AAS)
(SAS)
或(AAS)
(AAS)
或(SAS)
轴对称图形
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线、和底边上的高
互相重合,简称“三线合 一”
等腰三角形
课内反思
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
