9-1-2三角形的内角与外角和七年级数学下学期同步探讲练课件(华东师大版)
文档属性
| 名称 | 9-1-2三角形的内角与外角和七年级数学下学期同步探讲练课件(华东师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 775.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 00:00:00 | ||
图片预览





文档简介
(共12张PPT)
9.1.2三角形的内角与外角和
1
新知导入
在小学时,我们曾通过剪一剪、拼一拼的方法发现“一个三角形的三个内角恰好拼成一个平角;于是,得到如下结论:
三角形的内角和等于180°
2
新课讲授
问题
课本P76
现在我们尝试用说理的方式说明该结论的正确性。如图,已知△ABC,分别用∠1、∠2、∠3表示△ABC的三个内角,证明:∠1+∠2+∠3=180°
2
1
E
D
C
B
A
3
证明:作CD∥AB ,并延长BC到E,
∴∠1= ∠ACD(两直线平行,内错角相等)
∠2= ∠DCE (两直线平行,同位角相等)
∵∠3+ ∠ACD+ ∠DCE=180° (平角定义)
∴∠1+ ∠2 + ∠3=180° (等量代换)
总结
三角形的内角和等于180°
直角三角形的两个锐角互余
推论:
结论:
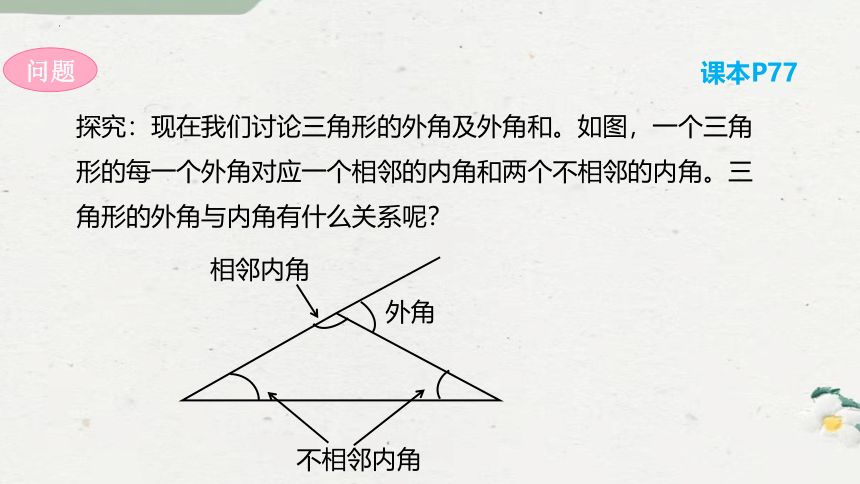
探究:现在我们讨论三角形的外角及外角和。如图,一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角。三角形的外角与内角有什么关系呢?
问题
课本P77
相邻内角
不相邻内角
外角
总结
三角形的一个外角+相邻内角=180°
三角形的一个外角等于与它不相邻的两个内角的和
三角形的一个外角大于任何一个与它不相邻的内角
三角形的外角和等于360°
课本P78
例题
例1、如图,D是△ABC的BC边上的一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°求:
(1)∠B的度数
课本P78
例题
例1、如图,D是△ABC的BC边上的一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°求:
(2)∠C的度数
(2)∵∠B+∠BAC+∠C=180°(三角形的内角和是180°)
∴∠C=180°-∠B-∠BAC(等式的性质)
=180°-40°-70°
=70°
3
课堂练习
1、判断
(1)用放大镜去看三角形,它的内角和就会变大。( )
(2) 一个三角形的三个内角度数可以是:80°、60°、40°。( )
(3)一个三角形中可以有两个内角是钝角( )
(4) 三角形的任何一个外角都大于其内角。( )
×
×
×
√
2、在△ABC中,∠A=60°,∠ B=40 ° 则∠C= .
3、在Rt△ABC中,其中一个锐角是45°,另一个锐角是 .
4、在△ABC中, ∠A :∠B:∠C=2:3:4,则∠A = ∠ B= . ∠ C= .
5、已知∠A=30°,∠B=20°,则∠BCD= .
A
C
B
D
100°
45°
60°
40°
80°
50°
4
拓展延伸
如图,在直角三角形ABC中,CD是斜边AB上的高,∠BCD=35°,
求:(1)∠EBC的度数;
(2)∠A的度数。
A
B
C
D
E
展示
9.1.2三角形的内角与外角和
1
新知导入
在小学时,我们曾通过剪一剪、拼一拼的方法发现“一个三角形的三个内角恰好拼成一个平角;于是,得到如下结论:
三角形的内角和等于180°
2
新课讲授
问题
课本P76
现在我们尝试用说理的方式说明该结论的正确性。如图,已知△ABC,分别用∠1、∠2、∠3表示△ABC的三个内角,证明:∠1+∠2+∠3=180°
2
1
E
D
C
B
A
3
证明:作CD∥AB ,并延长BC到E,
∴∠1= ∠ACD(两直线平行,内错角相等)
∠2= ∠DCE (两直线平行,同位角相等)
∵∠3+ ∠ACD+ ∠DCE=180° (平角定义)
∴∠1+ ∠2 + ∠3=180° (等量代换)
总结
三角形的内角和等于180°
直角三角形的两个锐角互余
推论:
结论:
探究:现在我们讨论三角形的外角及外角和。如图,一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角。三角形的外角与内角有什么关系呢?
问题
课本P77
相邻内角
不相邻内角
外角
总结
三角形的一个外角+相邻内角=180°
三角形的一个外角等于与它不相邻的两个内角的和
三角形的一个外角大于任何一个与它不相邻的内角
三角形的外角和等于360°
课本P78
例题
例1、如图,D是△ABC的BC边上的一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°求:
(1)∠B的度数
课本P78
例题
例1、如图,D是△ABC的BC边上的一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°求:
(2)∠C的度数
(2)∵∠B+∠BAC+∠C=180°(三角形的内角和是180°)
∴∠C=180°-∠B-∠BAC(等式的性质)
=180°-40°-70°
=70°
3
课堂练习
1、判断
(1)用放大镜去看三角形,它的内角和就会变大。( )
(2) 一个三角形的三个内角度数可以是:80°、60°、40°。( )
(3)一个三角形中可以有两个内角是钝角( )
(4) 三角形的任何一个外角都大于其内角。( )
×
×
×
√
2、在△ABC中,∠A=60°,∠ B=40 ° 则∠C= .
3、在Rt△ABC中,其中一个锐角是45°,另一个锐角是 .
4、在△ABC中, ∠A :∠B:∠C=2:3:4,则∠A = ∠ B= . ∠ C= .
5、已知∠A=30°,∠B=20°,则∠BCD= .
A
C
B
D
100°
45°
60°
40°
80°
50°
4
拓展延伸
如图,在直角三角形ABC中,CD是斜边AB上的高,∠BCD=35°,
求:(1)∠EBC的度数;
(2)∠A的度数。
A
B
C
D
E
展示
