9-2多边形的内角和与外角和七年级数学下学期同步探讲练课件(华东师大版)
文档属性
| 名称 | 9-2多边形的内角和与外角和七年级数学下学期同步探讲练课件(华东师大版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 773.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 09:29:12 | ||
图片预览




文档简介
9.2多边形的内角和与外角和
1
温故知新
1、三角形的概念?
2、三角形的内角和是多少度?
由三条不在同一直线上的线段首尾顺次连结组成的平面图形,叫做三角形。
180°
2
新课讲授
总结
课本P83
1、我们已经知道什么叫三角形,大家能说说什么叫四边形、五边形吗?
由四条不在同一直线上的线段首尾顺次连结组成的图形叫四边形
由五条不在同一直线上的线段首尾顺次连结组成的图形叫五边形
2、如果由n条不在同一直线上的线段首尾顺次连结组成的图形应该叫什么呢?
n边形,也是我们已经认识的多边形
我们现在研究的是凸多边形
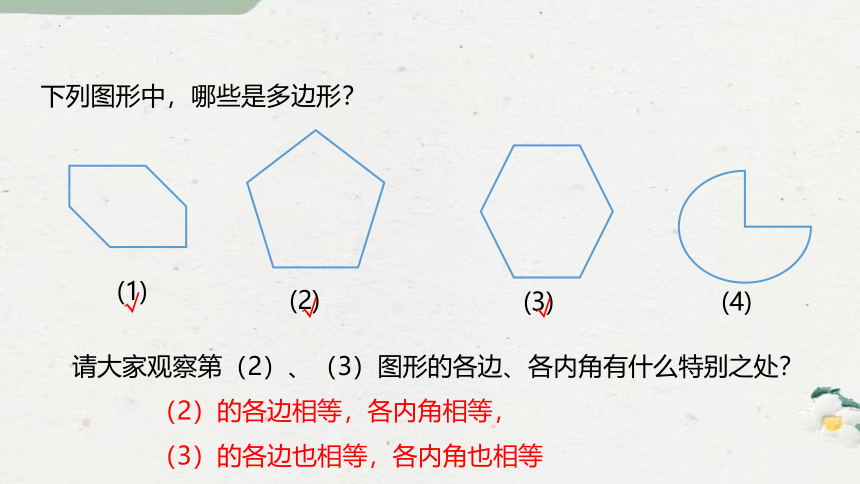
下列图形中,哪些是多边形?
(1)
(3)
(2)
(4)
√
√
√
请大家观察第(2)、(3)图形的各边、各内角有什么特别之处?
(2)的各边相等,各内角相等,
(3)的各边也相等,各内角也相等
总结
如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形。如:正三角形、正四边形、正五边形等。
课本P84
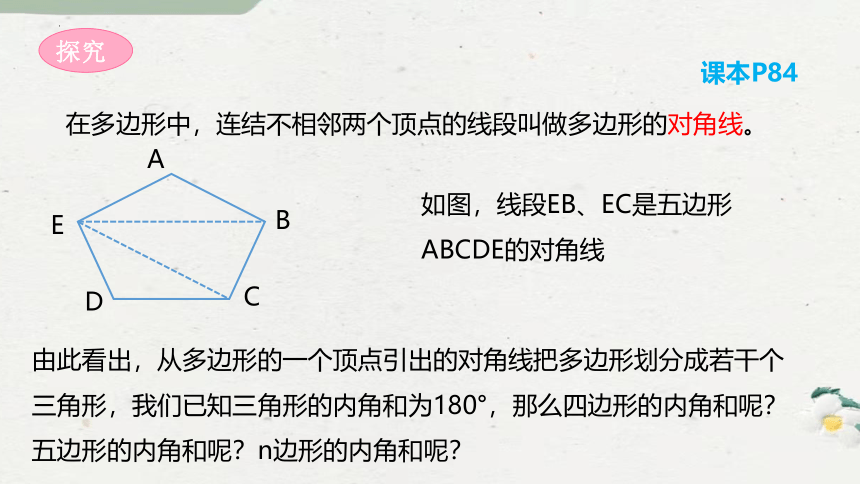
在多边形中,连结不相邻两个顶点的线段叫做多边形的对角线。
探究
A
E
D
C
B
如图,线段EB、EC是五边形ABCDE的对角线
由此看出,从多边形的一个顶点引出的对角线把多边形划分成若干个三角形,我们已知三角形的内角和为180°,那么四边形的内角和呢?五边形的内角和呢?n边形的内角和呢?
探究
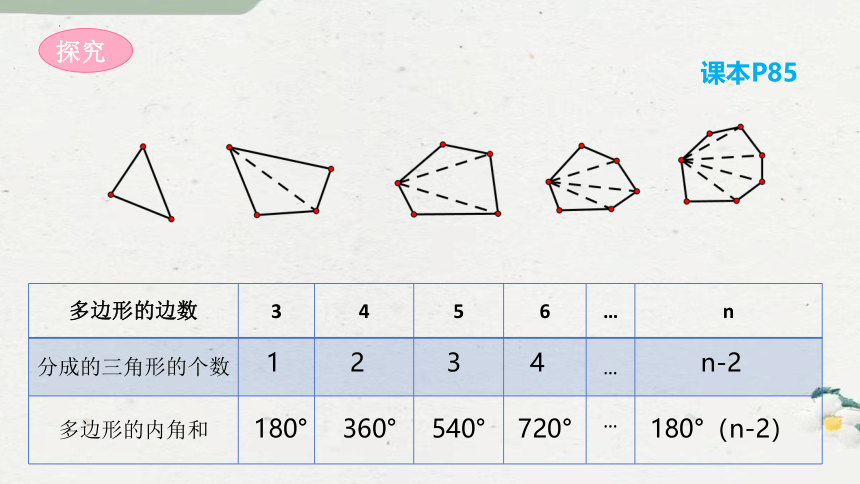
课本P85
{BDBED569-4797-4DF1-A0F4-6AAB3CD982D8}多边形的边数
3
4
5
6
…
n
分成的三角形的个数
…
多边形的内角和
…
360°
180°
540°
720°
180°(n-2)
1
2
3
4
n-2
总结
n边形的内角和为 180°(n-2)
例1:求八边形内角和。
课本P85
解:八边形的内角和为
(n-2)?180°=(8-2)?180°=1080°.
课本P85
例2:已知一个多边形的内角和等于2160°,求这个多边形的边数?
解: 设这个多边形的边数为n,根据题意,得
(n-2)?180°=2160°
解得 n=14
即这个多边形的边数为14。
探究
课本P86
与多边形的每个内角相邻的外角分别有两个,这两个外角是对顶角,从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和。
C
A
B
D
1
2
3
4
5
6
7
8
由图可知:
(∠1+∠5)+(∠2+∠6)+(∠3+∠7)+(∠4+∠8)=4x180°
所以∠1+∠2+∠3+∠4=4x180°-(∠5+∠6+∠7+∠8)
因为四边形的内角和为360°
所以∠5+∠6+∠7+∠8=360°
所以∠1+∠2+∠3+∠4=360°
探究
课本P87
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}多边形的边数
3
4
5
6
...
n
多边形的内角和与外角和的总和
...
多边形的内角和
...
多边形的外角和
...
540°
180°
360°
360°
360°
360°
360°
360°
540°
720°
720°
180°(n-2)
720°
1080°
180°n
总结
任意多边形的外角和都为 360°
课本P87
例3:一个多边形的每个外角都是72°,这个多边形是几边形?
解:设多边形的边数为n,根据题意,得
n ? 72°=360°
解得 n=5
因此,这个多边形是五边形
课本P87
例4:一个多边形的内角和等于它外角和的5倍,这个多边形是几边形?
解:设多边形的边数为n.根据题意,得
(n-2)? 180°=5 × 360°
解得 n=12
因此,这个多边形是十二边形
3
课堂练习
1、求下列图形中 x 的值。
x+65=x+x-5,
解得:x=70°
x+x+10°+60°+90°=360°解得:x=100°.
2、已知一个多边形的内角和等于720°,求这个多边形的边数。
解: 设这个多边形的边数为n,根据题意,得
(n-2)?180°=720°
解得 n=6
即这个多边形的边数为6。
3、已知一个正多边形的每个内角等于162°,求这个是正几边形?
解:因为该正多边形的每个内角等于162°
所以该正多边形的每个外角等于18°
因为多边形的外角和为360°
所以360°÷18°=20
故,这个是正二十边形
1
温故知新
1、三角形的概念?
2、三角形的内角和是多少度?
由三条不在同一直线上的线段首尾顺次连结组成的平面图形,叫做三角形。
180°
2
新课讲授
总结
课本P83
1、我们已经知道什么叫三角形,大家能说说什么叫四边形、五边形吗?
由四条不在同一直线上的线段首尾顺次连结组成的图形叫四边形
由五条不在同一直线上的线段首尾顺次连结组成的图形叫五边形
2、如果由n条不在同一直线上的线段首尾顺次连结组成的图形应该叫什么呢?
n边形,也是我们已经认识的多边形
我们现在研究的是凸多边形
下列图形中,哪些是多边形?
(1)
(3)
(2)
(4)
√
√
√
请大家观察第(2)、(3)图形的各边、各内角有什么特别之处?
(2)的各边相等,各内角相等,
(3)的各边也相等,各内角也相等
总结
如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形。如:正三角形、正四边形、正五边形等。
课本P84
在多边形中,连结不相邻两个顶点的线段叫做多边形的对角线。
探究
A
E
D
C
B
如图,线段EB、EC是五边形ABCDE的对角线
由此看出,从多边形的一个顶点引出的对角线把多边形划分成若干个三角形,我们已知三角形的内角和为180°,那么四边形的内角和呢?五边形的内角和呢?n边形的内角和呢?
探究
课本P85
{BDBED569-4797-4DF1-A0F4-6AAB3CD982D8}多边形的边数
3
4
5
6
…
n
分成的三角形的个数
…
多边形的内角和
…
360°
180°
540°
720°
180°(n-2)
1
2
3
4
n-2
总结
n边形的内角和为 180°(n-2)
例1:求八边形内角和。
课本P85
解:八边形的内角和为
(n-2)?180°=(8-2)?180°=1080°.
课本P85
例2:已知一个多边形的内角和等于2160°,求这个多边形的边数?
解: 设这个多边形的边数为n,根据题意,得
(n-2)?180°=2160°
解得 n=14
即这个多边形的边数为14。
探究
课本P86
与多边形的每个内角相邻的外角分别有两个,这两个外角是对顶角,从与每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和。
C
A
B
D
1
2
3
4
5
6
7
8
由图可知:
(∠1+∠5)+(∠2+∠6)+(∠3+∠7)+(∠4+∠8)=4x180°
所以∠1+∠2+∠3+∠4=4x180°-(∠5+∠6+∠7+∠8)
因为四边形的内角和为360°
所以∠5+∠6+∠7+∠8=360°
所以∠1+∠2+∠3+∠4=360°
探究
课本P87
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}多边形的边数
3
4
5
6
...
n
多边形的内角和与外角和的总和
...
多边形的内角和
...
多边形的外角和
...
540°
180°
360°
360°
360°
360°
360°
360°
540°
720°
720°
180°(n-2)
720°
1080°
180°n
总结
任意多边形的外角和都为 360°
课本P87
例3:一个多边形的每个外角都是72°,这个多边形是几边形?
解:设多边形的边数为n,根据题意,得
n ? 72°=360°
解得 n=5
因此,这个多边形是五边形
课本P87
例4:一个多边形的内角和等于它外角和的5倍,这个多边形是几边形?
解:设多边形的边数为n.根据题意,得
(n-2)? 180°=5 × 360°
解得 n=12
因此,这个多边形是十二边形
3
课堂练习
1、求下列图形中 x 的值。
x+65=x+x-5,
解得:x=70°
x+x+10°+60°+90°=360°解得:x=100°.
2、已知一个多边形的内角和等于720°,求这个多边形的边数。
解: 设这个多边形的边数为n,根据题意,得
(n-2)?180°=720°
解得 n=6
即这个多边形的边数为6。
3、已知一个正多边形的每个内角等于162°,求这个是正几边形?
解:因为该正多边形的每个内角等于162°
所以该正多边形的每个外角等于18°
因为多边形的外角和为360°
所以360°÷18°=20
故,这个是正二十边形
