9-3用正多边形铺设地板七年级数学下学期同步探讲练课件(华东师大版)
文档属性
| 名称 | 9-3用正多边形铺设地板七年级数学下学期同步探讲练课件(华东师大版) |  | |
| 格式 | pptx | ||
| 文件大小 | 752.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 09:31:33 | ||
图片预览





文档简介
(共13张PPT)
9.3.1用相同的正多边形铺设地板
1
新知导入
某些形状的地砖或瓷砖为什么能铺满地面而不留一点空隙?实际生活中,它们的形状大多是正多边形,就让我们一起去探究其中的奥秘吧!
2
新课讲授
问题
课本P89
使用给定的某种正多边形,它能否铺满地面,既不留下一丝空白,又不相互重叠呢?
与正多边形的内角大小有关
课本P89
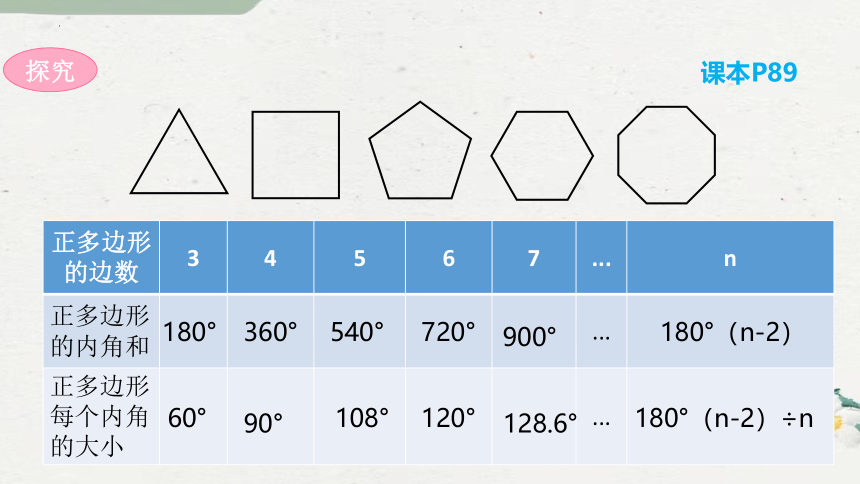
探究
正多边形的边数 3 4 5 6 7 ... n
正多边形的内角和 ...
正多边形每个内角的大小 ...
180°(n-2)
180°(n-2)÷n
180°
360°
540°
720°
900°
60°
90°
108°
120°
128.6°
探究
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面。
正三角形:每个内角是60°,360°÷60°=6(能铺满)
正四边形:每个内角是90°,360°÷90°=4(能铺满)
正五边形:每个内角是108°,360°÷108°=3.333333...(不能铺满)
总结
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。
有时候为了图案更加丰富且有特色,我们会用多种不同的正多边形组合使用,如何组合能铺满地面,既不留下一丝空白,又不相互重叠呢?
课本P90
探究
用正三角形和正六边形可以吗?
正三角形的每个内角是60°,正六边形的每个内角是120°
因为60°x2+120°x2=360°
所以用正三角形和正六边形可以铺满地面
用正十二边形、正六边形和正方形可以铺满吗?
探究
正十二边形的每个内角是150°,正六边形的每个内角是120°,正方形的每个内角是90°
因为150°+120°+90°=360°
所以用正十二边形、正六边形和正方形可以铺满地面
总结2
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。
3
课堂练习
1、下列不能够单独进行平面镶嵌地面的多边形是( )
A、三角形 B、四边形 C、正五边形 D、正六边形
2、下列正多边形的组合不能铺满地面的是( )
A、正三角形和正六边形 B、正三角形和正方形
C、正方形和正八边形 D、正六边形和正八边形
C
D
3、如图所示,三个相同的正n边形拼成的无缝隙、不重叠的一部分,则n的值为( )。
6
4
拓展延伸
用正三角形和正六边形的瓷砖铺地面,在一个顶点周围可以有几个正三角形和几个正六边形?并说明理由。
解:设在一个顶点周围有m个正三角形的角,n个正六边形的角。
由题意得 m×60°+ n×120°= 360°
即 m+ 2n= 6 满足题意的正整数解为
m=4
n=1
m=2
n=2
或
答:在一个顶点周围有4个正三角形和1个正六边形
或者在一个顶点周围有2个正三角形和2个正六边形
9.3.1用相同的正多边形铺设地板
1
新知导入
某些形状的地砖或瓷砖为什么能铺满地面而不留一点空隙?实际生活中,它们的形状大多是正多边形,就让我们一起去探究其中的奥秘吧!
2
新课讲授
问题
课本P89
使用给定的某种正多边形,它能否铺满地面,既不留下一丝空白,又不相互重叠呢?
与正多边形的内角大小有关
课本P89
探究
正多边形的边数 3 4 5 6 7 ... n
正多边形的内角和 ...
正多边形每个内角的大小 ...
180°(n-2)
180°(n-2)÷n
180°
360°
540°
720°
900°
60°
90°
108°
120°
128.6°
探究
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角时,就可以铺满地面。
正三角形:每个内角是60°,360°÷60°=6(能铺满)
正四边形:每个内角是90°,360°÷90°=4(能铺满)
正五边形:每个内角是108°,360°÷108°=3.333333...(不能铺满)
总结
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。
有时候为了图案更加丰富且有特色,我们会用多种不同的正多边形组合使用,如何组合能铺满地面,既不留下一丝空白,又不相互重叠呢?
课本P90
探究
用正三角形和正六边形可以吗?
正三角形的每个内角是60°,正六边形的每个内角是120°
因为60°x2+120°x2=360°
所以用正三角形和正六边形可以铺满地面
用正十二边形、正六边形和正方形可以铺满吗?
探究
正十二边形的每个内角是150°,正六边形的每个内角是120°,正方形的每个内角是90°
因为150°+120°+90°=360°
所以用正十二边形、正六边形和正方形可以铺满地面
总结2
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。
3
课堂练习
1、下列不能够单独进行平面镶嵌地面的多边形是( )
A、三角形 B、四边形 C、正五边形 D、正六边形
2、下列正多边形的组合不能铺满地面的是( )
A、正三角形和正六边形 B、正三角形和正方形
C、正方形和正八边形 D、正六边形和正八边形
C
D
3、如图所示,三个相同的正n边形拼成的无缝隙、不重叠的一部分,则n的值为( )。
6
4
拓展延伸
用正三角形和正六边形的瓷砖铺地面,在一个顶点周围可以有几个正三角形和几个正六边形?并说明理由。
解:设在一个顶点周围有m个正三角形的角,n个正六边形的角。
由题意得 m×60°+ n×120°= 360°
即 m+ 2n= 6 满足题意的正整数解为
m=4
n=1
m=2
n=2
或
答:在一个顶点周围有4个正三角形和1个正六边形
或者在一个顶点周围有2个正三角形和2个正六边形
