沪科版七年级下册 10.2 第1课时平行线及平行公理 课件(共29张)
文档属性
| 名称 | 沪科版七年级下册 10.2 第1课时平行线及平行公理 课件(共29张) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-04 19:48:04 | ||
图片预览





文档简介
(共29张PPT)
沪科版七年级下册
10.2 平行线的判定
平行线定义及平行公理
4.结合生活情境,经历了解两条直线平行以及画平行线的过程对周围环境中与平行线有关的事物有好奇心,获得成功的体验。
教学目标
2. 会利用三角尺和直尺过直线外一点画已知直线平行线。
1.了解平面上两条直线的平行关系;理解平面内两条直线平行的概念和表示方法
3.理解并掌握平行线的两个基本事实
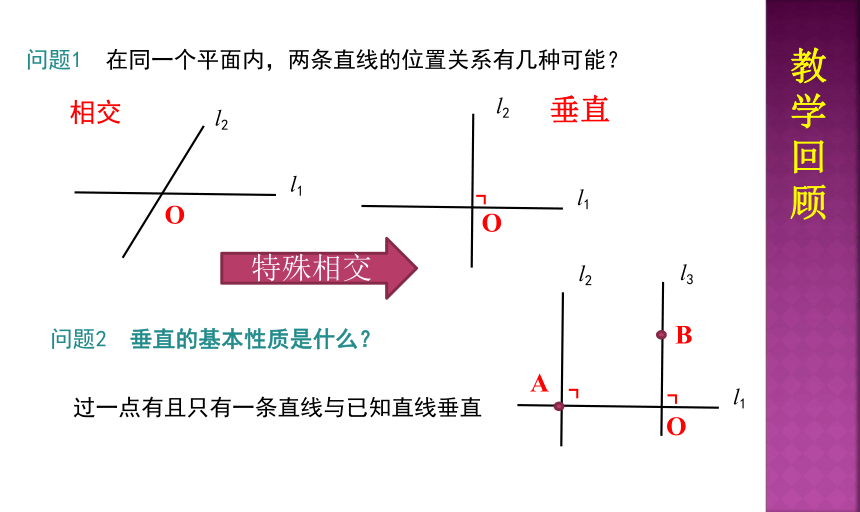
问题1 在同一个平面内,两条直线的位置关系有几种可能?
l1
教学回顾
l1
l2
┓
相交
垂直
特殊相交
问题2 垂直的基本性质是什么?
过一点有且只有一条直线与已知直线垂直
l1
l2
l3
A
B
O
O
O
l2
┓
┓
人家兄弟手拉手,
我们兄弟不碰头。
火车在咱肩上跑,
高压电咱肩上流。
(打一图形)
铁轨
猜一猜
教学导入
讨论
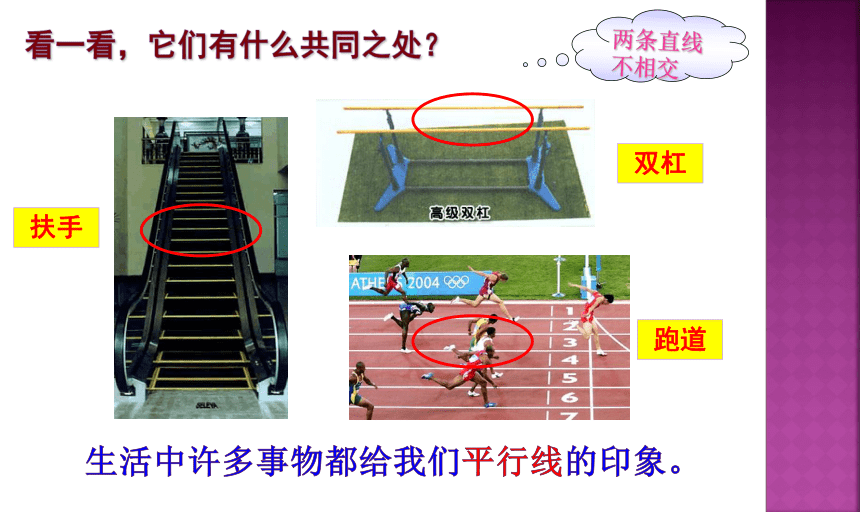
你见过生活中类似的现象吗?与同学们交流!
扶手
双杠
跑道
两条直线不相交
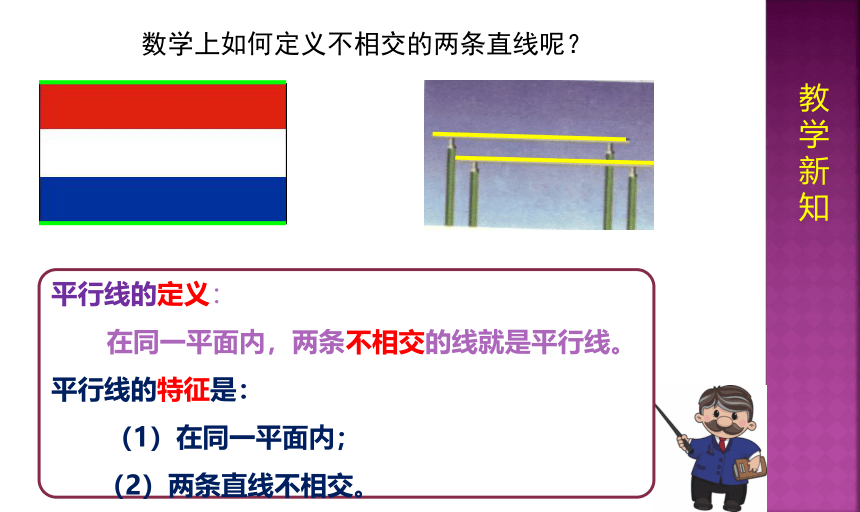
数学上如何定义不相交的两条直线呢?
平行线的定义:
在同一平面内,两条不相交的线就是平行线。
平行线的特征是:
(1)在同一平面内;
(2)两条直线不相交。
教学新知
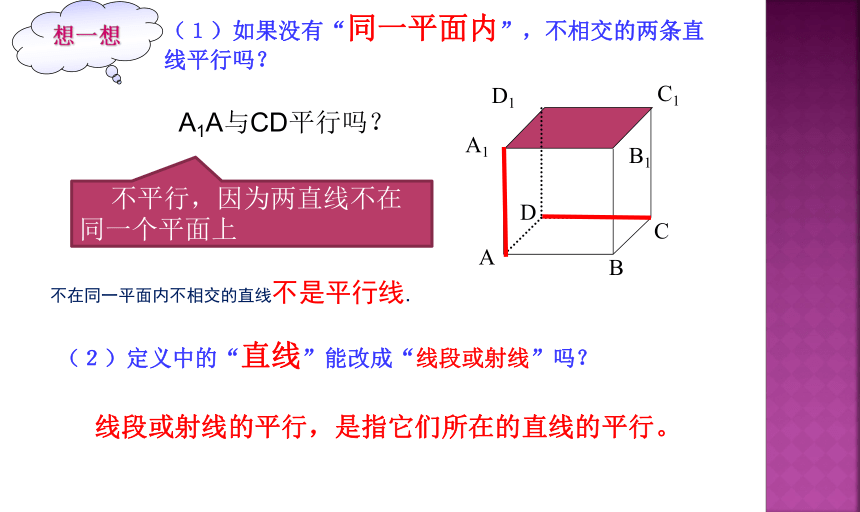
(1)如果没有“同一平面内”,不相交的两条直线平行吗?
(2)定义中的“直线”能改成“线段或射线”吗?
想一想
线段或射线的平行,是指它们所在的直线的平行。
A
B
C
D
A1
B1
C1
D1
A1A与CD平行吗?
不平行,因为两直线不在同一个平面上
不在同一平面内不相交的直线不是平行线.
(1)
(2)
(3)
平行线的定义包含三层意思:
(1)“在同一平面内”是前提条件,
(2)“不相交”就是说两条直线没有交点,
(3)平行线指的是“两条直线”而不是两条射线或两条线段.
注意:
平行用符号“∥”表示,
如:直线AB与直线CD平行,
记作:AB∥CD,读作“AB平行于CD”。
注意:平行线是相互的,使用平行符号“∥”时, 可以写成:AB∥CD,
也可写成:CD∥AB。
A
B
C
D
定义
在同一平面内,不相交的两条直线。
符号
图形
读法
A
B
C
D
AB∥CD
直线AB平行于直线CD
直线a平行于直线b
a
b
我们通常用符号“//”表示平行。
a∥b
同一平面内两直线有几种位置关系?
平行
相交
垂直
相交但不垂直
a
b
a⊥b
a ∥b
a
b
b
a
在同一平面内,两直线的位置关系有平行与相交两种。
想一想
结论
下列说法是否正确,并说明理由.
①不相交的两条直线是平行线.
②在同一平面内,两条不相交的线段是平行线.
③过一点可以而且只可以画一条直线与已知直线平行.
(×)
(×)
(×)
如图,已知直线AB和直线外一点p,能利用三角尺和直尺,经过点p,画出与直线a平行的直线吗?试一试,并与同学交流。
B
.P
A
●
一、落
二、贴
三、推
四、画
P
推平行线法
A
B
推平行线的画法:
把三角尺的一边落在直线上
紧靠三角尺的另一边放一直尺
把三角尺沿直尺的边推到三角尺
的第一边恰好经过点P的位置
沿三角尺的这一边画直线
·
A
B
P
1落:把三角尺的一边落在直线上
2靠:紧靠三角尺的另一边放一直尺
3推:把三角尺沿直尺的边推到三角尺的第一边恰好经过点P的位置
4画:沿三角尺的这一边画直线
过直线AB外一点P作直线AB的平行线,看看你能作出吗?能作出几条?
·
A
B
P
动手实践
由以上的实践你发现了什么?说说看
平行线的基本性质:
性质1:经过直线外一点,有且只有一条直线与已知直线平行。
说明:
人们在长期实践中总结出来的结论叫基本事实,也称为公理,它可以作为以后推理的依据.
平行公理
(唯一性)
三条直线a、b、c。如果a//c,b//c,直线a与b有什么关系?
F
E
b
a
假设a与b相交,设a与b相交于O
∵ a//c,b//c
∴过点O就有两条直线ab都与c平行。
根据平行公理,这是不可能的
也就是说,a与b不能相交,只能平行。
c
思 考:
O
平行公理的推论
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行
几何语言表达:
∵a//c , c//b(已知)
a//b(平行于同一条直线的两条直线平行)
平行于同一条直线的两条直线平行。
简单地说
a
b
c
平行线的传递性
A
B
P
如图,在⊿ ABC中,P是AC边上一点.过点P分别画AB,BC的平行线.
C
D
新知应用
A
B
P
如图,中,P是AC边上一点.过点P分别画AB,BC的在⊿ ABC平行线.
c
D
E
∴PD、PE就是所要画的直线。
新知应用
1、下列说法中正确的是( )
A、在同一平面内,两条直线的位置关系有相交、垂 直、平行。
B、在同一平面内如果两条线段不相交,那么这两条线段平行。
C、在同一平面内,不相交的两条射线是平行线。
D、在同一平面内,不相交的两直线是平行线。
D
2、下列说法中错误的个数是:( )
①一条直线的平行线只有一条
② 过一点与已知直线平行的直线有且只有一条
③过直线外一点与这条已知直线平行的直线有且只有一条
A 、0 B 、1 C 、2 D、3
C
练习
课堂练习
3、同一平面内,三条直线的交点可以有 个.
0或1或2或3
4、对于同一平面内的直线a、b、c,如果a∥b,c与a相交,那么c与b是位置关系是 。
练习
相交
课堂练习
5、完成下列推理,并在括号内注明理由。
(1)如图1所示,因为AB // DE,BC // DE(已知)。
所以A,B,C三点___________( )
(2)如图2所示,因为AB // CD,CD // EF(已知),所以
________ // _________( )
·
·
·
A
D
E
B
C
图 1
A
B
C
D
E
F
图 2
在同一直线上
经过直线外一点,有且只有一条直线与这条直线平行
AB
EF
平行于同一条直线的两直线平行
课堂练习
6、一个长方体如图,
(1)和AA′平行的棱有多少条?请用符号把它们表示出来。
A′
B′
C′
D′
(1)和AA′平行的棱有3条:
BB′∥AA′,
CC′∥AA′,
DD′∥AA′。
(2)用符号表示下列两棱的位置关系:
A ′ B ′ ____AB, AA ′ ____AB ,
A ′ D ′ ____C ′ D ′ , AD___ _BC
∥
⊥
⊥
∥
课堂练习
④ 过一点有且只有一条直线与己知直线平行。( )
√
×
√
×
在同一平面内,下列说法中是否正确
① 过两点有且只有一条直线.( )
② 两条不同的直线有且只有一个公共点.( )
③ 过一点有且只有一条直线与己知直线垂直。( )
拓展练习
归纳小结
只有一个公共点的两条直线
同一个平面内不相交的两条直线
a
b
O
直线a 、b交于O
a
b
a //b
对顶角相等
平行公理
邻补角互补
平行公理推论:
∵ a ∥ c,b ∥ c ;
∴ a ∥ b
b
a
c
平行与相交
同一平面内两直线位置关系
推平行线的画法:
一落
二靠
三推
四画
·
平行线的画法:
归纳小结
沪科版七年级下册
10.2 平行线的判定
平行线定义及平行公理
4.结合生活情境,经历了解两条直线平行以及画平行线的过程对周围环境中与平行线有关的事物有好奇心,获得成功的体验。
教学目标
2. 会利用三角尺和直尺过直线外一点画已知直线平行线。
1.了解平面上两条直线的平行关系;理解平面内两条直线平行的概念和表示方法
3.理解并掌握平行线的两个基本事实
问题1 在同一个平面内,两条直线的位置关系有几种可能?
l1
教学回顾
l1
l2
┓
相交
垂直
特殊相交
问题2 垂直的基本性质是什么?
过一点有且只有一条直线与已知直线垂直
l1
l2
l3
A
B
O
O
O
l2
┓
┓
人家兄弟手拉手,
我们兄弟不碰头。
火车在咱肩上跑,
高压电咱肩上流。
(打一图形)
铁轨
猜一猜
教学导入
讨论
你见过生活中类似的现象吗?与同学们交流!
扶手
双杠
跑道
两条直线不相交
数学上如何定义不相交的两条直线呢?
平行线的定义:
在同一平面内,两条不相交的线就是平行线。
平行线的特征是:
(1)在同一平面内;
(2)两条直线不相交。
教学新知
(1)如果没有“同一平面内”,不相交的两条直线平行吗?
(2)定义中的“直线”能改成“线段或射线”吗?
想一想
线段或射线的平行,是指它们所在的直线的平行。
A
B
C
D
A1
B1
C1
D1
A1A与CD平行吗?
不平行,因为两直线不在同一个平面上
不在同一平面内不相交的直线不是平行线.
(1)
(2)
(3)
平行线的定义包含三层意思:
(1)“在同一平面内”是前提条件,
(2)“不相交”就是说两条直线没有交点,
(3)平行线指的是“两条直线”而不是两条射线或两条线段.
注意:
平行用符号“∥”表示,
如:直线AB与直线CD平行,
记作:AB∥CD,读作“AB平行于CD”。
注意:平行线是相互的,使用平行符号“∥”时, 可以写成:AB∥CD,
也可写成:CD∥AB。
A
B
C
D
定义
在同一平面内,不相交的两条直线。
符号
图形
读法
A
B
C
D
AB∥CD
直线AB平行于直线CD
直线a平行于直线b
a
b
我们通常用符号“//”表示平行。
a∥b
同一平面内两直线有几种位置关系?
平行
相交
垂直
相交但不垂直
a
b
a⊥b
a ∥b
a
b
b
a
在同一平面内,两直线的位置关系有平行与相交两种。
想一想
结论
下列说法是否正确,并说明理由.
①不相交的两条直线是平行线.
②在同一平面内,两条不相交的线段是平行线.
③过一点可以而且只可以画一条直线与已知直线平行.
(×)
(×)
(×)
如图,已知直线AB和直线外一点p,能利用三角尺和直尺,经过点p,画出与直线a平行的直线吗?试一试,并与同学交流。
B
.P
A
●
一、落
二、贴
三、推
四、画
P
推平行线法
A
B
推平行线的画法:
把三角尺的一边落在直线上
紧靠三角尺的另一边放一直尺
把三角尺沿直尺的边推到三角尺
的第一边恰好经过点P的位置
沿三角尺的这一边画直线
·
A
B
P
1落:把三角尺的一边落在直线上
2靠:紧靠三角尺的另一边放一直尺
3推:把三角尺沿直尺的边推到三角尺的第一边恰好经过点P的位置
4画:沿三角尺的这一边画直线
过直线AB外一点P作直线AB的平行线,看看你能作出吗?能作出几条?
·
A
B
P
动手实践
由以上的实践你发现了什么?说说看
平行线的基本性质:
性质1:经过直线外一点,有且只有一条直线与已知直线平行。
说明:
人们在长期实践中总结出来的结论叫基本事实,也称为公理,它可以作为以后推理的依据.
平行公理
(唯一性)
三条直线a、b、c。如果a//c,b//c,直线a与b有什么关系?
F
E
b
a
假设a与b相交,设a与b相交于O
∵ a//c,b//c
∴过点O就有两条直线ab都与c平行。
根据平行公理,这是不可能的
也就是说,a与b不能相交,只能平行。
c
思 考:
O
平行公理的推论
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行
几何语言表达:
∵a//c , c//b(已知)
a//b(平行于同一条直线的两条直线平行)
平行于同一条直线的两条直线平行。
简单地说
a
b
c
平行线的传递性
A
B
P
如图,在⊿ ABC中,P是AC边上一点.过点P分别画AB,BC的平行线.
C
D
新知应用
A
B
P
如图,中,P是AC边上一点.过点P分别画AB,BC的在⊿ ABC平行线.
c
D
E
∴PD、PE就是所要画的直线。
新知应用
1、下列说法中正确的是( )
A、在同一平面内,两条直线的位置关系有相交、垂 直、平行。
B、在同一平面内如果两条线段不相交,那么这两条线段平行。
C、在同一平面内,不相交的两条射线是平行线。
D、在同一平面内,不相交的两直线是平行线。
D
2、下列说法中错误的个数是:( )
①一条直线的平行线只有一条
② 过一点与已知直线平行的直线有且只有一条
③过直线外一点与这条已知直线平行的直线有且只有一条
A 、0 B 、1 C 、2 D、3
C
练习
课堂练习
3、同一平面内,三条直线的交点可以有 个.
0或1或2或3
4、对于同一平面内的直线a、b、c,如果a∥b,c与a相交,那么c与b是位置关系是 。
练习
相交
课堂练习
5、完成下列推理,并在括号内注明理由。
(1)如图1所示,因为AB // DE,BC // DE(已知)。
所以A,B,C三点___________( )
(2)如图2所示,因为AB // CD,CD // EF(已知),所以
________ // _________( )
·
·
·
A
D
E
B
C
图 1
A
B
C
D
E
F
图 2
在同一直线上
经过直线外一点,有且只有一条直线与这条直线平行
AB
EF
平行于同一条直线的两直线平行
课堂练习
6、一个长方体如图,
(1)和AA′平行的棱有多少条?请用符号把它们表示出来。
A′
B′
C′
D′
(1)和AA′平行的棱有3条:
BB′∥AA′,
CC′∥AA′,
DD′∥AA′。
(2)用符号表示下列两棱的位置关系:
A ′ B ′ ____AB, AA ′ ____AB ,
A ′ D ′ ____C ′ D ′ , AD___ _BC
∥
⊥
⊥
∥
课堂练习
④ 过一点有且只有一条直线与己知直线平行。( )
√
×
√
×
在同一平面内,下列说法中是否正确
① 过两点有且只有一条直线.( )
② 两条不同的直线有且只有一个公共点.( )
③ 过一点有且只有一条直线与己知直线垂直。( )
拓展练习
归纳小结
只有一个公共点的两条直线
同一个平面内不相交的两条直线
a
b
O
直线a 、b交于O
a
b
a //b
对顶角相等
平行公理
邻补角互补
平行公理推论:
∵ a ∥ c,b ∥ c ;
∴ a ∥ b
b
a
c
平行与相交
同一平面内两直线位置关系
推平行线的画法:
一落
二靠
三推
四画
·
平行线的画法:
归纳小结
