6.1.1向量的概念 课件(共16张PPT)
文档属性
| 名称 | 6.1.1向量的概念 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 12:58:00 | ||
图片预览





文档简介
(共16张PPT)
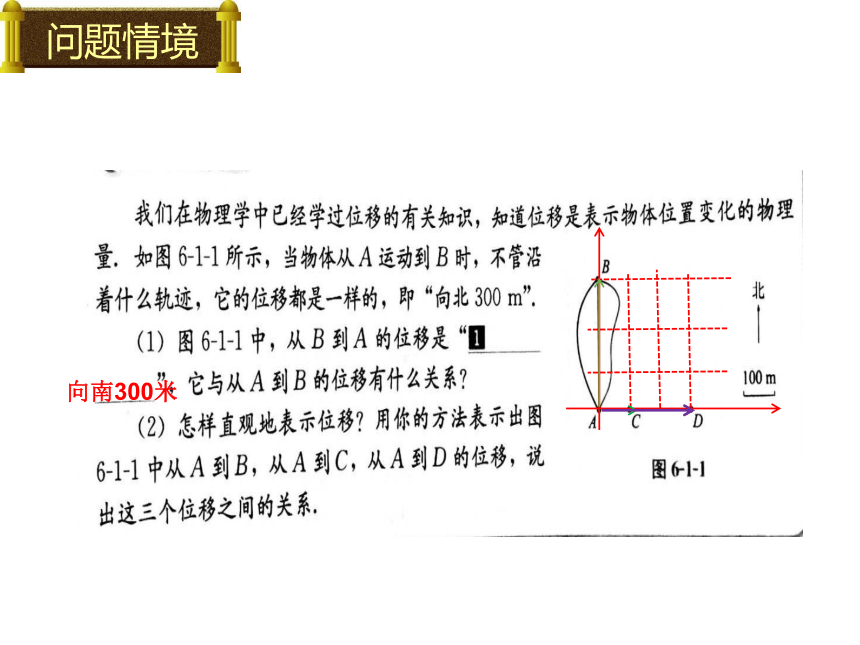
问题情境
向南300米
一.向量的相关概念
建构数学
路程
位移
只有大小
既有大小又有方向
矢量
在你学过的量中,哪些是标量,哪些是向量?
标量
向量
1.向量的定义:既有大小又有方向的量。
学生活动
判断下列说法是否正确:
由于零上温度可以用正数来表示,零下温度可以用负数来表示,所以温度是向量.
错误,因为温度没有方向.
坐标平面上的x轴和y轴是向量.
错误,因为无法刻画x轴和y轴的大小.
“大小”和“方向”是向量的两个重要方面!
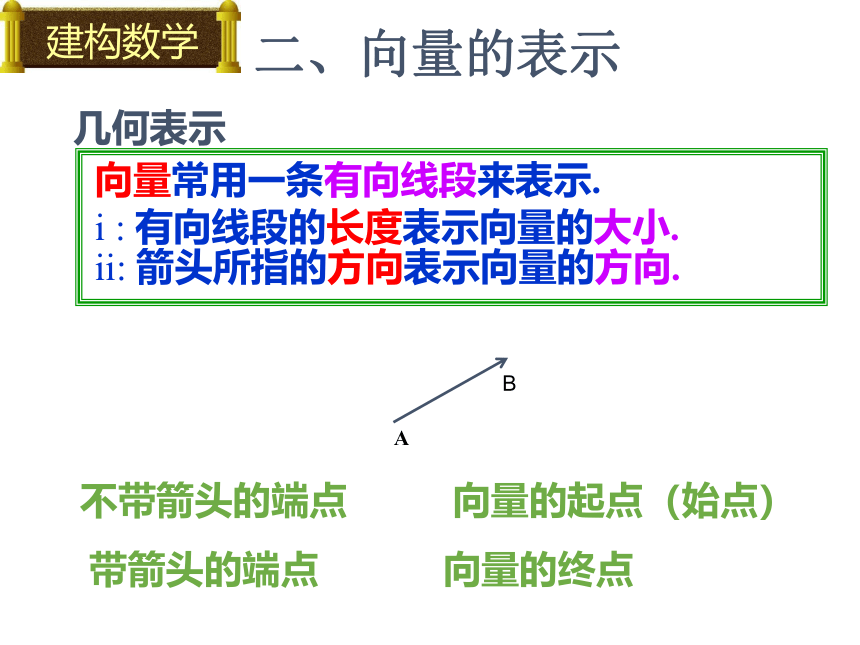
二、向量的表示
建构数学
i : 有向线段的长度表示向量的大小.
ii: 箭头所指的方向表示向量的方向.
向量常用一条有向线段来表示.
几何表示
不带箭头的端点 向量的起点(始点)
带箭头的端点 向量的终点
A
B
建构数学
带箭头的小写字母
向量可以用有向线段的起点和终点字母表示,
字母表示
在印刷时,常用粗黑体小写字母 a , b , c 来表示; 手写时则可用带箭头的小写字母 来表示.
向量的大小(模)
记作 | | .
建构数学
思考:
建构数学
零向量:起点和终点相同的向量,记作 .
任意方向都可作为零向量的方向
两个特殊的向量
建构数学
单位向量:模长为1 个单位长度的向量,叫做单位向量 .
思考:
单位向量唯一吗
平面直角坐标系内,所有起点在原点的单位向量,它们终点的轨迹是什么图形
学生活动
(2)、指出方向相同或者相反的向量
(1)、直接读出向量
(3) 指出每个向量的模
设图中小正形的边长为1
A
B
C
D
建构数学
三、向量的关系
平行向量: 方向相同 或相反 的非零向量
叫做平行向量。 (共线向量)
相等向量: 大小相等 且方向相同 的向量
叫做相等向量 。
建构数学
三、向量的关系
规定:零向量与任一向量平行.
表示平行向量的有向线段所在直线“平行”或“重合”.
思考 :
相等向量一定是平行向量吗
平行向量一定是相等向量吗
不是
是
例1、如图,O是正方形ABCD对角线的交点,四边形OAED,OCFB都是正方形,在图中所示的向量中:
巩固练习
(1)与 相等的向量为 ;
(2)与 共线的向量为 ;
(3)与 的模相等的向量为 ;
(4)向量 与 是否相等?答 .
例2.根据下列小题的条件,分别判断四边形ABCD
的形状:
(1) ; (2) 且
(2)四边形ABCD是菱形。
(1)四边形ABCD是平行四边形。
课堂小结
向量
向量
向量的大小
(模)
向量的方向
向量的表示
零向量
单位向量
平行向量
(共线向量)
问题情境
向南300米
一.向量的相关概念
建构数学
路程
位移
只有大小
既有大小又有方向
矢量
在你学过的量中,哪些是标量,哪些是向量?
标量
向量
1.向量的定义:既有大小又有方向的量。
学生活动
判断下列说法是否正确:
由于零上温度可以用正数来表示,零下温度可以用负数来表示,所以温度是向量.
错误,因为温度没有方向.
坐标平面上的x轴和y轴是向量.
错误,因为无法刻画x轴和y轴的大小.
“大小”和“方向”是向量的两个重要方面!
二、向量的表示
建构数学
i : 有向线段的长度表示向量的大小.
ii: 箭头所指的方向表示向量的方向.
向量常用一条有向线段来表示.
几何表示
不带箭头的端点 向量的起点(始点)
带箭头的端点 向量的终点
A
B
建构数学
带箭头的小写字母
向量可以用有向线段的起点和终点字母表示,
字母表示
在印刷时,常用粗黑体小写字母 a , b , c 来表示; 手写时则可用带箭头的小写字母 来表示.
向量的大小(模)
记作 | | .
建构数学
思考:
建构数学
零向量:起点和终点相同的向量,记作 .
任意方向都可作为零向量的方向
两个特殊的向量
建构数学
单位向量:模长为1 个单位长度的向量,叫做单位向量 .
思考:
单位向量唯一吗
平面直角坐标系内,所有起点在原点的单位向量,它们终点的轨迹是什么图形
学生活动
(2)、指出方向相同或者相反的向量
(1)、直接读出向量
(3) 指出每个向量的模
设图中小正形的边长为1
A
B
C
D
建构数学
三、向量的关系
平行向量: 方向相同 或相反 的非零向量
叫做平行向量。 (共线向量)
相等向量: 大小相等 且方向相同 的向量
叫做相等向量 。
建构数学
三、向量的关系
规定:零向量与任一向量平行.
表示平行向量的有向线段所在直线“平行”或“重合”.
思考 :
相等向量一定是平行向量吗
平行向量一定是相等向量吗
不是
是
例1、如图,O是正方形ABCD对角线的交点,四边形OAED,OCFB都是正方形,在图中所示的向量中:
巩固练习
(1)与 相等的向量为 ;
(2)与 共线的向量为 ;
(3)与 的模相等的向量为 ;
(4)向量 与 是否相等?答 .
例2.根据下列小题的条件,分别判断四边形ABCD
的形状:
(1) ; (2) 且
(2)四边形ABCD是菱形。
(1)四边形ABCD是平行四边形。
课堂小结
向量
向量
向量的大小
(模)
向量的方向
向量的表示
零向量
单位向量
平行向量
(共线向量)
