第一章乘法公式的应用复习学案

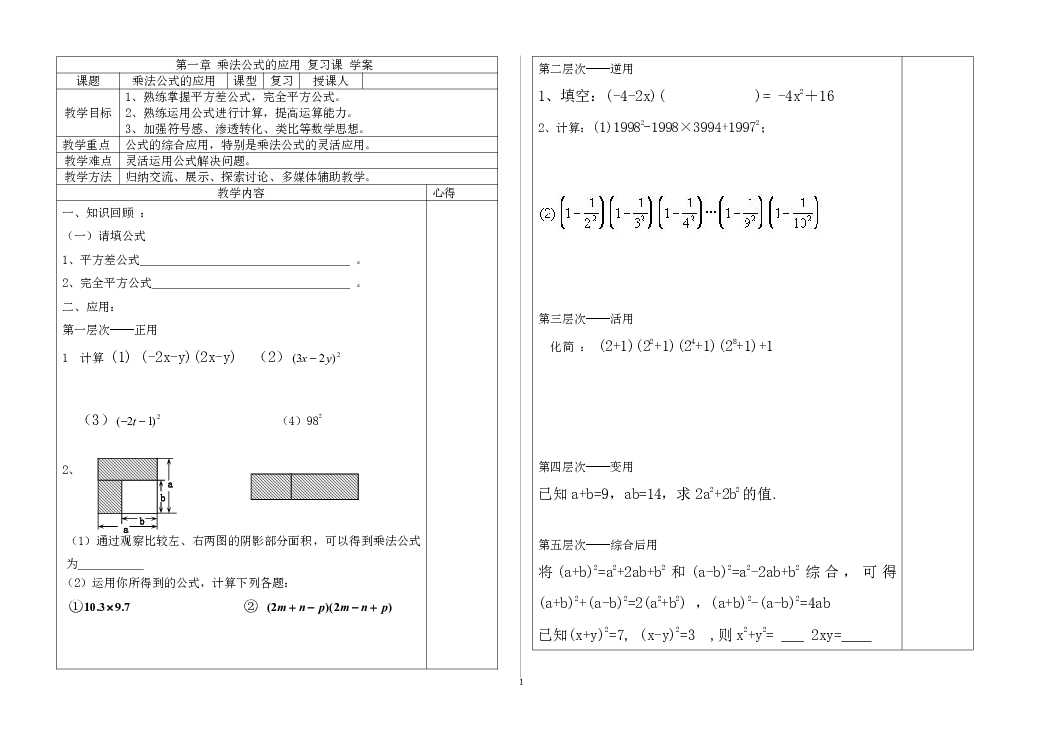
第一章 乘法公式的应用 复习课 学案
课题
乘法公式的应用
课型
复习
授课人
教学目标
1、熟练掌握平方差公式，完全平方公式。
2、熟练运用公式进行计算，提高运算能力。
3、加强符号感、渗透转化、类比等数学思想。
教学重点
公式的综合应用，特别是乘法公式的灵活应用。
教学难点
灵活运用公式解决问题。
教学方法
归纳交流、展示、探索讨论、多媒体辅助教学。
教学内容
心得
一、知识回顾 ：
（一）请填公式
1、平方差公式 。
2、完全平方公式 。
二、应用：
第一层次──正用
1 计算 (1) (-2x-y)(2x-y) （2）

（3） （4）982
2、

（1）通过观察比较左、右两图的阴影部分面积，可以得到乘法公式为
（2）运用你所得到的公式，计算下列各题：
①　 ②
第二层次──逆用
1、填空：(-4-2x)( )= -4x2＋16
2、计算：(1)19982-1998×3994+19972；


第三层次──活用
化简 ： (2+1)(22+1)(24+1)(28+1)+1
第四层次──变用
已知a+b=9，ab=14，求2a2+2b2的值．
第五层次──综合后用
将(a+b)2=a2+2ab+b2和(a-b)2=a2-2ab+b2综合，可得 (a+b)2+(a-b)2=2(a2+b2) ，(a+b)2-(a-b)2=4ab
已知(x+y)2=7, (x-y)2=3 ,则x2+y2= 2xy=
三、反馈练习
（一）、单选
1下列算式能用平方差公式计算的是（ ）
A.（2a＋b）（2b－a） B.
C.（3x－y）（－3x＋y） D.（－m－n）（－m＋n）
2、若 4a2-2ka+9是一个完全平方的展开形式，试求k的值：（ ）
A、12 B、±6 C、6 D、±12
3.│5x-2y│·│2y-5x│的结果是 ( )
A.(5x-2y)2 B.-(5x-2y)2
C.-(2y-5x)2 D.(5x)-(2y)2
4.若a-b=2 ，a-c=1，(2a-b-c)2+(c-a)2的值是( )
A.9 B.10 C.2 D.1
5. 已知(a+b)2=11, (a-b)2=7 ,则2ab为 ( )
A.2 B.-1 C.1 D.-2
（二）、利用公式进行计算：
(1)1232-124×122

(2) [(x+2y)2－(x＋y)(3x－y)－5ｙ2]÷（2x）其中，x=-2,y=
（3）(2a-b)2 (b+2a)2
板书
设计
第一章 乘法公式的应用
反思