北师大版数学七年级下册专题专练—微专题5 三角形内角和应用(含答案)
文档属性
| 名称 | 北师大版数学七年级下册专题专练—微专题5 三角形内角和应用(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 499.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 19:57:05 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
北师大版数学七年级下册专题专练
微专题5 三角形内角和应用
类型1 直接计算角度
1. 如图,在△ABC中,∠BAC=x,∠B=2x,∠C=3x,则∠BAD的度数为( )
A.145° B.150° C.155° D.160°
2. 在△ABC中,三个内角∠A,∠B,∠C满足∠B-∠A=∠C-∠B,则∠B= .
类型2 在三角板或直尺中计算
3. 已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为( )
A.20° B.30° C.45° D.50°
4. 如图,将一副三角板叠放在一起,使直角顶点重合于点O,AB∥OC,DC与OB交于点E,则∠DEO的度数为( )
A.85° B.70° C.75° D.60°
5. 已知直线a∥b,将一块含45°角的直角三角板(∠C=90°)按如图所示的位置摆放,若∠1=55°,则∠2的度数为( )
A.80° B.70° C.85° D.75°
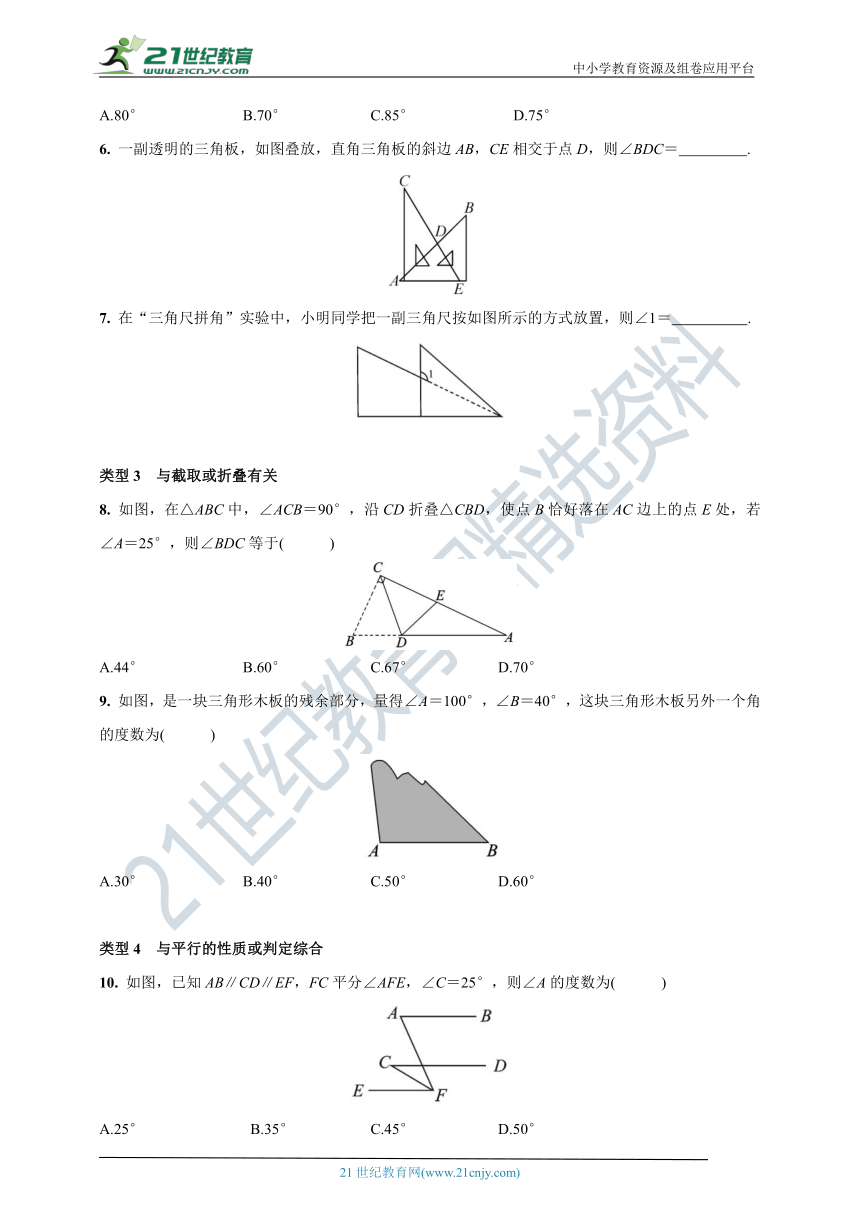
6. 一副透明的三角板,如图叠放,直角三角板的斜边AB,CE相交于点D,则∠BDC= .
7. 在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1= .
类型3 与截取或折叠有关
8. 如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC等于( )
A.44° B.60° C.67° D.70°
9. 如图,是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板另外一个角的度数为( )
A.30° B.40° C.50° D.60°
类型4 与平行的性质或判定综合
10. 如图,已知AB∥CD∥EF,FC平分∠AFE,∠C=25°,则∠A的度数为( )
A.25° B.35° C.45° D.50°
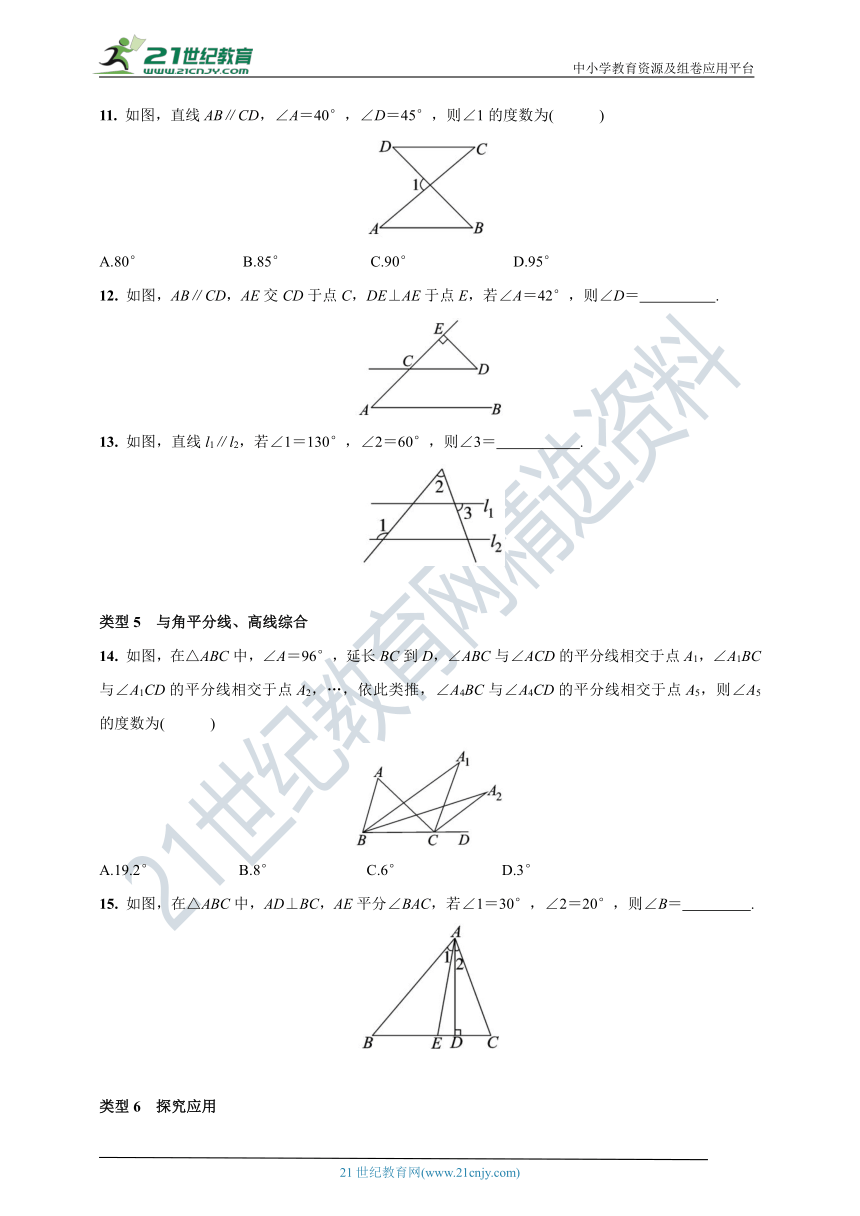
11. 如图,直线AB∥CD,∠A=40°,∠D=45°,则∠1的度数为( )
A.80° B.85° C.90° D.95°
12. 如图,AB∥CD,AE交CD于点C,DE⊥AE于点E,若∠A=42°,则∠D= .
13. 如图,直线l1∥l2,若∠1=130°,∠2=60°,则∠3= .
类型5 与角平分线、高线综合
14. 如图,在△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1,∠A1BC与∠A1CD的平分线相交于点A2,…,依此类推,∠A4BC与∠A4CD的平分线相交于点A5,则∠A5的度数为( )
A.19.2° B.8° C.6° D.3°
15. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B= .
类型6 探究应用
16. 如图1,在△ABC中,OB,OC分别是∠ABC,∠ACB的角平分线.
(1)填写下面的表格:
∠A的度数 50° 60° 70°
∠BOC的度数
(2)试猜想∠A与∠BOC之间存在一个怎样的数量关系,并证明你的猜想;
(3)如图2,△ABC的高BE,CD交于点O,试说明图中∠A与∠BOD的关系.
图1 图2
17. (1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY,XZ分别经过点B,C.在△ABC中,∠A=30°,则∠ABC+∠ACB= ,∠XBC+∠XCB= .
(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY,XZ仍然分别经过B,C,那么∠ABX+∠ACX的大小是否变化 若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
图1 图2
参 考 答 案
1. B
2. 60°
3. D 4. C 5. A
6. 75° 7. 120°
8. D 9. B 10. D 11. B
12. 48° 13. 70°
14. D
15. 50°
16. 解:(1)115° 120° 125°
(2)猜想:∠BOC=90°+∠A. 理由如下:∵在△ABC中,OB,OC是∠ABC,∠ACB的角平分线,∴∠OBC=∠ABC,∠OCB=∠ACB,∵∠ABC+∠ACB=180°-∠A,∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°-∠A)=90°-∠A,∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-∠A)=90°+∠A.
(3)∠A=∠BOD. 理由如下:∵△ABC的高BE,CD交于点O,∴∠BDC=∠BEA=90°,∴∠ABE+∠BOD=90°,∠ABE+∠A=90°,∴∠A=∠BOD.
17. 解:(1)150° 90°
(2)不变化. ∵∠A=30°,∴∠ABC+∠ACB=150°,又∵∠X=90°,∴∠XBC+∠XCB=90°,∴∠ABX+∠ACX=(∠ABC-∠XBC)+(∠ACB-∠XCB)=(∠ABC+∠ACB)-(∠XBC+∠XCB)=150°-90°=60°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师大版数学七年级下册专题专练
微专题5 三角形内角和应用
类型1 直接计算角度
1. 如图,在△ABC中,∠BAC=x,∠B=2x,∠C=3x,则∠BAD的度数为( )
A.145° B.150° C.155° D.160°
2. 在△ABC中,三个内角∠A,∠B,∠C满足∠B-∠A=∠C-∠B,则∠B= .
类型2 在三角板或直尺中计算
3. 已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上,若∠1=20°,则∠2的度数为( )
A.20° B.30° C.45° D.50°
4. 如图,将一副三角板叠放在一起,使直角顶点重合于点O,AB∥OC,DC与OB交于点E,则∠DEO的度数为( )
A.85° B.70° C.75° D.60°
5. 已知直线a∥b,将一块含45°角的直角三角板(∠C=90°)按如图所示的位置摆放,若∠1=55°,则∠2的度数为( )
A.80° B.70° C.85° D.75°
6. 一副透明的三角板,如图叠放,直角三角板的斜边AB,CE相交于点D,则∠BDC= .
7. 在“三角尺拼角”实验中,小明同学把一副三角尺按如图所示的方式放置,则∠1= .
类型3 与截取或折叠有关
8. 如图,在△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=25°,则∠BDC等于( )
A.44° B.60° C.67° D.70°
9. 如图,是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板另外一个角的度数为( )
A.30° B.40° C.50° D.60°
类型4 与平行的性质或判定综合
10. 如图,已知AB∥CD∥EF,FC平分∠AFE,∠C=25°,则∠A的度数为( )
A.25° B.35° C.45° D.50°
11. 如图,直线AB∥CD,∠A=40°,∠D=45°,则∠1的度数为( )
A.80° B.85° C.90° D.95°
12. 如图,AB∥CD,AE交CD于点C,DE⊥AE于点E,若∠A=42°,则∠D= .
13. 如图,直线l1∥l2,若∠1=130°,∠2=60°,则∠3= .
类型5 与角平分线、高线综合
14. 如图,在△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1,∠A1BC与∠A1CD的平分线相交于点A2,…,依此类推,∠A4BC与∠A4CD的平分线相交于点A5,则∠A5的度数为( )
A.19.2° B.8° C.6° D.3°
15. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B= .
类型6 探究应用
16. 如图1,在△ABC中,OB,OC分别是∠ABC,∠ACB的角平分线.
(1)填写下面的表格:
∠A的度数 50° 60° 70°
∠BOC的度数
(2)试猜想∠A与∠BOC之间存在一个怎样的数量关系,并证明你的猜想;
(3)如图2,△ABC的高BE,CD交于点O,试说明图中∠A与∠BOD的关系.
图1 图2
17. (1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY,XZ分别经过点B,C.在△ABC中,∠A=30°,则∠ABC+∠ACB= ,∠XBC+∠XCB= .
(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY,XZ仍然分别经过B,C,那么∠ABX+∠ACX的大小是否变化 若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
图1 图2
参 考 答 案
1. B
2. 60°
3. D 4. C 5. A
6. 75° 7. 120°
8. D 9. B 10. D 11. B
12. 48° 13. 70°
14. D
15. 50°
16. 解:(1)115° 120° 125°
(2)猜想:∠BOC=90°+∠A. 理由如下:∵在△ABC中,OB,OC是∠ABC,∠ACB的角平分线,∴∠OBC=∠ABC,∠OCB=∠ACB,∵∠ABC+∠ACB=180°-∠A,∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°-∠A)=90°-∠A,∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-∠A)=90°+∠A.
(3)∠A=∠BOD. 理由如下:∵△ABC的高BE,CD交于点O,∴∠BDC=∠BEA=90°,∴∠ABE+∠BOD=90°,∠ABE+∠A=90°,∴∠A=∠BOD.
17. 解:(1)150° 90°
(2)不变化. ∵∠A=30°,∴∠ABC+∠ACB=150°,又∵∠X=90°,∴∠XBC+∠XCB=90°,∴∠ABX+∠ACX=(∠ABC-∠XBC)+(∠ACB-∠XCB)=(∠ABC+∠ACB)-(∠XBC+∠XCB)=150°-90°=60°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
