冀教版数学四年级下册 9.1多边形的内角和课件(共18张PPT)
文档属性
| 名称 | 冀教版数学四年级下册 9.1多边形的内角和课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 334.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-02 16:04:24 | ||
图片预览



文档简介
(共18张PPT)
九 探索乐园
9.1 多边形的内角和
学习目标
1.了解多边形及多边形的内角概念。
2.通过不同方法探索多边形的内角和公式,并会利用它进行有关计算。
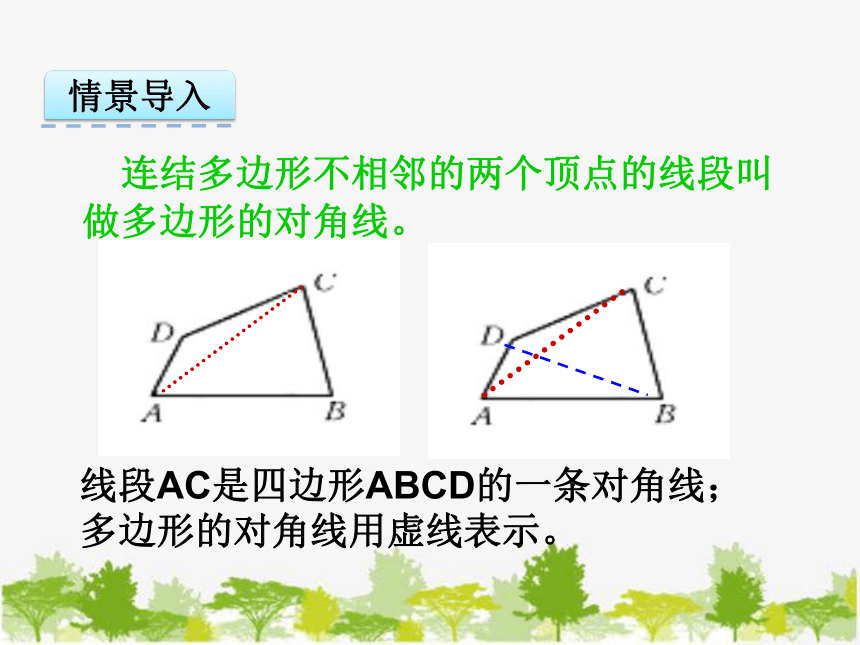
连结多边形不相邻的两个顶点的线段叫做多边形的对角线。
线段AC是四边形ABCD的一条对角线;
多边形的对角线用虚线表示。
情景导入
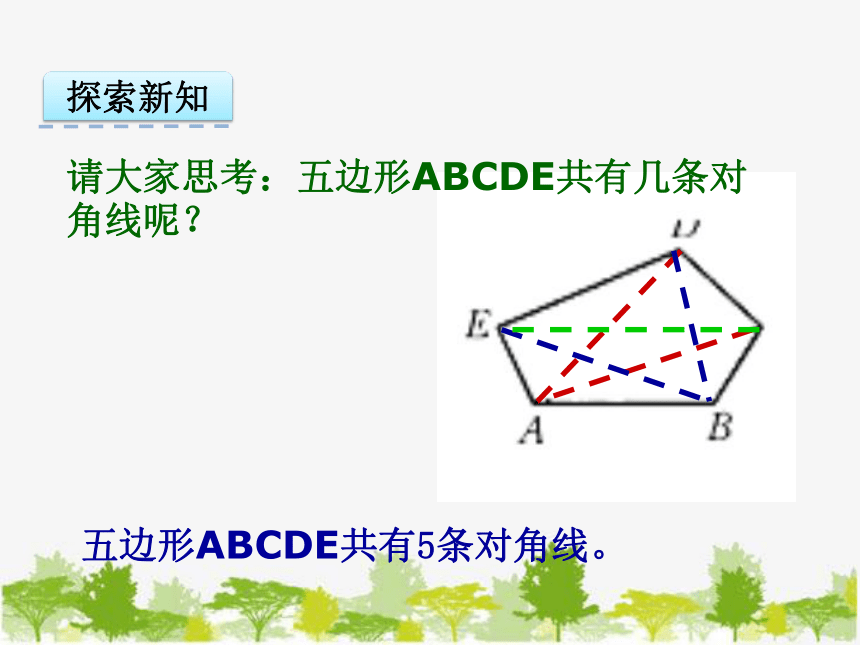
请大家思考:五边形ABCDE共有几条对角线呢?
五边形ABCDE共有5条对角线。
探索新知
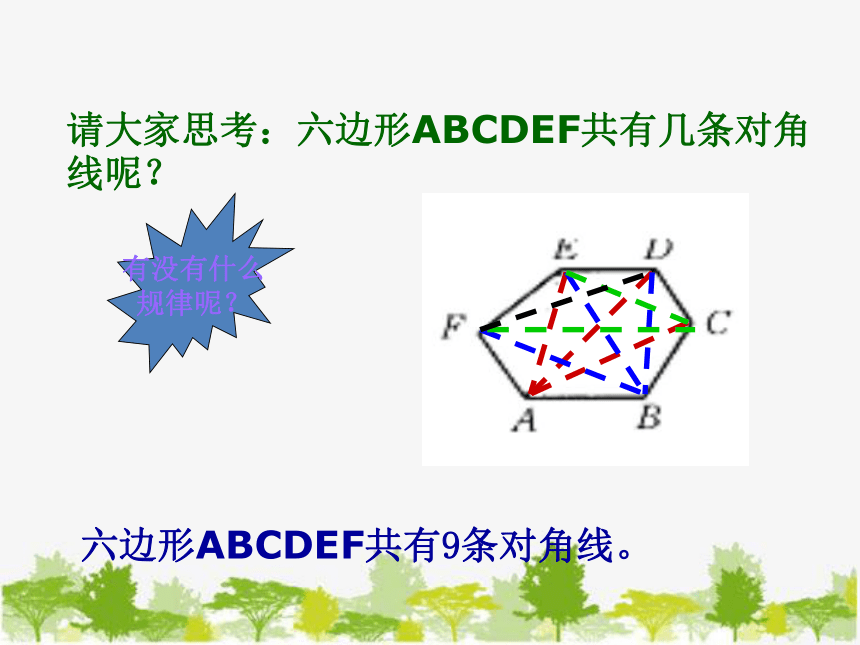
请大家思考:六边形ABCDEF共有几条对角线呢?
六边形ABCDEF共有9条对角线。
有没有什么
规律呢?
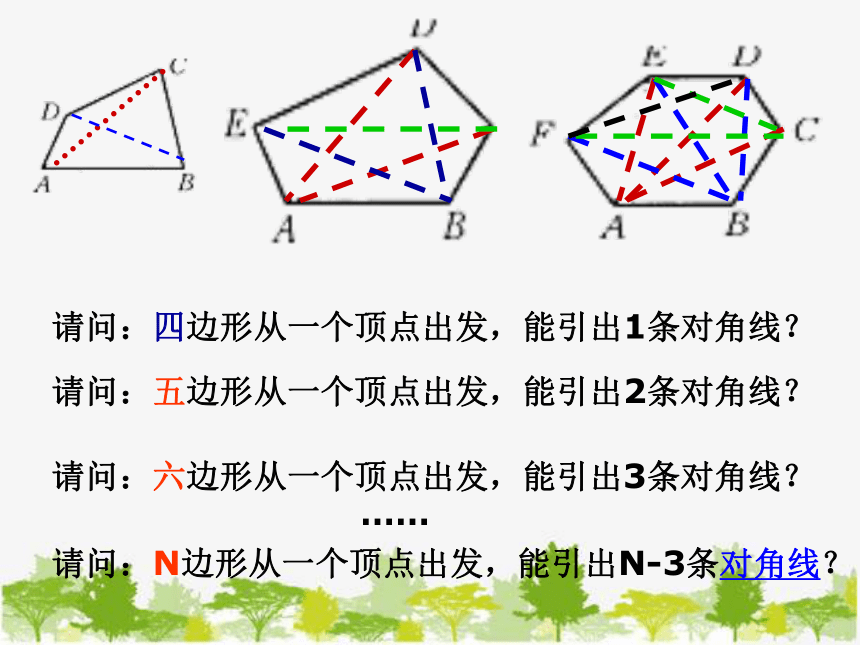
请问:四边形从一个顶点出发,能引出几条对角线?
请问:五边形从一个顶点出发,能引出几条对角线?
请问:六边形从一个顶点出发,能引出几条对角线?
请问:N边形从一个顶点出发,能引出几条对角线?
……
请问:四边形从一个顶点出发,能引出1条对角线?
请问:五边形从一个顶点出发,能引出2条对角线?
请问:六边形从一个顶点出发,能引出3条对角线?
请问:N边形从一个顶点出发,能引出N-3条对角线?
……
我们已经知道一个三角形的内角和等于180°,那么四边形的内角和等于多少呢?五边形、六边形呢?由此,n边形的内角和等于多少呢?
我们学习数学的
基本思想什么?
化未知为已知
那么我们能不能利用三角形的内角和,来求出四边形的内角和,以及五边形、六边形,n边形的内角和?
请你认真地想一想,你能通过怎样的方法把多边形转化为三角形?
3
4
5
n-2
540 °
720 °
900 °
180 ° (n-2)
1.从一个顶点出发的对角线有(n-3)条
探索多边形的内角和
由此,我们就可以得出 :
n边形的内角和为_________________.
(n-2) 180 °
它有什么作用呢
1.知道多边形的边数,可以求出多边形的度数.
2.知道多边形的度数,可以求出多边形的边数.
求八边形的内角和的度数.
解 (n-2)×180°
=(8-2)×180°
=1 080°
分析: n边形的内角和公式为(n-2) 180 °,现在知道这个多边形的边数,代入这个公式既可求出.
典题精讲
已知多边形的内角和的度数为900°,则这个多边形的边数为________
解 (n-2)×180° = 900°
(n-2)= 900° /180°
(n-2) = 5
n= 5 +2
n=7
7
学以致用
已知在一个十边形中,九个内角的和的度数是1290°,求这个十边形的另一个内角的度数.
解: (10-2)×180° =1440 °
则十边形的另一个内角的度数为
1440 °- 1290° =150 °
先求出十边形的内角和再减去1290°,就可以得出.
那么对于正多边形来说,又遇到怎样的问题呢
因为正多边形的每个角相等,所以知道
正多边形的边数,就可以求出每一个内角的度数.
(n-2)×180°/ n
正五边形的每一个内角等于_____,外角等于___.
解: (n-2)×180°/ n
= (5-2)×180°/5
=540°/5
=108°
如果一个正多边形的一个内角等于120°,则这个多边形的边数是_____
解: 120°n=(n-2)×180°
120°n=n×180°-360 °
60°n =360 °
n =6
如果一个正多边形的一个内角等于150°,则这个多边形的边数是_____
A.12 B.9 C. 8 D.7
A
如果一个多边形的边数增加1,则这个多边形的内角和_____
增加180 °
如果一个多边形的每一个外角等于30°,则这个多边形的边数是____
12
课堂小结
今天你都收获了什么?
九 探索乐园
9.1 多边形的内角和
学习目标
1.了解多边形及多边形的内角概念。
2.通过不同方法探索多边形的内角和公式,并会利用它进行有关计算。
连结多边形不相邻的两个顶点的线段叫做多边形的对角线。
线段AC是四边形ABCD的一条对角线;
多边形的对角线用虚线表示。
情景导入
请大家思考:五边形ABCDE共有几条对角线呢?
五边形ABCDE共有5条对角线。
探索新知
请大家思考:六边形ABCDEF共有几条对角线呢?
六边形ABCDEF共有9条对角线。
有没有什么
规律呢?
请问:四边形从一个顶点出发,能引出几条对角线?
请问:五边形从一个顶点出发,能引出几条对角线?
请问:六边形从一个顶点出发,能引出几条对角线?
请问:N边形从一个顶点出发,能引出几条对角线?
……
请问:四边形从一个顶点出发,能引出1条对角线?
请问:五边形从一个顶点出发,能引出2条对角线?
请问:六边形从一个顶点出发,能引出3条对角线?
请问:N边形从一个顶点出发,能引出N-3条对角线?
……
我们已经知道一个三角形的内角和等于180°,那么四边形的内角和等于多少呢?五边形、六边形呢?由此,n边形的内角和等于多少呢?
我们学习数学的
基本思想什么?
化未知为已知
那么我们能不能利用三角形的内角和,来求出四边形的内角和,以及五边形、六边形,n边形的内角和?
请你认真地想一想,你能通过怎样的方法把多边形转化为三角形?
3
4
5
n-2
540 °
720 °
900 °
180 ° (n-2)
1.从一个顶点出发的对角线有(n-3)条
探索多边形的内角和
由此,我们就可以得出 :
n边形的内角和为_________________.
(n-2) 180 °
它有什么作用呢
1.知道多边形的边数,可以求出多边形的度数.
2.知道多边形的度数,可以求出多边形的边数.
求八边形的内角和的度数.
解 (n-2)×180°
=(8-2)×180°
=1 080°
分析: n边形的内角和公式为(n-2) 180 °,现在知道这个多边形的边数,代入这个公式既可求出.
典题精讲
已知多边形的内角和的度数为900°,则这个多边形的边数为________
解 (n-2)×180° = 900°
(n-2)= 900° /180°
(n-2) = 5
n= 5 +2
n=7
7
学以致用
已知在一个十边形中,九个内角的和的度数是1290°,求这个十边形的另一个内角的度数.
解: (10-2)×180° =1440 °
则十边形的另一个内角的度数为
1440 °- 1290° =150 °
先求出十边形的内角和再减去1290°,就可以得出.
那么对于正多边形来说,又遇到怎样的问题呢
因为正多边形的每个角相等,所以知道
正多边形的边数,就可以求出每一个内角的度数.
(n-2)×180°/ n
正五边形的每一个内角等于_____,外角等于___.
解: (n-2)×180°/ n
= (5-2)×180°/5
=540°/5
=108°
如果一个正多边形的一个内角等于120°,则这个多边形的边数是_____
解: 120°n=(n-2)×180°
120°n=n×180°-360 °
60°n =360 °
n =6
如果一个正多边形的一个内角等于150°,则这个多边形的边数是_____
A.12 B.9 C. 8 D.7
A
如果一个多边形的边数增加1,则这个多边形的内角和_____
增加180 °
如果一个多边形的每一个外角等于30°,则这个多边形的边数是____
12
课堂小结
今天你都收获了什么?
