山东省聊城市某重点中学2013届高三下学期期初考试数学文试题
文档属性
| 名称 | 山东省聊城市某重点中学2013届高三下学期期初考试数学文试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 355.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-19 00:00:00 | ||
图片预览


文档简介
山东省聊城市某重点中学2013届高三下学期期初考试文科数学试题
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷
一、选择题
1.已知三个平面,若,且相交但不垂直,分别为内的直线,则( )21世纪教育网
A. B. C. D.
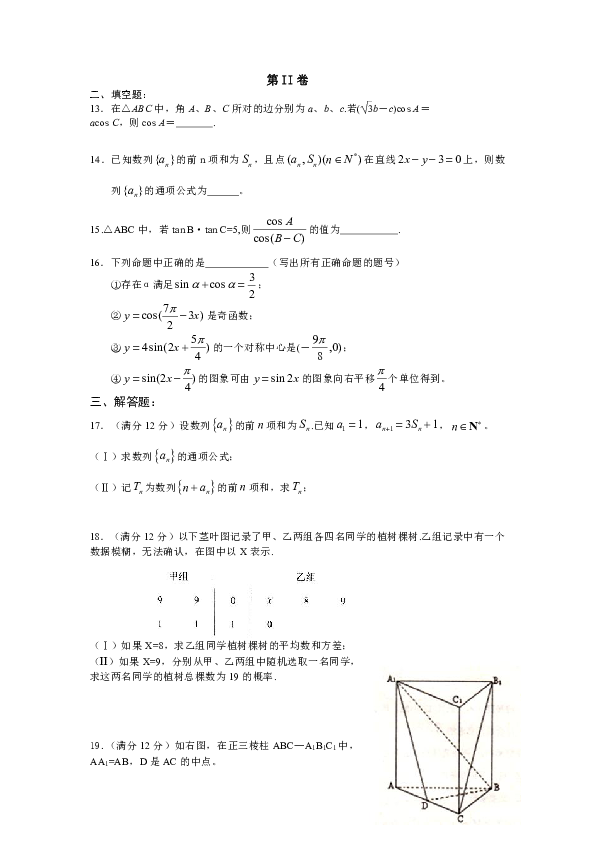
2.已知是实数,则函数的图像可能是 ( )
A. B. C. D.
3.若且2=2,则的最小值是( )
A.2 B. C. D.
4.已知函数的定义域为R,当时,,且对任意的实数R,等式成立.若数列满足,且
(N*),则的值为( )
A. 4024 B.4023 C.4022 D.4021
5.定义函数,若存在常数C,对任意的,存在唯一的,使得,则称函数在D上的几何平均数为C.已知,则函数在上的几何平均数为( )
A. B. C. D.21世纪教育网
6.已知则成立的( )
(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分也不必要条件
7. 已知向量,,且与的夹角为锐角,则的取值范围是( )
(A) (B) (C) (D)
8. 已知函数(其中)的
部分图象如右图所示,为了得到的图象,则只需将的图象( )
(A)向右平移个长度单位 (B)向右平移个长度单位
(C)向左平移个长度单位 (D)向左平移个长度单位
9.曲线上切点为的切线方程是( )
(A) (B) (C) (D)或
10. 下列命题:①在中,若,则;②已知,则在上的投影为;③已知,,则“”为假命题.其中真命题的个数为( )
(A)0 (B)1 (C)2 (D)3
11. 设圆锥曲线的两个焦点分别为、,若曲线上存在点满足::=4:3:2,则曲线的离心率等于( )
(A) (B) (C) (D)
12.对于三次函数(),定义:设f″(x)是函数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数的“拐点”.有同学发现:“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现为条件,若函数,则
=( )
(A)2010 (B)2011 (C)2012 (D)2013
第II卷
二、填空题:
13.在△ABC中,角A、B、C所对的边分别为a、b、c.若(b-c)cos A=
acos C,则cos A= .
14.已知数列的前n项和为,且点在直线上,则数列的通项公式为 。
15.△ABC中,若tan B·tan C=5,则的值为 .
16.下列命题中正确的是 (写出所有正确命题的题号)
①存在α满足;
②是奇函数;
③的一个对称中心是(-;
④的图象可由的图象向右平移个单位得到。
三、解答题:
17.(满分12分)设数列的前项和为.已知,,。
(Ⅰ)求数列的通项公式;
(Ⅱ)记为数列的前项和,求;
18.(满分12分)以下茎叶图记录了甲、乙两组各四名同学的植树棵树.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
(Ⅰ)如果X=8,求乙组同学植树棵树的平均数和方差;
(II)如果X=9,分别从甲、乙两组中随机选取一名同学,
求这两名同学的植树总棵数为19的概率.
19.(满分12分)如右图,在正三棱柱ABC—A1B1C1中,AA1=AB,D是AC的中点。
(Ⅰ)求证:B1C//平面A1BD;
(Ⅰ)求二面角A—A1B—D的余弦值。
20.(满分12分)已知椭圆的一个顶点为B,离心率,
直线l交椭圆于M、N两点.
(Ⅰ)求椭圆的标准方程;
(II)如果ΔBMN的重心恰好为椭圆的右焦点F,求直线的方程.
21.(满分12分)设函数.
(Ⅰ)求函数的单调递增区间;
(II)若关于的方程在区间内恰有两个相异的实根,求实数的取值范围.
22.(满分10分)
如下图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(I)求AC的长;
(II)求证:BE=EF.
高二数学(文)答案
1-5ACDBC 6~10 A BAAC 11~12 DA
13. ;14. ;15. ;16.②③
17.(满分12分)
解:(Ⅰ)由题意,,则当时,.
两式相减,得(). ……………………………………………2分
又因为,,,………………………21世纪教育网……………4分
所以数列是以首项为,公比为的等比数列,……………………5分
所以数列的通项公式是(). ………………………………6分
(Ⅱ)因为,
………………………………12分
18.(满分12分)
解:(1)当X=8时,由茎叶图可知,乙组同学的植树棵数是:8,8,9,10,
所以平均数为……………………………………3分
方差为………………………6分
(Ⅱ)记甲组四名同学为A1,A2,A3,A4,他们植树的棵数依次为9,9,11,11;乙组四名同学为B1,B2,B3,B4,他们植树的棵数依次为9,8,9,10,分别从甲、乙两组中随机选取一名同学,所有可能的结果有16个,它们是:
(A1,B1),(A1,B2),(A1,B3),(A1,B4),
(A2,B1),(A2,B2),(A2,B3),(A2,B4),
(A3,B1),(A2,B2),(A3,B3),(A1,B4),
(A4,B1),(A4,B2),(A4,B3),(A4,B4),
用C表示:“选出的两名同学的植树总棵数为19”这一事件,则C中的结果有4个,它们是:(A1,B4),(A2,B4),(A3,B2),(A4,B2),故所求概率为……12分
19.(满分12分)
解:(1)证明:连交于点,连.
则是的中点,
∵是的中点,∴
∵平面,平面,∴∥平面.…………………6分
(2)法一:设,∵,∴,且,
作,连
∵平面⊥平面,∴平面,
∴∴就是二面角的平面角,
在中,,
在中,
,即二面角的余弦值是.…………12分
解法二:如图,建立空间直角坐标系.
则,,,.
∴,,,
设平面的法向量是,则
由,取
设平面的法向量是,则
由,取
记二面角的大小是,则,
即二面角的余弦值是.…………………………12分
20.(满分12分)
解:(1)由已知,且,即,
∴,解得,∴椭圆的方程标准为; …21世纪教育网…………5分
(2)椭圆右焦点F的坐标为,
设线段MN的中点为Q,
由三角形重心的性质知,又,
∴,故得,
求得Q的坐标为; ……………………8分
设,则,
且, ……………………10分
以上两式相减得,
,
故直线MN的方程为,即. ……………………12分
21.(满分12分)
(1)函数的定义域为,………………………………………………1分
∵, ………………………………………2分
∵,则使的的取值范围为,
故函数的单调递增区间为. ……………………………………………4分
(2)方法1:∵,
∴. …………………………6分
令,
∵,且,
由.
∴在区间内单调递减,在区间内单调递增, ……………………8分
故在区间内恰有两个相异实根 ……10分
即解得:.
综上所述,的取值范围是. 21世纪教育网…………………………12分
方法2:∵,
∴. …………………………6分
即,
令, ∵,且,
由.
∴在区间内单调递增,在区间内单调递减.……………………8分
∵,,,
又,
故在区间内恰有两个相异实根.
……………………………………10分
即.
综上所述,的取值范围是. ………………21世纪教育网……12分
22.(满分10分)
解:(I),,…(2分)
又,
,,…………(4分)
, …………(5分)
(II),,而, …………(8分)
,. …21世纪教育网…(10分)
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷
一、选择题
1.已知三个平面,若,且相交但不垂直,分别为内的直线,则( )21世纪教育网
A. B. C. D.
2.已知是实数,则函数的图像可能是 ( )
A. B. C. D.
3.若且2=2,则的最小值是( )
A.2 B. C. D.
4.已知函数的定义域为R,当时,,且对任意的实数R,等式成立.若数列满足,且
(N*),则的值为( )
A. 4024 B.4023 C.4022 D.4021
5.定义函数,若存在常数C,对任意的,存在唯一的,使得,则称函数在D上的几何平均数为C.已知,则函数在上的几何平均数为( )
A. B. C. D.21世纪教育网
6.已知则成立的( )
(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分也不必要条件
7. 已知向量,,且与的夹角为锐角,则的取值范围是( )
(A) (B) (C) (D)
8. 已知函数(其中)的
部分图象如右图所示,为了得到的图象,则只需将的图象( )
(A)向右平移个长度单位 (B)向右平移个长度单位
(C)向左平移个长度单位 (D)向左平移个长度单位
9.曲线上切点为的切线方程是( )
(A) (B) (C) (D)或
10. 下列命题:①在中,若,则;②已知,则在上的投影为;③已知,,则“”为假命题.其中真命题的个数为( )
(A)0 (B)1 (C)2 (D)3
11. 设圆锥曲线的两个焦点分别为、,若曲线上存在点满足::=4:3:2,则曲线的离心率等于( )
(A) (B) (C) (D)
12.对于三次函数(),定义:设f″(x)是函数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数的“拐点”.有同学发现:“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现为条件,若函数,则
=( )
(A)2010 (B)2011 (C)2012 (D)2013
第II卷
二、填空题:
13.在△ABC中,角A、B、C所对的边分别为a、b、c.若(b-c)cos A=
acos C,则cos A= .
14.已知数列的前n项和为,且点在直线上,则数列的通项公式为 。
15.△ABC中,若tan B·tan C=5,则的值为 .
16.下列命题中正确的是 (写出所有正确命题的题号)
①存在α满足;
②是奇函数;
③的一个对称中心是(-;
④的图象可由的图象向右平移个单位得到。
三、解答题:
17.(满分12分)设数列的前项和为.已知,,。
(Ⅰ)求数列的通项公式;
(Ⅱ)记为数列的前项和,求;
18.(满分12分)以下茎叶图记录了甲、乙两组各四名同学的植树棵树.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
(Ⅰ)如果X=8,求乙组同学植树棵树的平均数和方差;
(II)如果X=9,分别从甲、乙两组中随机选取一名同学,
求这两名同学的植树总棵数为19的概率.
19.(满分12分)如右图,在正三棱柱ABC—A1B1C1中,AA1=AB,D是AC的中点。
(Ⅰ)求证:B1C//平面A1BD;
(Ⅰ)求二面角A—A1B—D的余弦值。
20.(满分12分)已知椭圆的一个顶点为B,离心率,
直线l交椭圆于M、N两点.
(Ⅰ)求椭圆的标准方程;
(II)如果ΔBMN的重心恰好为椭圆的右焦点F,求直线的方程.
21.(满分12分)设函数.
(Ⅰ)求函数的单调递增区间;
(II)若关于的方程在区间内恰有两个相异的实根,求实数的取值范围.
22.(满分10分)
如下图,AB、CD是圆的两条平行弦,BE//AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.
(I)求AC的长;
(II)求证:BE=EF.
高二数学(文)答案
1-5ACDBC 6~10 A BAAC 11~12 DA
13. ;14. ;15. ;16.②③
17.(满分12分)
解:(Ⅰ)由题意,,则当时,.
两式相减,得(). ……………………………………………2分
又因为,,,………………………21世纪教育网……………4分
所以数列是以首项为,公比为的等比数列,……………………5分
所以数列的通项公式是(). ………………………………6分
(Ⅱ)因为,
………………………………12分
18.(满分12分)
解:(1)当X=8时,由茎叶图可知,乙组同学的植树棵数是:8,8,9,10,
所以平均数为……………………………………3分
方差为………………………6分
(Ⅱ)记甲组四名同学为A1,A2,A3,A4,他们植树的棵数依次为9,9,11,11;乙组四名同学为B1,B2,B3,B4,他们植树的棵数依次为9,8,9,10,分别从甲、乙两组中随机选取一名同学,所有可能的结果有16个,它们是:
(A1,B1),(A1,B2),(A1,B3),(A1,B4),
(A2,B1),(A2,B2),(A2,B3),(A2,B4),
(A3,B1),(A2,B2),(A3,B3),(A1,B4),
(A4,B1),(A4,B2),(A4,B3),(A4,B4),
用C表示:“选出的两名同学的植树总棵数为19”这一事件,则C中的结果有4个,它们是:(A1,B4),(A2,B4),(A3,B2),(A4,B2),故所求概率为……12分
19.(满分12分)
解:(1)证明:连交于点,连.
则是的中点,
∵是的中点,∴
∵平面,平面,∴∥平面.…………………6分
(2)法一:设,∵,∴,且,
作,连
∵平面⊥平面,∴平面,
∴∴就是二面角的平面角,
在中,,
在中,
,即二面角的余弦值是.…………12分
解法二:如图,建立空间直角坐标系.
则,,,.
∴,,,
设平面的法向量是,则
由,取
设平面的法向量是,则
由,取
记二面角的大小是,则,
即二面角的余弦值是.…………………………12分
20.(满分12分)
解:(1)由已知,且,即,
∴,解得,∴椭圆的方程标准为; …21世纪教育网…………5分
(2)椭圆右焦点F的坐标为,
设线段MN的中点为Q,
由三角形重心的性质知,又,
∴,故得,
求得Q的坐标为; ……………………8分
设,则,
且, ……………………10分
以上两式相减得,
,
故直线MN的方程为,即. ……………………12分
21.(满分12分)
(1)函数的定义域为,………………………………………………1分
∵, ………………………………………2分
∵,则使的的取值范围为,
故函数的单调递增区间为. ……………………………………………4分
(2)方法1:∵,
∴. …………………………6分
令,
∵,且,
由.
∴在区间内单调递减,在区间内单调递增, ……………………8分
故在区间内恰有两个相异实根 ……10分
即解得:.
综上所述,的取值范围是. 21世纪教育网…………………………12分
方法2:∵,
∴. …………………………6分
即,
令, ∵,且,
由.
∴在区间内单调递增,在区间内单调递减.……………………8分
∵,,,
又,
故在区间内恰有两个相异实根.
……………………………………10分
即.
综上所述,的取值范围是. ………………21世纪教育网……12分
22.(满分10分)
解:(I),,…(2分)
又,
,,…………(4分)
, …………(5分)
(II),,而, …………(8分)
,. …21世纪教育网…(10分)
同课章节目录
