山东省聊城市某重点中学2013届高三下学期期初考试数学理试题
文档属性
| 名称 | 山东省聊城市某重点中学2013届高三下学期期初考试数学理试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 222.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-19 00:00:00 | ||
图片预览




文档简介
山东省聊城市某重点中学2013届高三下学期期初考试理科数学试题
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷
一、选择题
1.已知圆,圆,其中,则两圆的位置关系为( )
A.相交 B.外切 C.内切 D.相交或外切
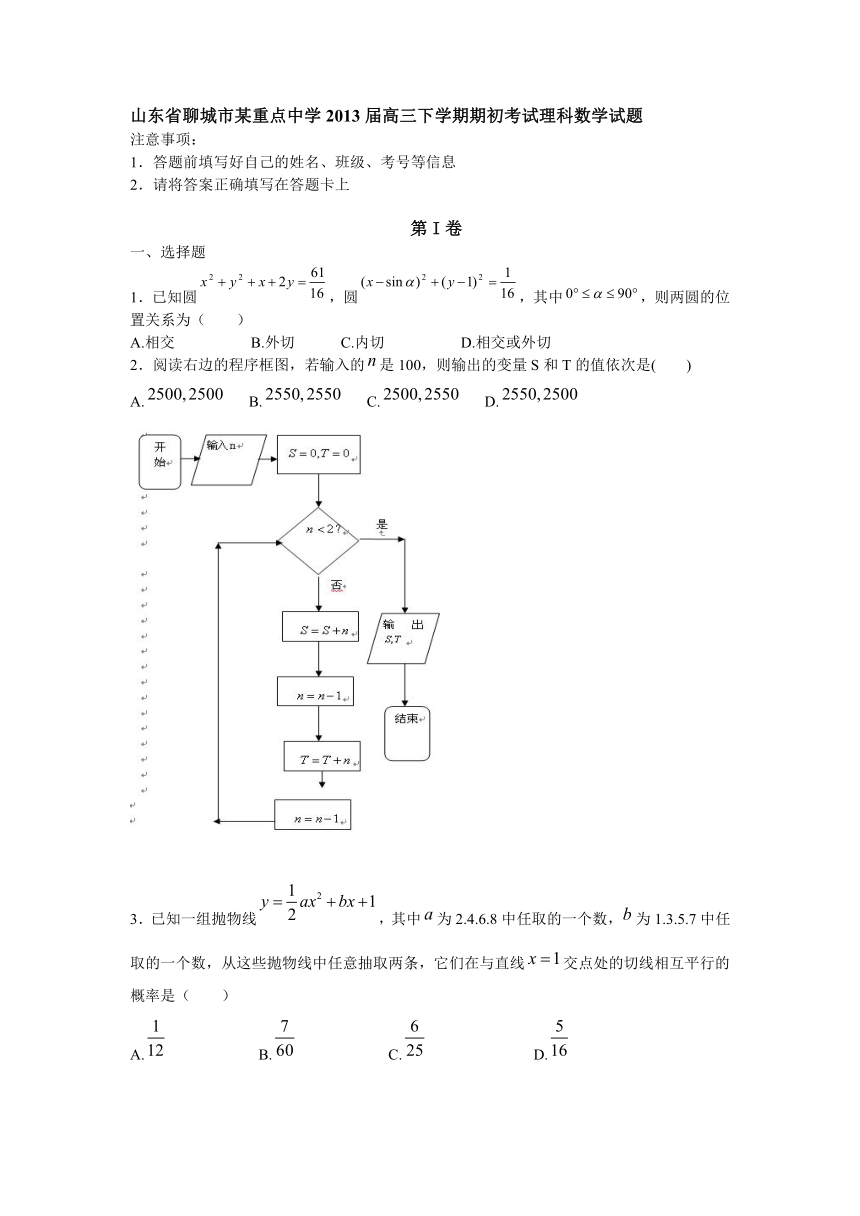
2.阅读右边的程序框图,若输入的是100,则输出的变量S和T的值依次是( )
A. B. C. D.
3.已知一组抛物线,其中为2.4.6.8中任取的一个数,为1.3.5.7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线交点处的切线相互平行的概率是( )
A. B. C. D.
4.设e1,e2分别为具有公共焦点F1与F2的椭圆和双曲线的离心率,P为两曲线的一个公共点,且满足·=0,则的值为( )
A. B.1 C.2 D.不确定
5.把函数y=cos(x+)的图象向右平移φ个单位,所得到的图象正好是关于y轴对称,则φ的最小正值是 ( )
A. B. C. D.
6.如图,体积为V的大球内有4个小球,每个小球的球面过大球球心且与大球球面有且只有一个交点,4个小球的球心是以大球球心为中心的正方形的4个顶点.V1为小球相交部分(图中阴影部分)的体积,V2为大球内、小球外的图中黑色部分的体积,则下列关系中正确的是( )
A. B.
C. D.
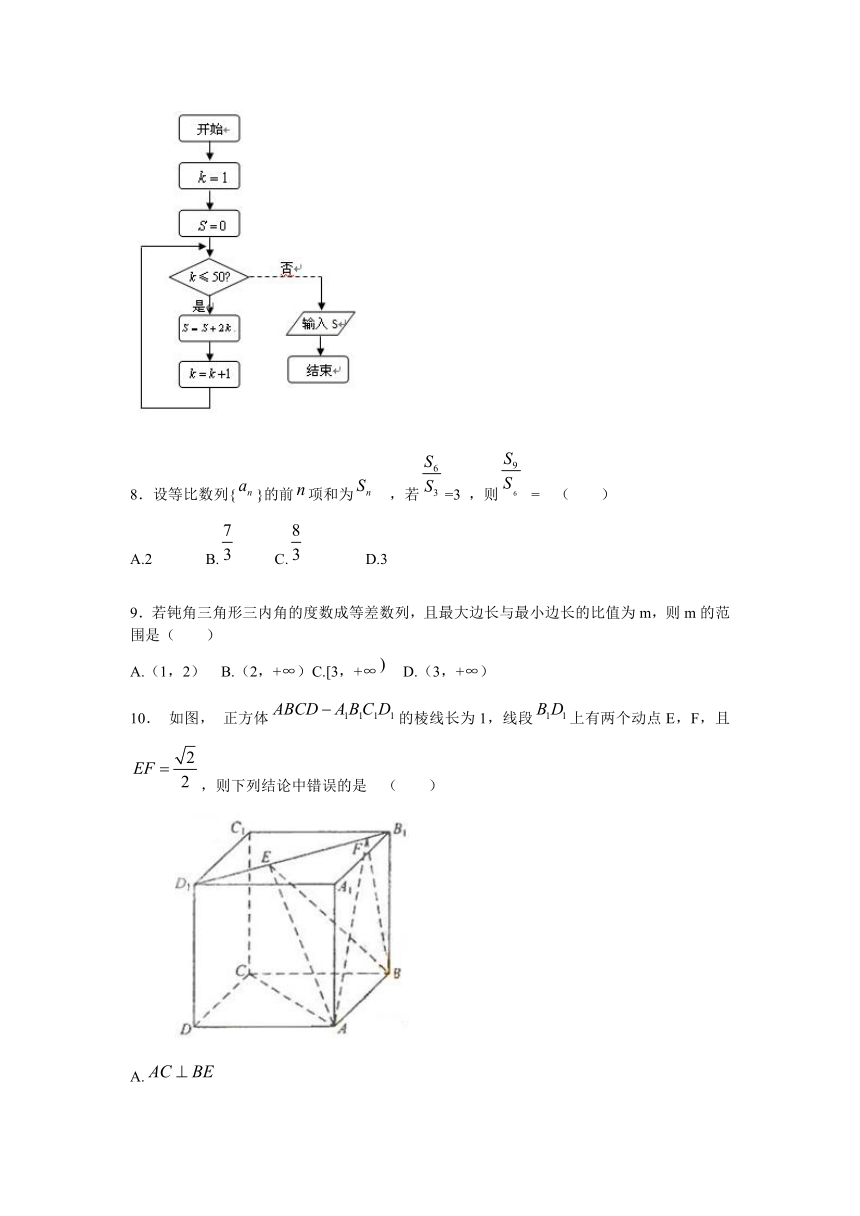
7.如果执行右面的程序框图,那么输出的( )
A.2450 B.2500 21世纪教育网
C.2550 D.2652
8.设等比数列{}的前项和为 ,若=3 ,则 = ( )
A.2 B. C. D.3
9.若钝角三角形三内角的度数成等差数列,且最大边长与最小边长的比值为m,则m的范围是( )
A.(1,2) B.(2,+∞) C.[3,+∞ D.(3,+∞)
10. 如图, 正方体的棱线长为1,线段上有两个动点E,F,且,则下列结论中错误的是 ( )
A.
B.
C.三棱锥的体积为定值
D.异面直线所成的角为定值
第II卷
二、填空题
11.若为非零实数,则下列四个命题都成立:
① ② ③若,则
④若,则。则对于任意非零复数,上述命题仍然成立的序号是 。
12.设等差数列的前项和为,若,则的最大值为___________。
13.已知数列满足则的最小值为__________.
14.若关于x的不等式ax2一|x|+2a0的解集为,则实数。的取值范围为_________.
三、解答题(本大题共6小题,共0分)
15.如图,A1A是圆柱的母线,AB是圆柱底面圆的直径,C是底面圆周上异于A,B的任意一点,AA1=AB=2.
(1)求证:BC上平面A1AC; ︿
(2)求三棱锥A1一ABC的体积的最大值
16.已知函数,常数.
(1)当时,解不等式;
(2)讨论函数的奇偶性,并说明理由
17.
已知数列中, .
(Ⅰ)设,求数列的通项公式;
(Ⅱ)求使不等式成立的的取值范围.
18.设函数
(I)研究函数的单调性;
(II)比较与0的大小,并证明你的结论;
(III)判断关于x的方程的实数解的个数,并加以证明。
19.已知,点在函数的图象上,其中
⑴证明数列是等比数列;
⑵设,求及数列的通项;
⑶记,求数列的前项,并证明
20.已知梯形ABCD中,AD∥BC,∠ABC =∠BAD =,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
(1) 当x=2时,求证:BD⊥EG ;
(2) 若以F、B、C、D为顶点的三棱锥的体积记为f(x),求f(x)的最大值;
(3) 当 f(x)取得最大值时,求二面角D-BF-C的余弦值.
高二数学(理)答案
一、选择题
1.D??????2.D??????
解析:依据框图可得,
3.B??????
解析:这一组抛物线共条,从中任意抽取两条,共有种不同的方法.它们在与直线交点处的切线的斜率.若,有两种情形,从中取出两条,有种取法;若,有三种情形,从中取出两条,有种取法;若,有四种情形,从中取出两条,有种取法;若,有三种情形,从中取出两条,有种取法;若,有两种情形,从中取出两条,有种取法.由分类计数原理知任取两条切线平行的情形共有种,故所求概率为.本题是把关题.
4.C??????
解析:设a1 为椭圆的长半轴长,a2 为双曲线的实半轴长,当P点在双曲线的右支上时,由题意得,, |PF1 |=+,|PF2 |=-,由·=0,得 即PF1 PF2 , (+)2 +(一)2=4c2 ,? 22 +22 =4c2 , ? +=2,从而==+=2, ? 当P点在双曲线盯左支上时,解法同上,故选C
5.B??????6.D??????
解析:设大球半径为 ,小球半径为 根据题意所以 于是即所以,
7.C??????
解析:
8.B??????
解析:因为数列是等比数列,所以,,有,即,故.
9.B??????10.D??????
解析:A正确,易证B显然正确,;C正确,可用等积法求得;D错误。选D.
二、填空题
11.②④
12.4
13.
14.[,+∞)
三、解答题
15.解:(1) C是底面圆周上异于A、B的一点,且AB为底面圆的直径, ??? BCAC ??? AA1 平面ABC,BC平面ABC, ??? AA1 BC ??? AA1 AC=A,AA1 平面A1 AC,AC平面A1 AC, ??? BC平面A1 AC ? (2)解法一设AC=x,在Rt△ABC中,BC== (0x2), 故VA -ABC = S△ABC ·AA1 =××AC×BC × A A1 =x(0x2), 即VA -ABC =x== 0x2.0x2 4. ? 当x2 =2,即x=时,三棱锥A1 -ABC的体积取到最大值 解法二在Rt△ABC中,AC2 +BC2 =AB2 =4,VA -ABC = S△ABC ·AA1 =××AC×BC×A A1 =×AC×BC×=×= 当且仅当AC=BC时等号成立,此时AC=BC=:三棱锥A1 -ABC的体积的最大值为
16.解: (1), ????????????? ,????????????????? ????????????? .??????????????? ???? 原不等式的解为.????????? ??? (2)当时,, ??? 对任意,, ??? 为偶函数.? ??? 当时,, ??? 取,得 , ??? ,??? 函数既不是奇函数,也不是偶函数.
17.解: (Ⅰ), 所以是首项为,公比为4的等比数列, (Ⅱ) 用数学归纳法证明:当时. (ⅰ)当时,,命题成立; (ⅱ)设当n=k时,,则当n=k+1时, 故由(ⅰ)(ⅱ)知,当c>2时 当c>2时,令,由得 当 当时,,且 于是 当时, 因此不符合要求 所以c的取值范围是
18.解(I) 所以单调递减。 ?? (II)(解法1): ?? (解法2): ?? (III) ①当 ②当 综合单调递减。
19.(Ⅰ)由已知, ??? ,两边取对数得 ,即 是公比为2的等比数列. (Ⅱ)由(Ⅰ)知????????????? ?????????????????? (*) = 由(*)式得 (Ⅲ),, 又, ,??? 又???? .
20. 解:(1)(法一)∵平面平面,AE⊥EF,∴AE⊥面,AE⊥EF,AE⊥BE,又BE⊥EF,故可如图建立空间坐标系E-xyz。 则A(0,0,2),B(2,0,0),G(2,2,0),D(0,2,2),E(0,0,0) (-2,2,2),(2,2,0) (-2,2,2)·(2,2,0)=0,∴ (法二)作DH⊥EF于H,连BH,GH, 由平面平面知:DH⊥平面EBCF, 而EG平面EBCF,故EG⊥DH。 又四边形BGHE为正方形,∴EG⊥BH, BHDH=H,故EG⊥平面DBH, 而BD平面DBH,∴ EG⊥BD。 (或者直接利用三垂线定理得出结果) (2)∵AD∥面BFC, 所以 VA-BFC ==··4·(4-x)·x 即时有最大值为。 (3)(法一)设平面DBF的法向量为, ∵AE=2, B(2,0,0),D(0,2,2), F(0,3,0),∴(-2,2,2), 则 , 即, 取x=3,则y=2,z=1,∴? 面BCF的一个法向量为 则cos<>= 由于所求二面角D-BF-C的平面角为钝角, 所以此二面角的余弦值为-?? (法二)作DH⊥EF于H,作HM⊥BF,连DM。 由三垂线定理知 BF⊥DM,∴∠DMH是二面角D-BF-C的平面角的补角。 由△HMF∽△EBF,知,而HF=1,BE=2,, ∴HM=。? 又DH=2, ∴在Rt△HMD中,tan∠DMH=-,21世纪教育网 因∠DMH为锐角,∴cos∠DMH=, 而∠DMH是二面角D-BF-C的平面角的补角, 故二面角D-BF-C的余弦值为-。21世纪教育网
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷
一、选择题
1.已知圆,圆,其中,则两圆的位置关系为( )
A.相交 B.外切 C.内切 D.相交或外切
2.阅读右边的程序框图,若输入的是100,则输出的变量S和T的值依次是( )
A. B. C. D.
3.已知一组抛物线,其中为2.4.6.8中任取的一个数,为1.3.5.7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线交点处的切线相互平行的概率是( )
A. B. C. D.
4.设e1,e2分别为具有公共焦点F1与F2的椭圆和双曲线的离心率,P为两曲线的一个公共点,且满足·=0,则的值为( )
A. B.1 C.2 D.不确定
5.把函数y=cos(x+)的图象向右平移φ个单位,所得到的图象正好是关于y轴对称,则φ的最小正值是 ( )
A. B. C. D.
6.如图,体积为V的大球内有4个小球,每个小球的球面过大球球心且与大球球面有且只有一个交点,4个小球的球心是以大球球心为中心的正方形的4个顶点.V1为小球相交部分(图中阴影部分)的体积,V2为大球内、小球外的图中黑色部分的体积,则下列关系中正确的是( )
A. B.
C. D.
7.如果执行右面的程序框图,那么输出的( )
A.2450 B.2500 21世纪教育网
C.2550 D.2652
8.设等比数列{}的前项和为 ,若=3 ,则 = ( )
A.2 B. C. D.3
9.若钝角三角形三内角的度数成等差数列,且最大边长与最小边长的比值为m,则m的范围是( )
A.(1,2) B.(2,+∞) C.[3,+∞ D.(3,+∞)
10. 如图, 正方体的棱线长为1,线段上有两个动点E,F,且,则下列结论中错误的是 ( )
A.
B.
C.三棱锥的体积为定值
D.异面直线所成的角为定值
第II卷
二、填空题
11.若为非零实数,则下列四个命题都成立:
① ② ③若,则
④若,则。则对于任意非零复数,上述命题仍然成立的序号是 。
12.设等差数列的前项和为,若,则的最大值为___________。
13.已知数列满足则的最小值为__________.
14.若关于x的不等式ax2一|x|+2a0的解集为,则实数。的取值范围为_________.
三、解答题(本大题共6小题,共0分)
15.如图,A1A是圆柱的母线,AB是圆柱底面圆的直径,C是底面圆周上异于A,B的任意一点,AA1=AB=2.
(1)求证:BC上平面A1AC; ︿
(2)求三棱锥A1一ABC的体积的最大值
16.已知函数,常数.
(1)当时,解不等式;
(2)讨论函数的奇偶性,并说明理由
17.
已知数列中, .
(Ⅰ)设,求数列的通项公式;
(Ⅱ)求使不等式成立的的取值范围.
18.设函数
(I)研究函数的单调性;
(II)比较与0的大小,并证明你的结论;
(III)判断关于x的方程的实数解的个数,并加以证明。
19.已知,点在函数的图象上,其中
⑴证明数列是等比数列;
⑵设,求及数列的通项;
⑶记,求数列的前项,并证明
20.已知梯形ABCD中,AD∥BC,∠ABC =∠BAD =,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点。沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) .
(1) 当x=2时,求证:BD⊥EG ;
(2) 若以F、B、C、D为顶点的三棱锥的体积记为f(x),求f(x)的最大值;
(3) 当 f(x)取得最大值时,求二面角D-BF-C的余弦值.
高二数学(理)答案
一、选择题
1.D??????2.D??????
解析:依据框图可得,
3.B??????
解析:这一组抛物线共条,从中任意抽取两条,共有种不同的方法.它们在与直线交点处的切线的斜率.若,有两种情形,从中取出两条,有种取法;若,有三种情形,从中取出两条,有种取法;若,有四种情形,从中取出两条,有种取法;若,有三种情形,从中取出两条,有种取法;若,有两种情形,从中取出两条,有种取法.由分类计数原理知任取两条切线平行的情形共有种,故所求概率为.本题是把关题.
4.C??????
解析:设a1 为椭圆的长半轴长,a2 为双曲线的实半轴长,当P点在双曲线的右支上时,由题意得,, |PF1 |=+,|PF2 |=-,由·=0,得 即PF1 PF2 , (+)2 +(一)2=4c2 ,? 22 +22 =4c2 , ? +=2,从而==+=2, ? 当P点在双曲线盯左支上时,解法同上,故选C
5.B??????6.D??????
解析:设大球半径为 ,小球半径为 根据题意所以 于是即所以,
7.C??????
解析:
8.B??????
解析:因为数列是等比数列,所以,,有,即,故.
9.B??????10.D??????
解析:A正确,易证B显然正确,;C正确,可用等积法求得;D错误。选D.
二、填空题
11.②④
12.4
13.
14.[,+∞)
三、解答题
15.解:(1) C是底面圆周上异于A、B的一点,且AB为底面圆的直径, ??? BCAC ??? AA1 平面ABC,BC平面ABC, ??? AA1 BC ??? AA1 AC=A,AA1 平面A1 AC,AC平面A1 AC, ??? BC平面A1 AC ? (2)解法一设AC=x,在Rt△ABC中,BC== (0x2), 故VA -ABC = S△ABC ·AA1 =××AC×BC × A A1 =x(0x2), 即VA -ABC =x== 0x2.0x2 4. ? 当x2 =2,即x=时,三棱锥A1 -ABC的体积取到最大值 解法二在Rt△ABC中,AC2 +BC2 =AB2 =4,VA -ABC = S△ABC ·AA1 =××AC×BC×A A1 =×AC×BC×=×= 当且仅当AC=BC时等号成立,此时AC=BC=:三棱锥A1 -ABC的体积的最大值为
16.解: (1), ????????????? ,????????????????? ????????????? .??????????????? ???? 原不等式的解为.????????? ??? (2)当时,, ??? 对任意,, ??? 为偶函数.? ??? 当时,, ??? 取,得 , ??? ,??? 函数既不是奇函数,也不是偶函数.
17.解: (Ⅰ), 所以是首项为,公比为4的等比数列, (Ⅱ) 用数学归纳法证明:当时. (ⅰ)当时,,命题成立; (ⅱ)设当n=k时,,则当n=k+1时, 故由(ⅰ)(ⅱ)知,当c>2时 当c>2时,令,由得 当 当时,,且 于是 当时, 因此不符合要求 所以c的取值范围是
18.解(I) 所以单调递减。 ?? (II)(解法1): ?? (解法2): ?? (III) ①当 ②当 综合单调递减。
19.(Ⅰ)由已知, ??? ,两边取对数得 ,即 是公比为2的等比数列. (Ⅱ)由(Ⅰ)知????????????? ?????????????????? (*) = 由(*)式得 (Ⅲ),, 又, ,??? 又???? .
20. 解:(1)(法一)∵平面平面,AE⊥EF,∴AE⊥面,AE⊥EF,AE⊥BE,又BE⊥EF,故可如图建立空间坐标系E-xyz。 则A(0,0,2),B(2,0,0),G(2,2,0),D(0,2,2),E(0,0,0) (-2,2,2),(2,2,0) (-2,2,2)·(2,2,0)=0,∴ (法二)作DH⊥EF于H,连BH,GH, 由平面平面知:DH⊥平面EBCF, 而EG平面EBCF,故EG⊥DH。 又四边形BGHE为正方形,∴EG⊥BH, BHDH=H,故EG⊥平面DBH, 而BD平面DBH,∴ EG⊥BD。 (或者直接利用三垂线定理得出结果) (2)∵AD∥面BFC, 所以 VA-BFC ==··4·(4-x)·x 即时有最大值为。 (3)(法一)设平面DBF的法向量为, ∵AE=2, B(2,0,0),D(0,2,2), F(0,3,0),∴(-2,2,2), 则 , 即, 取x=3,则y=2,z=1,∴? 面BCF的一个法向量为 则cos<>= 由于所求二面角D-BF-C的平面角为钝角, 所以此二面角的余弦值为-?? (法二)作DH⊥EF于H,作HM⊥BF,连DM。 由三垂线定理知 BF⊥DM,∴∠DMH是二面角D-BF-C的平面角的补角。 由△HMF∽△EBF,知,而HF=1,BE=2,, ∴HM=。? 又DH=2, ∴在Rt△HMD中,tan∠DMH=-,21世纪教育网 因∠DMH为锐角,∴cos∠DMH=, 而∠DMH是二面角D-BF-C的平面角的补角, 故二面角D-BF-C的余弦值为-。21世纪教育网
同课章节目录
